Пример 3
Для
нижеприведенной схемы электроснабжения
(рис. 10) записать события, заключающиеся
в работоспособности RC
и отказе
системы, обозначая состояния
работоспособности и отказа элементов
буквами Ri
и
i
соответственно.
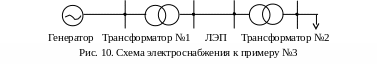Решение.
Для описания состояния системы сначала
составляется полная фраза, описывающая
это состояние (обычно достаточно сделать
это устно): работоспособность системы
Rс
заключается в работоспособности всех
её элементов. Сформулирована эта фраза
должна быть так, чтобы в ней присутствовали
ключевые слова – союзы И и ИЛИ: Система
работоспособна, когда работоспособен
«И» генератор RГ,
«И» первый трансформатор RТ1,
«И» линия RЛ,
«И» второй трансформатор RТ2.
Так как союз «и» является признаком
произведения событий, записываем: Rс
= RГ
RТ1
RЛ
RТ2
.
Система неработоспособна С, если отказал генератор Г, «ИЛИ» отказал первый трансформатор Т1, «ИЛИ» отказала линия Л, «ИЛИ» отказал второй трансформатор Т2, «ИЛИ» произошел отказ любой пары элементов схемы, ИЛИ любой тройки, «ИЛИ» отказали все четыре элемента. Так как союз «или» является признаком суммы событий, записываем: С = Г + Т1 + Л + Т2 .
Следует обратить внимание, что добавлять в окончательное выражение для С произведения отказов, взятые парами, тройками или четверкой не нужно, так как это приведёт к тавтологии – понятие суммы для четырёх событий уже включает в себя появление событий, взятых по одному, по два, по три или сразу всех вместе.
Пример
4
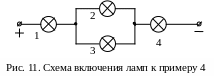
Для схемы включения электрических ламп (рис. 11) записать выражения: «в цепи протекает ток» - Rс, «ток в цепи не протекает» - С, обозначая состояния работоспособности и отказа ламп буквами RЛi и Лi соответственно.
Решение. Ток в цепи будет протекать (т. е. система будет работоспособна - Rс), когда будут работоспособны первая R1 «И» четвертая R4 лампы «И» хотя бы одна (любая) из двух оставшихся, т.е. «ИЛИ» вторая R2, «ИЛИ» третья R3, «ИЛИ» вторая «И» третья совместно: RС = R1R4(R2 + R3).
Тока в цепи не будет С, если откажет «ИЛИ» первая лампа 1, «ИЛИ» четвертая 4, «ИЛИ» вторая 2 «И» третья 3 совместно, «ИЛИ» откажут совместно любые три «ИЛИ» все четыре лампы: C = 1 + 4 + 2 3 .
Из рассмотренных примеров видно, что для безошибочного решения подобных задач необходимо сначала устно с использованием союзов И, ИЛИ сформулировать интересующее событие, а затем кратко записать его с использованием понятий алгебры событий и выбранных обозначений.
Логические схемы анализа надежности
Пример 5
Система состоит из трех независимо работающих элементов. Записать выражения для состояний RС и С, если известно, что она отказывает при отказе любого элемента (примером такой системы является автомобиль, который можно считать состоящим из трёх независимо работающих элементов – двигателя, ходовой части и водителя, – отказ любого из них приводит к отказу системы).
Решение. Следуя рассуждениям, приведённым в примерах 3 и 4 можно записать:
Rс = R1 R2 R3 ; с = 1 + 2 + 3.
Сравнение этих выражений с выражениями, записанными в примере №3, показывает их полную идентичность. Это свидетельствует о том, что систему, о которой идёт речь в рассматриваемой задаче, можно представить в виде простейшей электрической цепи из трёх последовательно соединённых элементов, иначе говоря, в виде логической схемы анализа надёжности.
Логической схемой анализа надёжности называется схема, в которой реальные объекты и составляющие их элементы с целью облегчения анализа надежности представляются в виде простейшей электрической цепи. На логических схемах реальные элементы заменяются сопротивлениями, включенными в электрическую цепь. Логическая схема отображает не фактические взаимосвязи элементов (механические, электрические и пр.), а только их функциональные взаимосвязи, то есть показывает, как состояние отдельных элементов системы влияет на состояние системы в целом.
Анализ надёжности при использовании логической схемы сводится к решению вопроса, при каких состояниях элементов в цепи будет (или, наоборот, не будет) протекать ток.
Элементы на логической схеме соединяются
последовательно, если отказ любого из них приводит к отказу системы;
параллельно, если система отказывает при отказе всех элементов.