Характеристики «скошенности» и «островершинности» закона распределения случайных величин
Третий
центральный момент
служит для характеристики асимметрии
«скошенности» распределения. Он имеет
размерность куба случайной величины;
чтобы получить безразмерную характеристику
и «отстроиться» от одновременной оценки
разброса третий момент делят на куб
среднего квадратического отклонения.
Полученная величина называется
коэффициентом «скошенности»:
.
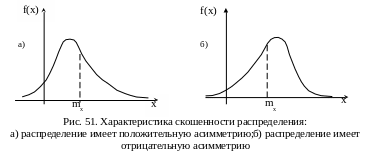При положительной асимметрии (рис. 51)
более пологая и длинная часть кривой
распределения располагается справа от
математического ожидания, а при
отрицательной (рис. 52) – слева.
Четвертый
центральный момент
служит для характеристики островершинности
и плосковершинности
кривой распределения. Эти свойства
описываются с помощью коэффициента
эксцесса:
Для нормального закона распределения (закона Гаусса) Ех = 0.
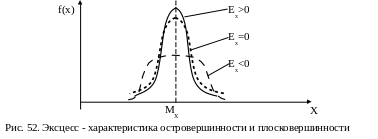Кривые, островершинные по сравнению
с нормальным законом распределения,
обладают положительным эксцессом,
плосковершинные – отрицательным (рис.
52).
Литература
1. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения. М.: Высшая школа, 2005, - 480 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшее образование., 2006, - 576 с.
3. Вентцель Е.С. Теория вероятностей. М.: Высш. шк., 2006. - 576 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. шк., 2006. - 404 с.
5. Письменный Д. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. - М.: Айрис-пресс, 2006. – 288 с.
6. Гнеденко Б.В. Курс теории вероятностей. – М.: Едиториал УРСС, 2005. – 448 с.
Оглавление
Введение. Значение дисциплины для инженеров-электриков 4
Предмет теории вероятности. Краткая история её развития 5
1. Классическая формула определения вероятности события 16
2. Геометрическая формула определения вероятности события 17
3. Статистическая формула определения вероятности события 19
4. Условная вероятность события 21
Формулы умножения вероятностей 22
2. Формулы сложения вероятностей 24
3. Определение вероятности хотя бы одного события 27
4. Формула полной вероятности 29
5. Формула Бейеса (теорема гипотез) 30
6. Формула Бернулли (частная теорема о повторении опытов) 32
Ряды распределения СВ 35
Интегральная функция распределения вероятностей случайной величины 38
Плотность распределения вероятностей случайной величины и гистограмма 44
Мода и медиана случайной величины 47
Математическое ожидание СВ и его свойства 49
Моменты СВ как характеристики различных свойств этих величин 52
Дисперсия случайной величины - характеристика разброса (рассеивания) значений случайной величины около центра распределения 53
Характеристики «скошенности» и «островершинности» закона распределения случайных величин 55