Невырожденные матрицы
Пусть дана
-
квадратная матрица
-
порядка
,
ОПРЕДЕЛЕНИЕ: Квадратная матрица называется невырожденной, если ее определитель не равен 0.В противном случае матрица вырожденная.
ОПРЕДЕЛЕНИЕ:
Матрицей,
союзной к матрице
называется матрица
,
имеющая следующий вид:
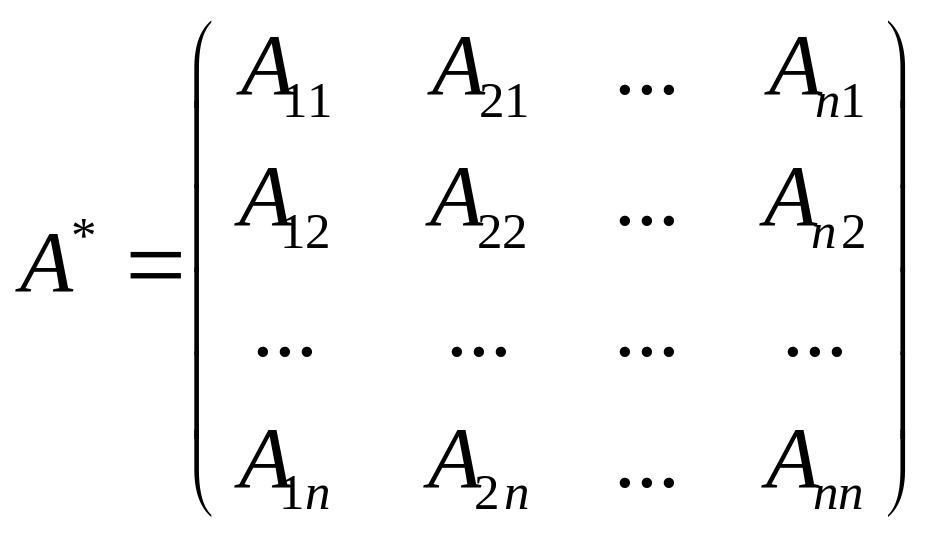
где
-
алгебраические дополнения элемента
данной матрицы, который определяется
также как алгебраическое дополнение
элементов определителя.
ОПРЕДЕЛЕНИЕ:
Матрица
называется обратной к матрице
,
если выполняется условие
имеет те же размеры, что и .
Обратная матрица
ТЕОРЕМА: Всякая невырожденная матрица имеет обратную.
Принимаем без доказательства.
Свойства обратной матрицы:
1)
;
2)
;
3)
.
4) Если матрица имеет обратную, то эта обратная матрица единственная
5)
,
если
.
Ранг матрицы
Пусть дана
матрица, имеющая
строк и
столбцов. Вычеркнем из этой матрицы
некоторые строки и столбцы так, чтобы
число оставшихся строк и столбцов стало
одинаково, например,
.
Составим определитель из них. Этот
определитель называется минором
-го
порядка. Количество таких миноров
определяется числами
и
,
а наивысший порядок, который они могут
иметь, равен наименьшему из двух чисел
и
.
Наименьший порядок этих определителей равен 1, причем определители 1 порядка суть сами элементы матрицы.
ОПРЕДЕЛЕНИЕ:
Рангом
матрицы называется наивысший порядок
отличных от нуля миноров. Обозначается
или
.
Если ранг матрицы
есть
,
то среди определителей порядка
,
входящих в эту матрицу, есть, по крайней
мере, 1, отличный от нуля, но все определители
порядка
равны нулю.
Примеры:
Определить ранг матрицы
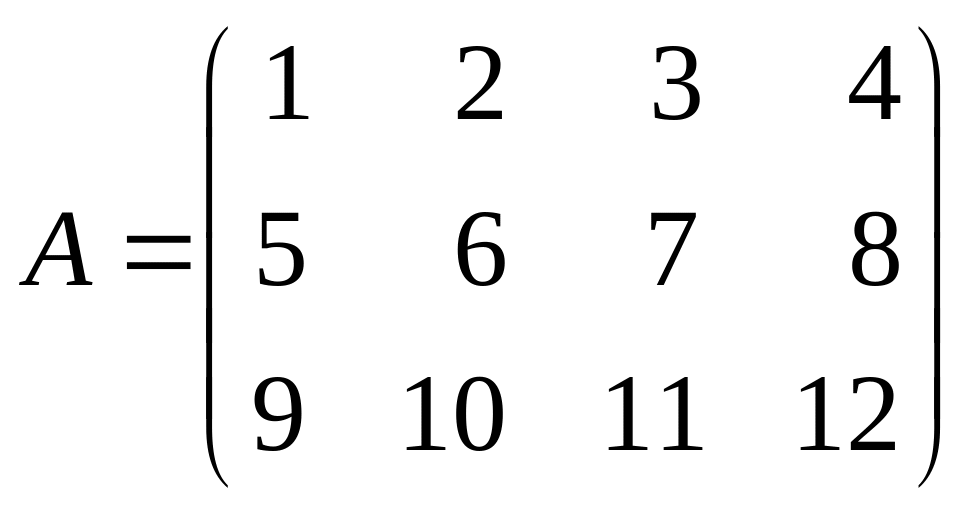
Матрица
прямоугольная
.
Наивысший порядок определителей, входящих в данную матрицу, равен 3.Эти определители могут быть получены только вычеркиванием одного столбца. Найдем их:
;
;
;
,
все определители 3 порядка равны 0,
следовательно
.
Переходим к рассмотрению определителей
2 порядка: Вычеркнем, например, 3-ю строку
и 3-й и 4-й столбец, тогда имеем определитель
.
Следовательно, высший порядок отличных
от нуля определителей, входящих в
матрицу, есть 2, а потому
.