Свойства операции транспонирования:

1) 2)

3) 4)

ОПРЕДЕЛЕНИЕ: Квадратная матрица называется симметричной, если ее элементы симметричные относительно главной диагонали равны между собой:

Для симметричных матриц выполняются следующие свойства операции транспонирования:

1)

2) Для любой матрицы , матрицы и симметричны.

Определители

Необходимость введения определителя – числа, характеризующего квадратную матрицу , тесно связано с решением систем линейных уравнений, (которые мы будем изучать, и рассматривать на следующей лекции). А пока введем данное понятие.

Определитель-это число, которое ставится в соответствие любой квадратной матрице.

1. Определителем 1-го порядка матрицы , называется элемент , т.е. . Пусть 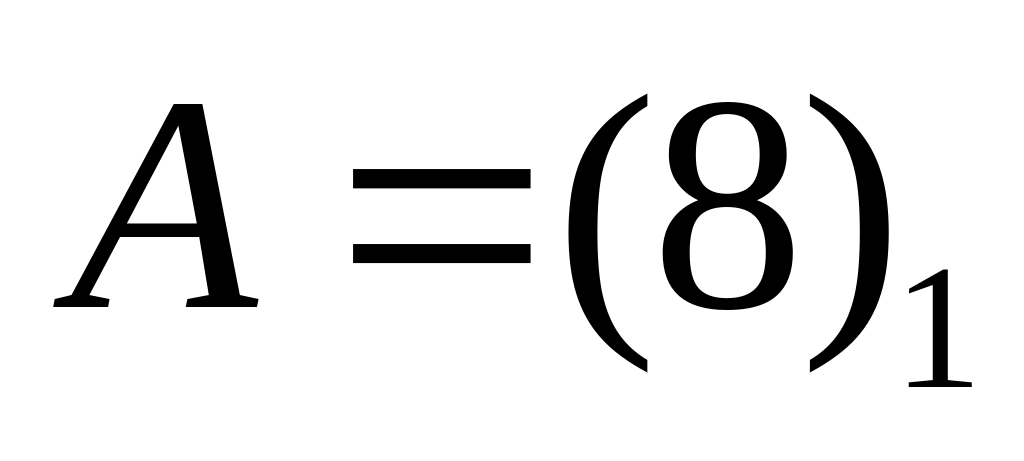тогда .

2. Определителем 2-го порядка матрицы , называется число, которое вычисляется по формуле:

.

Пример: Дана , найти ?

3. Определителем 3-го порядка матрицы 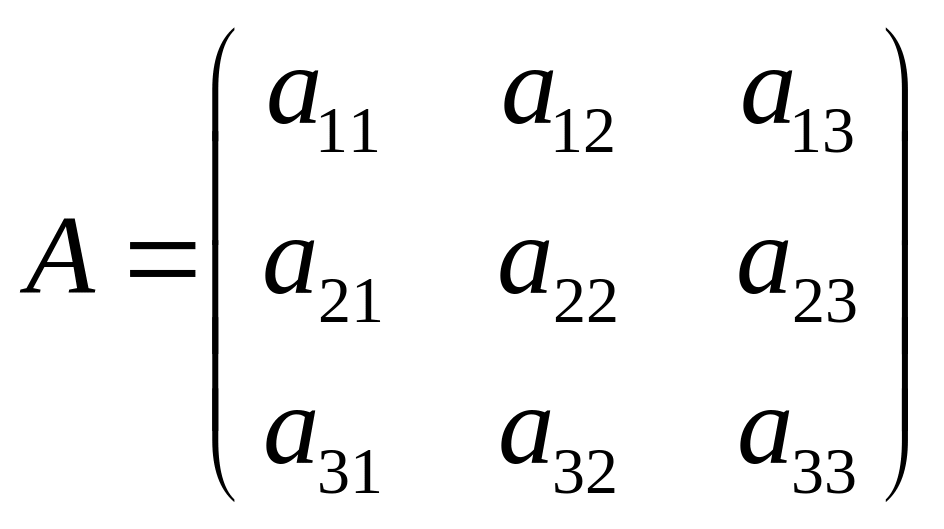, называется число, которое вычисляется по формуле:

.

Это правило называется правилом САРРЮСА

ПРИМЕР: , найти .

.

Правило вычисления определителей матриц порядка является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителей по элементам некоторого ряда. Его мы рассмотрим дальше в свойствах определителей.

Свойства определителей

1. «Равноправность строк и столбцов»

Определитель не изменится, если его строки заменить столбцами, и наоборот.

В дальнейшем строки и столбцы будем называть рядами определителя.

2) При перестановке 2-х параллельных рядов определитель меняет свой знак.

3) Определитель, имеющий два одинаковых ряда, равен 0.

4) Общий множитель элементов какого-либо ряда можно вынести за знак определителя.

ЗАМЕЧАНИЕ: Из свойств 3) и 4) следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда , то такой определитель равен нулю.

5)Если элементы какого-либо ряда определителя представляют собой суммы 2-х слагаемых, то определитель должен быть разложен на сумму двух соответствующих определителей.

6) Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы другого ряда, умноженные на любое число

.

поскольку 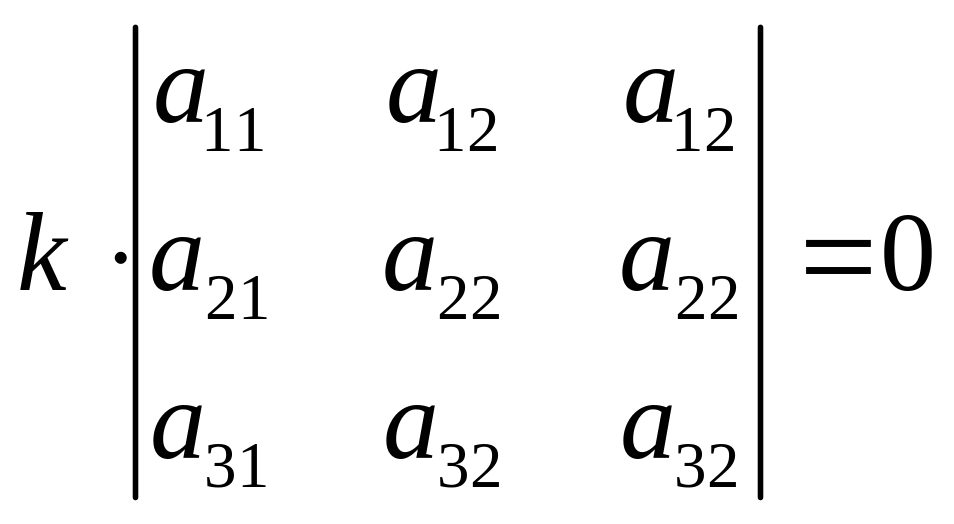, т.к. имеет два одинаковых ряда.

Дальнейшие свойства связаны с понятием минора и алгебраического дополнения. Введем эти понятия.

ОПРЕДЕЛЕНИЕ: Минором некоторого элемента определителя - порядка называется определитель - порядка, полученный из исходного, путем вычеркивания строки и столбца, на пересечении которых находится данный элемент. Обозначается .

Так если

, то 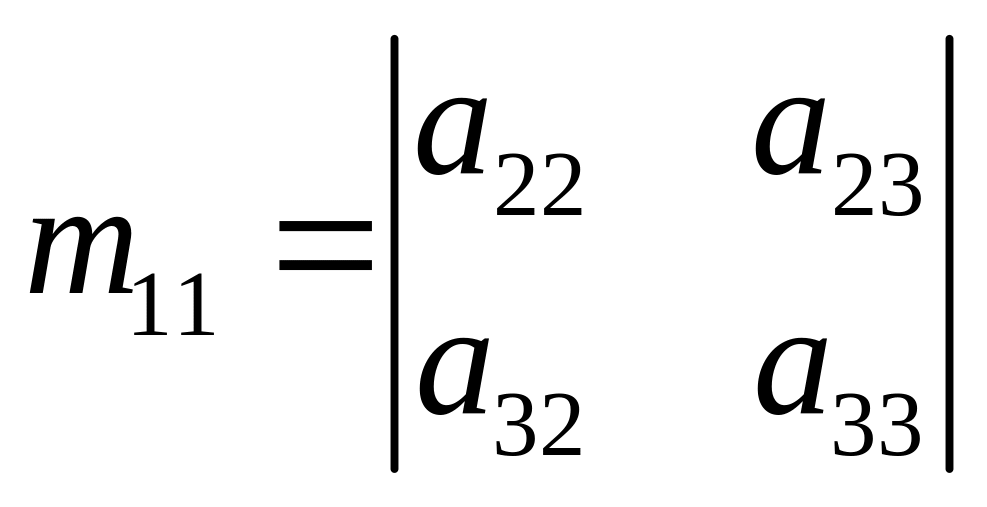, , 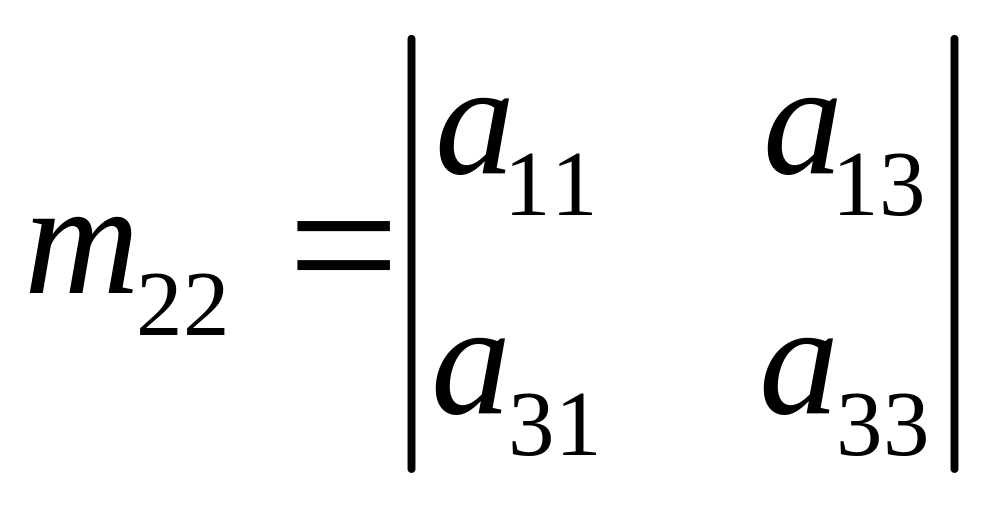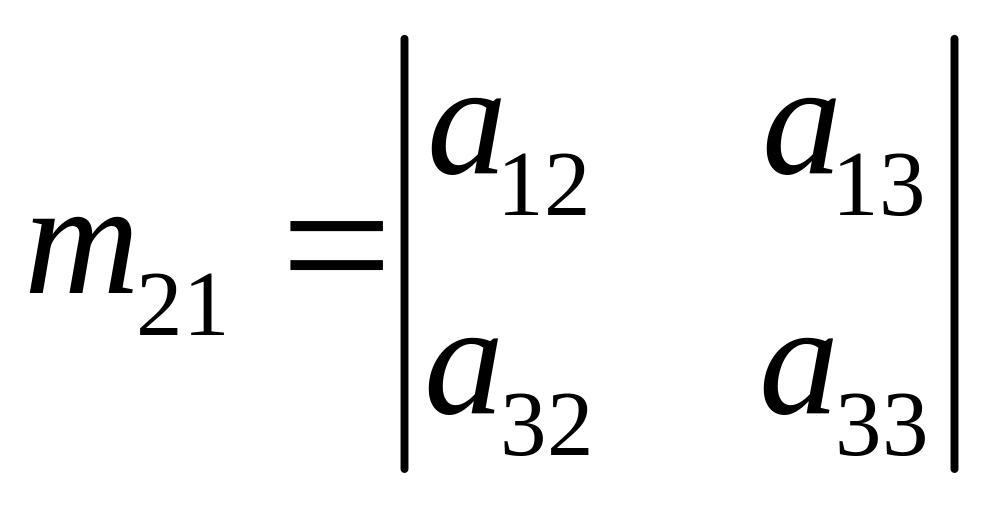и т.д.

ОПРЕДЕЛЕНИЕ: Алгебраическим дополнением элемента называется его минор, взятый со знаком +, если сумма - четное число, и - если - нечетное число.

Так

Теперь сформулируем последнее свойство определителей, которое известно как теорема Лапласа.

ТЕОРЕМА: Определитель равен сумме произведений элементов какого-либо ряда на соответствующие им алгебраические дополнения.

- разложение по элементам - строки

- разложение по элементам - столбца

.

Без доказательства.

Значение теоремы Лапласа заключается в том, что она позволяет свести определитель - порядка к определителю - порядка.

ПРИМЕР: Найти определитель матрицы .

РЕШЕНИЕ: Воспользуемся теоремой Лапласа, разложим определитель по элементам 1 строки