
- •Матрицы
- •Действия над матрицами
- •1.Умножение матрицы на число
- •2. Сложение матриц.
- •3. Вычитание матриц.
- •4. Умножение матриц
- •5. Возведение в степень
- •6. Транспонирование матрицы
- •Свойства операции транспонирования:
- •Определители
- •Свойства определителей
- •Невырожденные матрицы
- •Обратная матрица
- •Свойства обратной матрицы:
- •Ранг матрицы
Лекция №4 « Матрицы и определители»
Матрицы
ОПРЕДЕЛЕНИЕ:
Матрицей размера
![]() называется прямоугольная красивая
таблица чисел, содержащая
называется прямоугольная красивая
таблица чисел, содержащая
![]() строк и
строк и
![]() столбцов.
столбцов.
Для обозначения
матриц применяются круглые скобки
![]() ,
квадратные скобки
,
квадратные скобки
![]() или двойные вертикальные черточки
или двойные вертикальные черточки
![]() .
.
ПРИМЕРЫ: Таблицы чисел
![]() ,
,
![]() ,
,
![]() ,
,
![]()
представляют собой матрицы.
Таблицы
 ,
,
![]() ,
,
![]()
не являются матрицами, поскольку они не прямоугольны.
Матрицы, в отличие
от определителя, не являются числом.
Это условный способ обозначения таблиц
с числами. Матрицы обычно обозначаются
большими латинскими буквами
![]() …..
…..
Запишем матрицу, имеющую строк и столбцов:
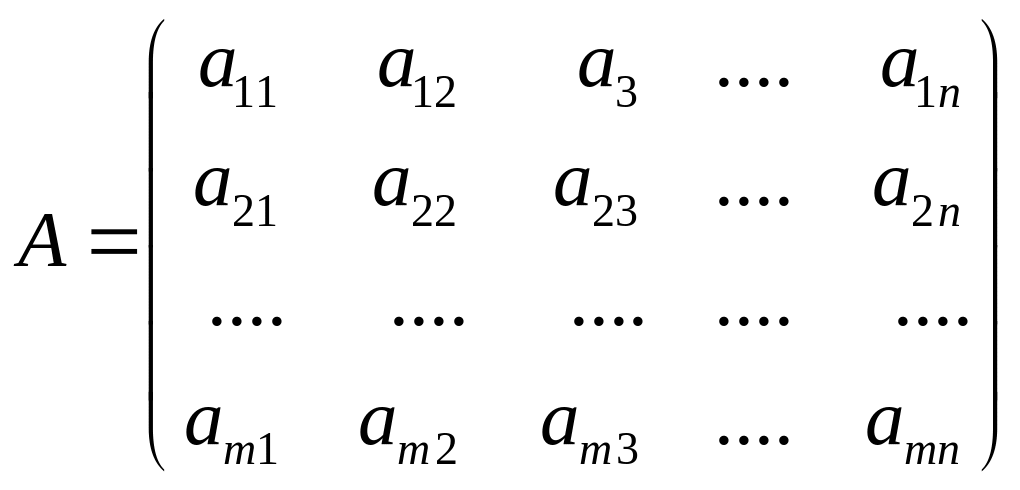 (1)
(1)
Числа
![]() ,
составляющие
матрицу, (
-
номер строки,
-
номер столбца)
называются
элементами
матрицы.
,
составляющие
матрицу, (
-
номер строки,
-
номер столбца)
называются
элементами
матрицы.
В сокращенной
записи (1) выглядит так:
![]() .
.
Если матрица имеет одинаковое число строк и столбцов, она называется квадратной, или матрицей - порядка.

Элементы,
![]() стоящие на диагонали, идущей из левого
верхнего угла в правый нижний, образуют
главную
диагональ.
стоящие на диагонали, идущей из левого
верхнего угла в правый нижний, образуют
главную
диагональ.
А элементы
![]() образуют побочную
диагональ.
образуют побочную
диагональ.
Матрица, все элементы которой нули, называется нулевой матрицей.
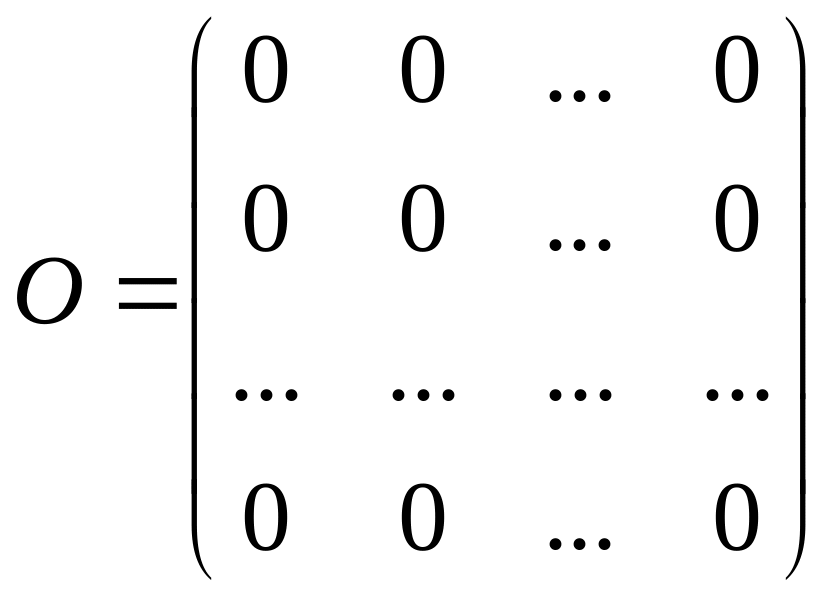
ОПРЕДЕЛЕНИЕ: Квадратная матрица, у которой все элементы, кроме элементов на главной диагонали равны 0, называется диагональной.
ОПРЕДЕЛЕНИЕ: Диагональная матрица, у которой каждый элемент на главной диагонали равен 1, называется единичной.
Обозначают
![]() .
.
ПРИМЕРЫ:
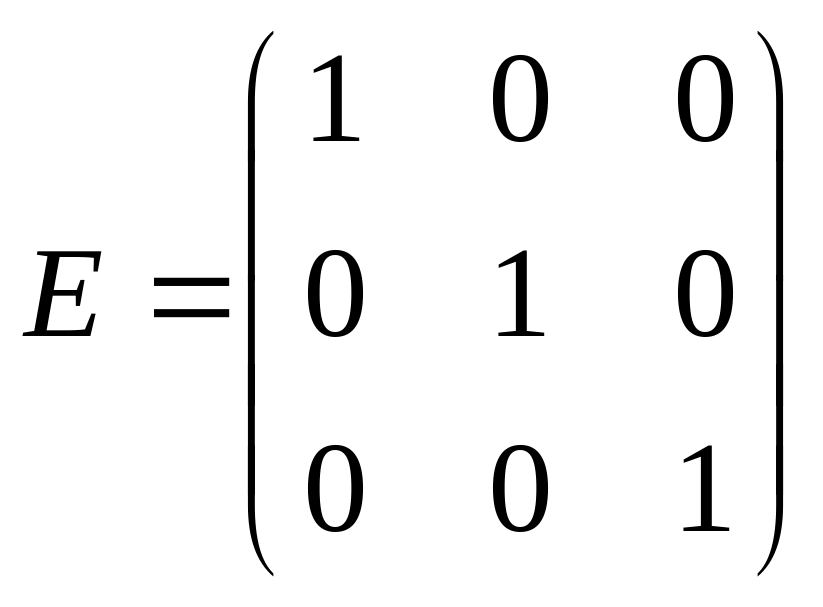 - единичная
матрица 3 порядка;
- единичная
матрица 3 порядка;
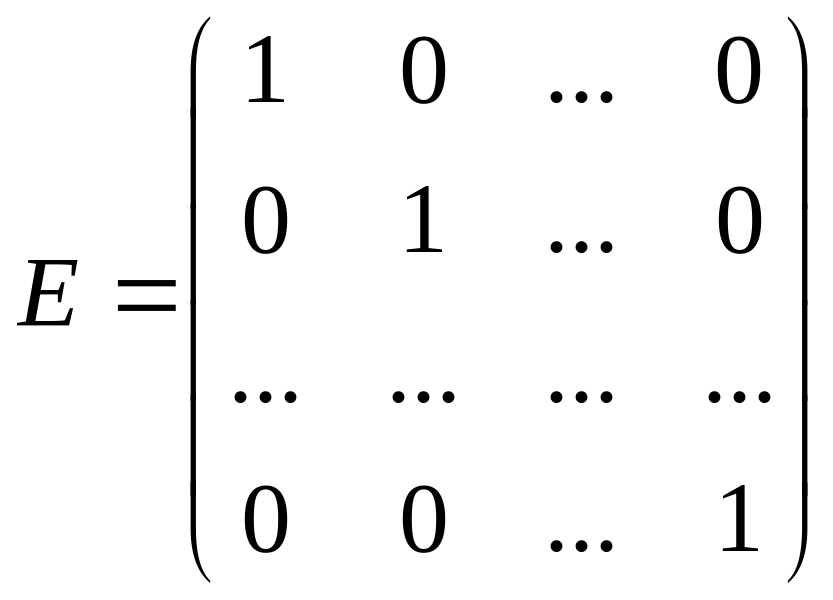 -
единичная
матрица
- порядка
-
единичная
матрица
- порядка
ОПРЕДЕЛЕНИЕ: Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали равны 0.
ЗАМЕЧАНИЕ:
В матричном исчислении матрицы
![]() играют такую же роль как 0 и 1 в арифметике.
Т.е это 2 нейтрали для операций сложения
(0) и операции умножения (
).
играют такую же роль как 0 и 1 в арифметике.
Т.е это 2 нейтрали для операций сложения
(0) и операции умножения (
).
При умножении
матрицы
![]() на единичную матрицу
того же размера, получаем исходную
матрицу
.
на единичную матрицу
того же размера, получаем исходную
матрицу
.
При сложении
матрицы
и нуль матрицы
![]() ,
в результате получаем матрицу
,
,
в результате получаем матрицу
,
ОПРЕДЕЛЕНИЕ: Матрица, содержащая 1 столбец или одну строку, называется вектор столбец (матрица-столбец) или вектор строка (матрица-строка).
 или
или
![]()
Матрица может
состоять из одного числа, например 7,
она отождествляется с этим числом, т.е.
![]() есть число 7 в обычном понимании.
есть число 7 в обычном понимании.
ОПРЕДЕЛЕНИЕ:
Две матрицы
и
![]() называются равными
называются равными
![]() ,
если они одинакового размера (т.е. имеют
одинаковое число строк и одинаковое
число столбцов) и их соответствующие
элементы равны.
,
если они одинакового размера (т.е. имеют
одинаковое число строк и одинаковое
число столбцов) и их соответствующие
элементы равны.
Если
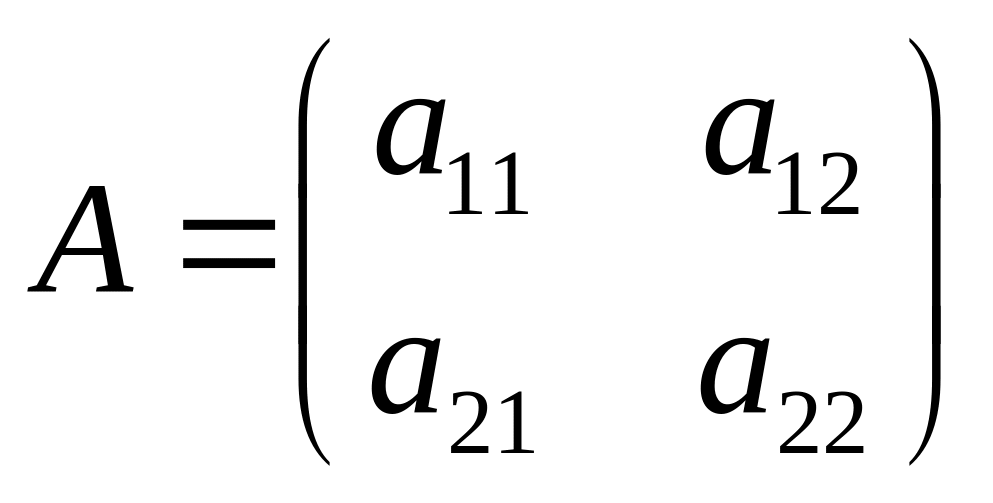 и
и
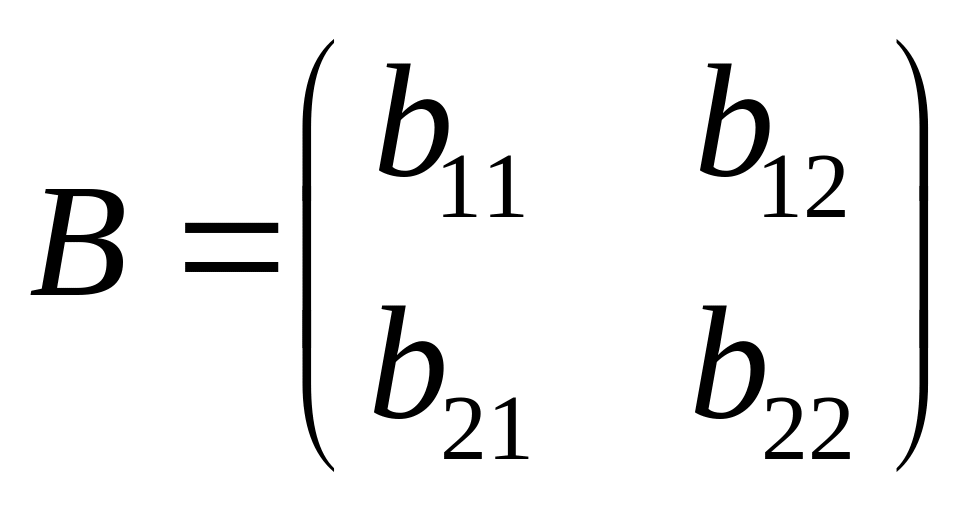 ,
то
,
когда
,
то
,
когда
![]()
Действия над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.
1.Умножение матрицы на число
ОПРЕДЕЛЕНИЕ:
Произведением матрицы
на число
![]() называется матрица
называется матрица
![]() ,
элементы которой
,
элементы которой
![]() для
для
![]() ;
;
![]() .
.
ПРИМЕР:
если
![]() ,
то
,
то
![]() ;
;
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы
![]() ;
;
В частности произведение матрицы на число 0 есть нулевая матрица, т.е
![]() где
где
![]() размер нулевой матрица зависит от
размера
.
размер нулевой матрица зависит от
размера
.
