6.3. Функциональное преобразование векторных случайных процессов
Часто в практике встречаются векторные
случайные процессы, когда
в каждый момент времени
t
случайные процессы описываются
несколькими
случайными величинами:
(например, сигнал в двух каналах
стереофонического магнитофона,
огибающая и фаза сигнала, два цветоразностных
сигнала
в цветном телевидении, множество
сигналов записываемых на бортовой
регистратор и т.д.).
Пусть случайные величины
и
связаны функциональными
преобразованиями:
....................................
В
том случае, если существуют однозначные
обратные функции:
то плотность распределения вероятности
векторной случайной величины
определяется выражением:
где
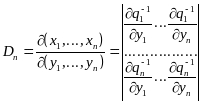(6.1)
- якобиан преобразования.
Если функции
неоднозначны, то тогда надо взять суммы
функций по всем областям.
6.4. Узкополосные случайные процессы
Для эргодических случайных процессов
при равенстве матожидания нулю случайному
процессу
с помощью преобразования Гильберта
можно поставить в соответствие новый
сопряженный с ним
стационарный случайный процесс
Случайный процесс и ему сопряженный можно записать в виде:
где
- огибающая;
- фаза случайного процесса.
A(t)
и
Ф(t)
обладают следующими свойствами:
в каждый момент времени
выполняется
неравенство
и поэтому случайная функция
не
пересекает огибающую
A(t).
Кроме того,
и поэтому в тех точках, где
имеется равенство
,
т.е. функции
и
не пересекаются и в точках соприкосновения
имеют общие касательные. Это объясняет
смысл названия
.
Таким образом, при таком представлении
случайный процесс
можно считать гармоническим колебанием,
модулированным по амплитуде и фазе
случайными функциями
и
.
Если случайный процесс
- нормальный, то нормальным будет и
сопряженный процесс
(так как преобразование Гильберта
является линейным). Пусть
спектральная плотность конкретной
реализации
,
тогда спектр сопряженной реализации
.
Модули спектральных плотностей совпадают,
поэтому одинаковы и спектральные
плотности процессов
и
,
и корреляционные функции
Здесь
- односторонний спектр мощности
.
Взаимная корреляционная функция сопряженных процессов
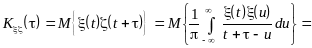
Таким образом, взаимная корреляционная
функция
и корреляционная функция
являются парой преобразования Гильберта.
Можно показать, что
=-
.
Следовательно, находя корреляционную функцию через энергетический спектр, получаем:
где
- обозначает преобразование Гильберта.
Отсюда следует, что взаимная корреляционная
функция сопряженных процессов нечетная
,
если, то
,
следовательно, процессы
и
- некогерентны, а если процессы нормальные,
то они и независимы.
Рис.
6.5. Энергетический спектр узкополосного
процесса
,
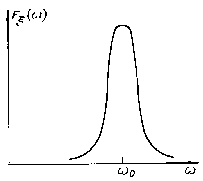
не равной нулю (рис. 6.5.). По теореме
Винера-Хинчина найдем корреляционную
функцию узкополосного процесса:
где
.
Поскольку процесс узкополосный, то при
,
поэтому можно считать, что с пренебрежимо
малой погрешностью
Или
где
Если спектр мощности
симметричен относительно частоты
,
то
и следовательно,
где
- квадрат среднеквадратического
отклонения;
- нормированная огибающая корреляционной
функции.
Для узкополосного процесса полезным является квазигармоническое представление
здесь огибающая U(t)
и начальная фаза
представляют собой медленно
изменяющиеся случайные функции
времени. Можно представить
как сумму
синфазной и квадратурных
составляющих:
где
и
медленно изменяющиеся функции времени
с низкочастотным
спектром.
Сопряженный процесс
можно найти с помощью преобразования
Гильберта.
Поскольку функции
и
медленные, их можно (с небольшой
погрешностью)
считать постоянными и вынести
за знак интеграла. Тогда:
Для узкополосного случайного процесса взаимная корреляционная функция с сопряженным процессом
