7

Международный университет природы, общества и человека

«ДУБНА»

Кафедра общей физики

Лабораторная работа №1

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ

ТВЁРДЫХ ТЕЛ

Разработал: д.т.н. Гребёнкин М.Ф.

г. Дмитров

2003

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ

Цель работы:

1. Научиться пользоваться измерительными инструментами (масштабной линейкой, штангенциркулем и микрометром).

2. Экспериментально определить плотность твердых тел разной геометрической формы.

3. Освоить методы обработки результатов измерений.

Приборы и принадлежности:

Набор из двух тел различной геометрической формы, масштабная линейка, штангенциркуль, микрометр, весы.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Плотностью однородного вещества называют физическую величину, определяемую отношением массы вещества m к занимаемому ею объему V

/1/

В неоднородных веществах (телах) плотность различных участков различна. Поэтому выбирают достаточно малый объем вещества, в пределах которого вещество можно считать однородным. Тогда

/2/

где – масса вещества в объеме .

В пределе /3/

Плотность вещества зависит от температуры, так как объем, занимаемый веществом, является функцией температуры. Поэтому при определении плотности вещества нужно указать, при какой температуре выполнены измерения.

Так как в лабораторной работе используются тела из однородного вещества, то при определении плотности можно воспользоваться формулой /1/.

Масса тела обычно определяется взвешиванием на весах¹.

Определение объема тела правильной геометрической формы может быть выполнено путем измерения характерных линейных размеров. Так, для определения объема шара

/4/

нужно измерить диаметр шара.

Для других тел, которые можно использовать в работе, аналогичными формулами являются:

1. Для круглого прямого конуса 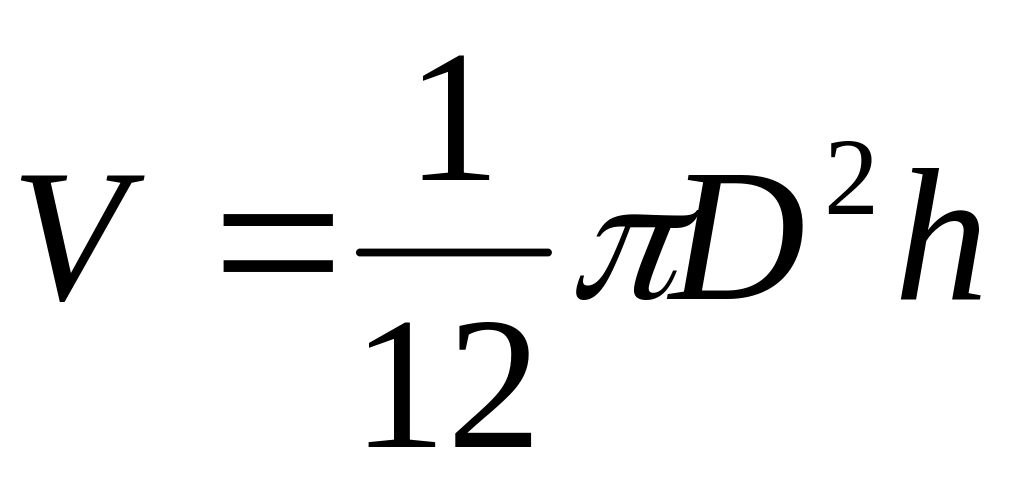/5/

2. Для круглого прямого цилиндра 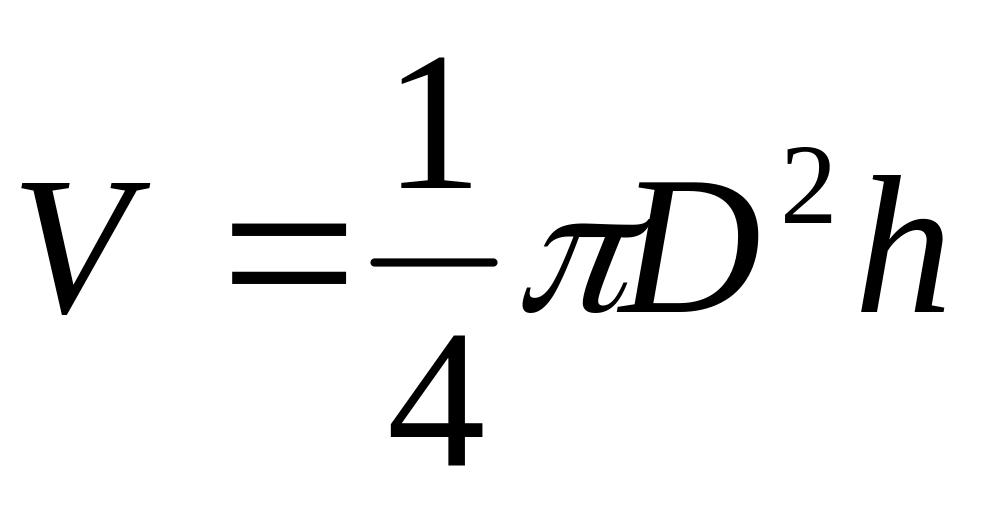/6/

3. Для цилиндрической трубы /7/

4. Для правильной прямой шестигранной призмы 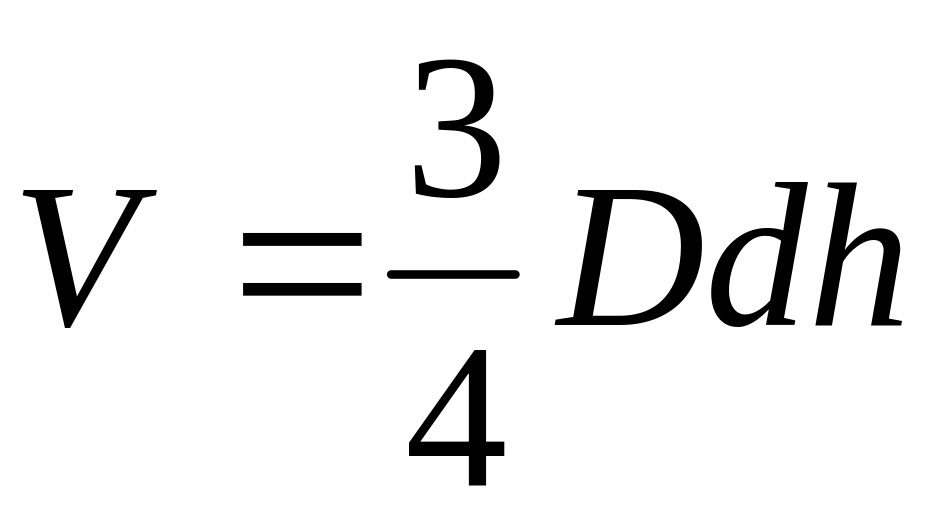, /8/

где

- диаметр описанной окружности;

- диаметр вписанной окружности;

- высота призмы.

Для определения линейных размеров тел пользуются измерительными инструментами. В настоящей работе измерения выполняются при помощи масштабной линейки, штангенциркуля и микрометра.

2. Измерение при помощи штангенциркуля

Простейшим измерительным прибором является масштабная линейка. Величина наименьшего деления такой линейки обычно равна 1 мм = 10^-3 м. Ее называют ценой деления. Такой линейкой можно произвести измерения линейных размеров с погрешностью ± 0,5 мм. При измерении малых (порядка 20÷30 мм) линейных размеров требуется большая точность. С этой целью вместе с масштабной линейкой пользуются вспомогательной шкалой – линейным нониусом, с помощью которого более точно можно отсчитывать доли самого малого деления основной шкалы. На рис. 1 условно показаны нониус N и масштабная линейка M.

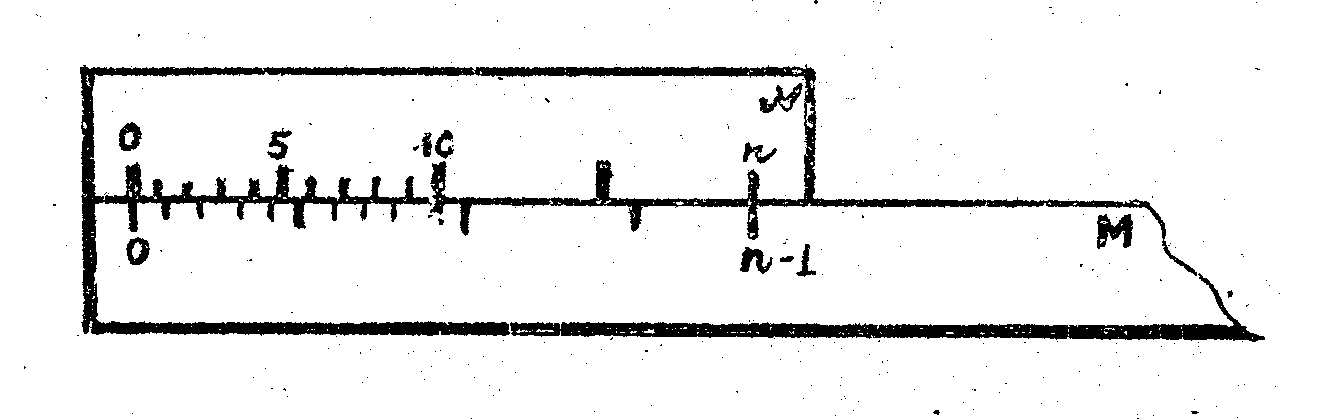
Рис. 1

Линейный конус N представляет собой небольшую линейку с делениями, которая может перемещаться вдоль основного масштаба (М). Шкала нониуса содержит n делений (рис. 1). Причем, по конструкции длина нониуса подбирается так, чтобы делений его шкалы составляло делений основного масштаба.

Если цена деления шкалы нониуса , а цена деления линейки основного масштаба , то очевидно, что или

/10/

и разность между ценой деления масштаба и нониуса равна

/11/

Формула /11/ дает выражение точности нониуса. Из /11/ видно, что определяется ценой деления масштаба и числом делений нониуса.

В таблице 1 приведены наиболее часто встречающиеся нониусы с миллиметровой масштабной линейкой.

Табл. 1

Цена деления масштаба в мм	1	1	1	0,5
Число делений нониуса	10	20	50	25
Точность нониуса в мм	0,1	0,05	0,02	0,02

Рассмотрим процесс измерения при помощи линейного нониуса. Пусть – измеряемый отрезок. Совместим с его началом нулевое деление начального масштаба. Пусть при этом конец его окажется между и делениями этого масштаба. Тогда можно написать

/12/

где - какая-то доля -го деления масштаба.

Для определения используется нониус (рис. 2).

Пусть K-е деление нониуса ближе всего совместится с делением масштаба. Тогда длина тела будет равна

/13/

где .

Учтя /11/, получим окончательно

, /14/

т. е. длина тела определяется числом целых делений, отсчитанных по шкале до нулевого деления нониуса, и делением нониуса, совпадающим с одним из делений масштаба.

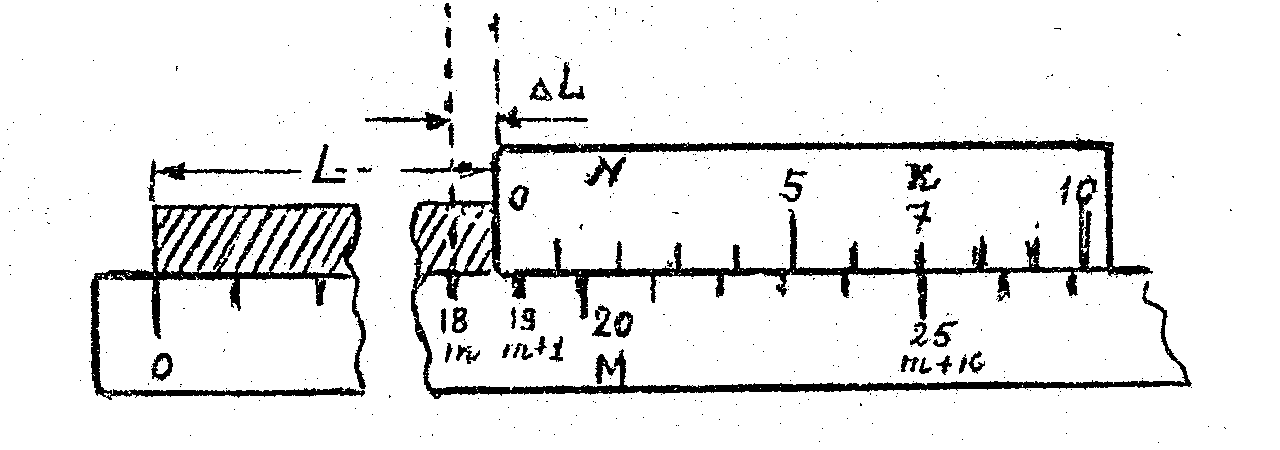На рис. 2 показан случай, когда правый конец тела расположен между 18 и 19 делениями масштаба, а 7-е деление нониуса совпадает (ближе всего) с 25 делением масштаба.

Рис. 2

Длина же равна при n = 10

,

при мм получим мм.

Погрешность, возникающая при таком методе отсчета, обусловлена неточным совпадением k-го деления нониуса с делением масштаба, и величина ее не будет превышать (1/2) , т. к. при больших несовпадениях этих меток отсчет будет производиться по другим делениям. Следовательно, можно принять, что погрешность при измерениях с помощью нониуса равна · . На рис. 3 изображен штангенциркуль – прибор, сочетающий масштабную линейку 1 с подвижным нониусом 2. При помощи штангенциркуля можно произвести измерения A – внешних размеров; В – внутренних размеров и В – глубины стержневой линейкой 3, соединенной с подвижным нониусом.

Винт 4 служит для закрепления нониуса в каком-либо положении. При измерениях штангенциркулем нельзя прилагать к нониусу больших усилий во избежание деформации его ножек.