Эффект Клейна
Эффект
Клейна состоит в прохождении релятивистской
частицы через потенциальный барьер
любой высоты и ширины без ослабления
волны. В графене наблюдается туннельный
эффект с коэффициентом прохождения
,
т. е. барьер не создает сопротивление
носителям тока. Эффект следует из
соотношения неопределенностей Гейзенберга
с учетом рождения-исчезновения частиц
в релятивистской квантовой механике.
Благодаря высокой скорости электрон
находится в области, занятой барьером,
малое время
,
тогда его энергия варьирует на большую
величину
.
За счет этой энергии в области барьера
рождается дырка. Для дырки барьер
перевернут, является ямой, и внутри
барьера дырка движется навстречу
электрону за счет кулоновского
взаимодействия. На входе в барьер
электрон объединяется с дыркой и
аннигилирует. На выходе из барьера
происходит рождение электрона и дырки,
электрон удаляется от барьера, дырка
уходит внутрь барьера. Эффект исследовал
О. Б. Клейн в 1929 г. на основе уравнения
Дирака для частицы со спином 1/2. Он
обнаружил парадокс – при падении
релятивистской частицы массой μ на
потенциальную ступеньку
поток плотности вероятности отраженной
волны превосходит поток падающей волны.
Создание барьера величиной
требует очень сильного поля и эффект
может проявляться лишь в экзотических
случаях, например, при испарении черной
дыры. В графене вблизи уровня Ферми
эффективная масса электрона равна нулю.
В результате эффект Клейна проявляется
в графене при движении носителей тока
через любой барьер.
Рассмотрим
электрон, движущийся в графене вдоль
оси x
с импульсом
,
с энергией
и падающий нормально на прямоугольный
барьер шириной a
и высотой
,
показанный на
рис. 8.4.
Заштрихована
часть зон, заполненных носителями тока.
В областях вне барьера электрон находится
в зоне проводимости и создает электрический
ток, показанный стрелкой. Внутри барьера
носитель тока находится в валентной
зоне, является дыркой, которая движется
с импульсом
,
направленным против оси x.
В точке
электрон аннигилирует с дыркой. При
рождаются дырка и электрон, движущиеся
в противоположные стороны. Учитывая
падающие и отраженные волны на участках
1 и 2, и используя (8.8),
получаем общие решения
,
,
,
где
;
;
;
.
Для нахождения параметров A,
B,
C
и F
используем непрерывность волновых
функций в точках скачка потенциала. Из
условия
находим
,
.
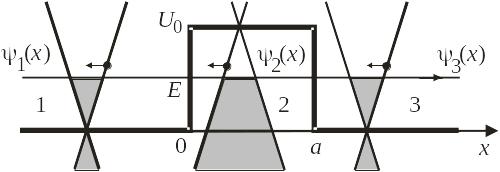
Рис. 8.4. Потенциальный барьер в графене
Условие
дает
,
.
В результате коэффициенты прохождения и отражения
,
(8.23)
не зависят
от характеристик барьера, он прозрачен
и не создает отражения при любой энергии
частицы. Плотность электрического тока
согласно (8.11) на всех участках равна
.
Несмотря
на эффект Клейна, связанные состояния
электрона образуются в потенциальной
яме, возникающей в наноленте графена
шириной
за счет поперечных движений и
перпендикулярного к плоскости графена
магнитного поля.