0. Уравнение Дирака–Вейля

Графен является полупроводником с соприкасающимися в точках Дирака валентной зоной и зоной проводимости. Запрещенная зона имеет нулевую ширину, совпадает с уровнем Ферми, от нее отсчитывается энергия носителей тока. В зоне проводимости носителем тока является электрон, в валентной зоне – дырка. При комнатной и более низкой температуре носители тока находятся вблизи уровня Ферми, имеют нулевую эффективную массу, для них выполняется линейный, т. е. релятивистский закон дисперсии , состояние описывается двухкомпонентной волновой функцией

,

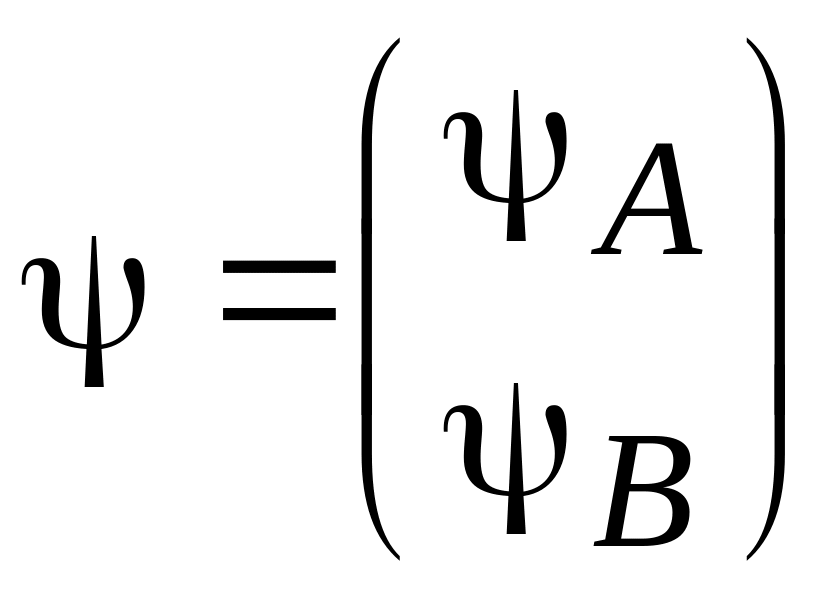где – амплитуда вероятности обнаружения частицы в подрешетке .

Уравнение состояния вблизи точки Дирака K. Для графена, расположенного в плоскости (x,y), гамильтониан носителей тока имеет вид

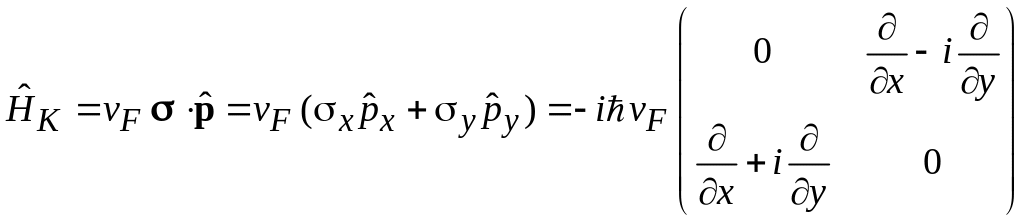, (8.1)

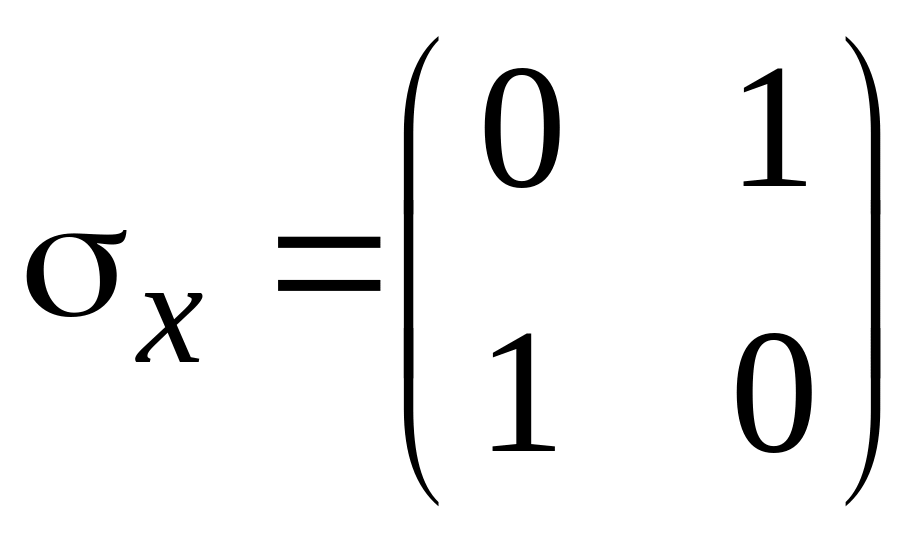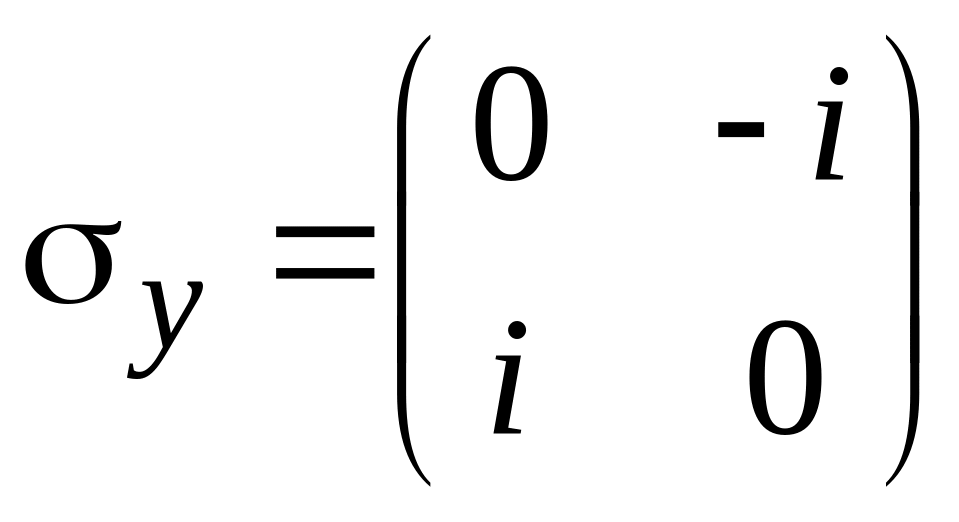
где  скорость на уровне Ферми, ; ; ,  матрицы Паули. Уравнение на собственные функции гамильтониана для частицы с нулевой массой и импульсом является двумерным уравнением ДиракаВейля

, (8.2)

в явной форме

,

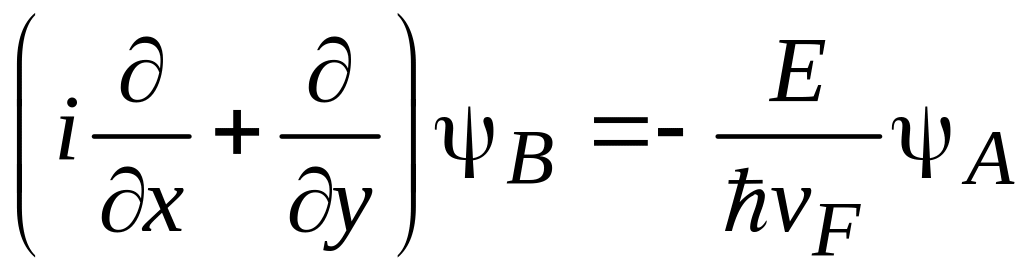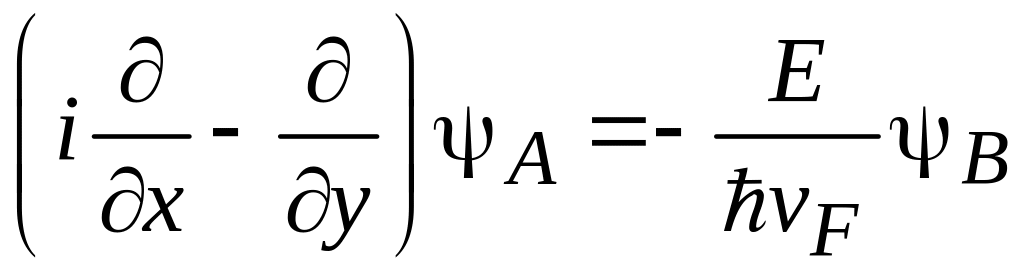. (8.3)

Следовательно, состояние , связанное с подрешеткой A, зависит от ближайшего окружения, т. е. от состояния подрешетки B, и наоборот. Частица во внешнем потенциальном стационарном поле имеет потенциальную энергию . Это приводит к замене в (8.1) , тогда (8.2) получает вид

.

Волновые функции, удовлетворяющие (8.2) и описывающие движение в прямом и обратном направлениях квазиимпульса p, равны

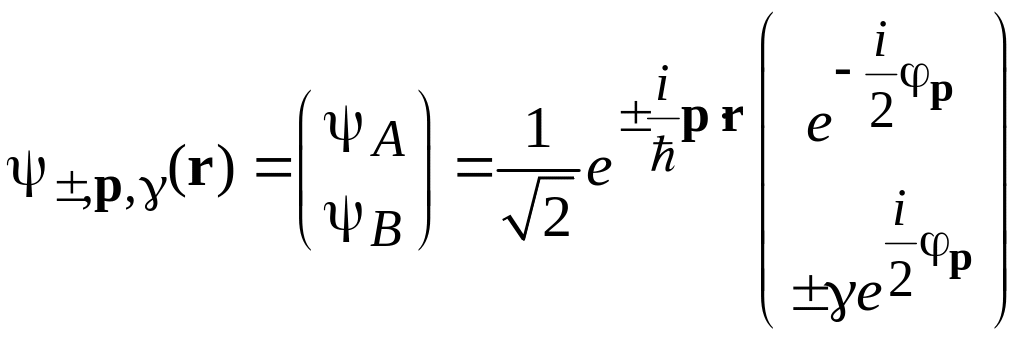, (8.4)

где  угол между квазиимпульсом p и осью x, причем

tg = , ;

– индекс зоны, в которой находится частица; соответствует электрону в зоне проводимости, показанной на рис. 8.2, с энергией ; соответствует дырке в валентной зоне с энергией . Подстановка (8.4) в (8.3) дает дисперсионное соотношение для электронов и дырок

. (8.5)

Состояния электронов и дырок взаимно ортогональны

. (8.6)

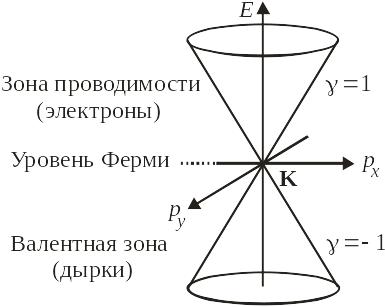
Рис. 8.2. Зоны вблизи точки Дирака K

Операторы скорости для гамильтониана (8.1) находим, используя (2.67а) в виде и , тогда

, , . (8.7)

Волновые функции носителя тока с импульсом, направленным по- или против оси x или y, находим из (8.4)

,

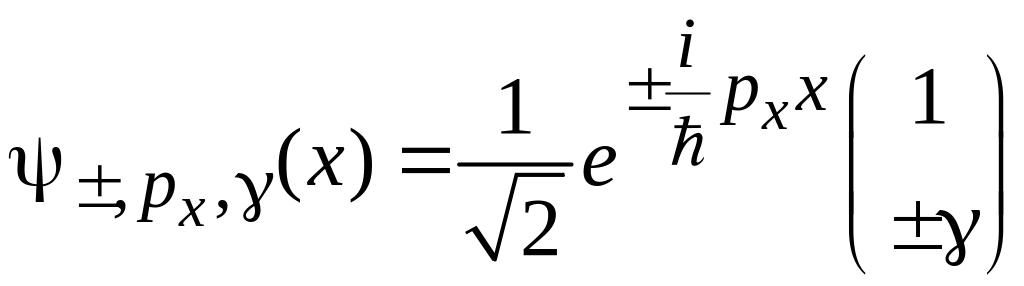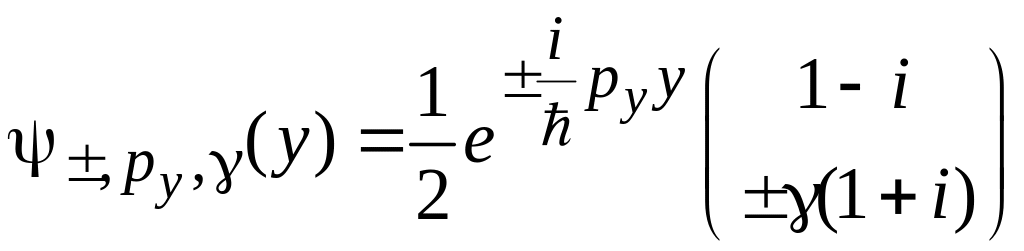. (8.8)

Функции (8.8) являются собственными функциями операторов проекции скорости

,

. (8.9)

Скорость электрона параллельна импульсу, скорость дырки антипараллельна импульсу, модуль скорости равен скорости Ферми.

Плотность электрического тока получаем из (2.71) и (8.7)

. (8.10)

Из (8.9) и (8.10) находим

. (8.11)

Следовательно, электрон и дырка имеют противоположные знаки заряда. Для электрона импульс и плотность электрического тока направлены в противоположные стороны, для дырки – в одну сторону.

Концентрация носителей тока и степень заполнения зон регулируется электрическим напряжением V, прикладываемым между подложкой из кремния и графеном. Величина напряжения ограничена пробоем диэлектрика SiO₂ толщиной d = 300 нм с . Возникающий конденсатор с электроемкостью

обогащает графен электронами или дырками в зависимости от полярности приложенного напряжения. В результате поверхностная концентрация носителей тока пропорциональна напряжению

.

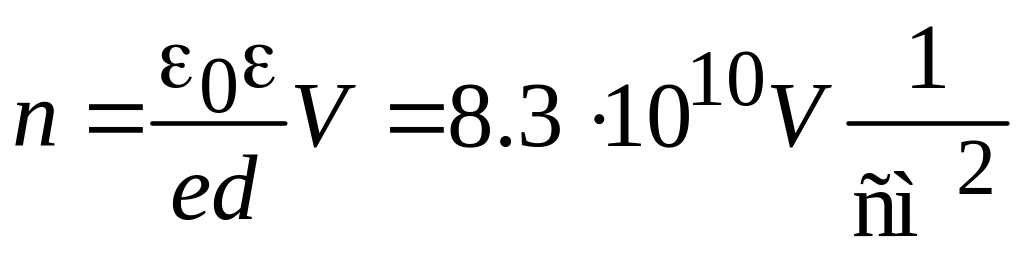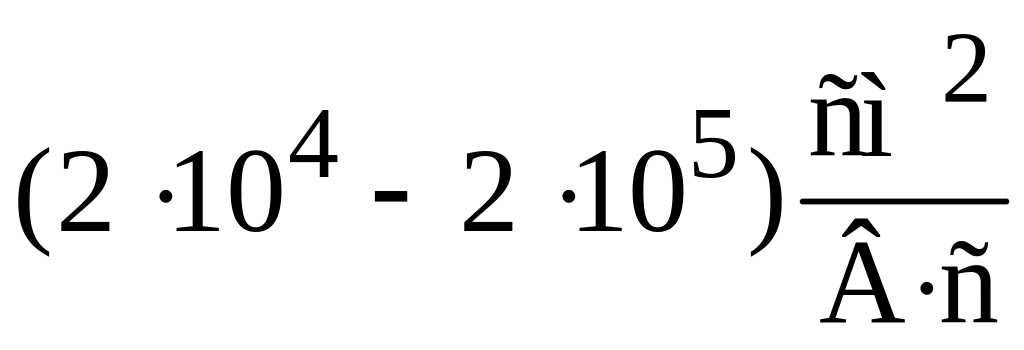Достигнутое значение . Носители тока имеют высокую подвижность , слабо зависящую от температуры, что соответствует баллистическому движению зарядов даже при комнатной температуре.