2.4 Шифраторы, дешифраторы и преобразователи кодов
Схемы, предназначенные для преобразования цифровой информации из десятичной системы счисления в двоичную, обычно называются шифрирующими, а для обратного преобразования – дешифрирующими. Схемы, предназначенные для преобразования различных кодов в двоичной системе, называют преобразователями кода. Все эти схемы относятся к узлам комбинационного типа [4].
Шифраторы. Составление таких схем основано на комбинационной таблице. Здесь показан пример разработки схемы преобразования десятичных цифр 0¸9 в код 8421.
Таблица 2.1 – Комбинационная таблица шифратора
Циф-ра |
Код «1 из 10» |
Код 8421 |
||||||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
D |
C |
B |
A |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Из таблицы (и на рисунке 2.16) видно, что двоичным цифрам 1 в столбике А соответствуют десятичные цифры 1, 3, 5, 7 и 9, т. е. можно написать: А = 1 + 3 + 5 + 7 + + 9. Это алгебраическое выражение логического сложения. Точно так же справедливо, что: В = 2 + + 3 + 6 + 7; С = 4 + 5 + 6 + 7; D = 8 + 9 . На рисунке 2.16 представлен пример реализации схемы на элементах ИЛИ-НЕ. В состоянии покоя на всех входах низкий уровень. Подобным образом можно составить схемы преобразования десятичных цифр в любой код.
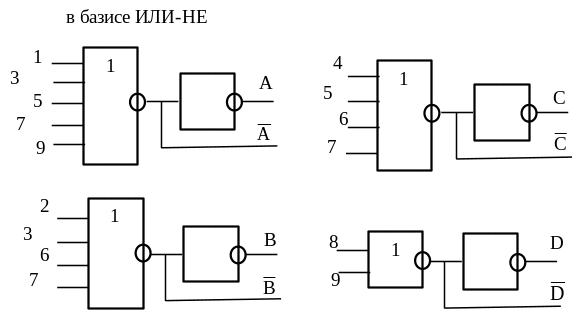
Рисунок 2.16 – Шифратор цифр 0¸9 в код 8421
Дешифраторы. При разработке различного рода цифровых управляющих устройств часто необходимо решать задачу, когда управляющее воздействие определяется значениями входных сигналов только в данный момент времени и не зависит от их значений в предыдущие моменты времени. Иными словами, выходной сигнал, характеризующий управляющее воздействие, здесь зависит только от наличия соответствующей комбинации сигналов на входах устройства. Примером таких комбинационных схем являются дешифраторы.
Дешифратором называют комбинационную логическую схему, в которой каждой из комбинаций сигналов на входах соответствует сигнал только на одном из его выходов. Они находят применение в управляющих системах для выдачи управляющих воздействий в те или иные цепи в зависимости от комбинации сигналов на входах.
Значения сигналов
а, b,
с, d
на выходах счетчика и требуемые при
этом показания дешифратора могут быть
использованы для определения элементов
схемы дешифратора. Так, при нулевом
показании счетчика сигнал «1» присутствует
на инверсных выходах его триггеров (см.
таблицу 2.2), в связи с чем реализуемая
каналом х0
функция будет: x0
=
.
Таблица 2.2 – Состояния дешифратора
Число входных импульсов |
Триггеры счётчика |
Выходы дешифратора |
||||||||||||
Тр4 (d) |
Тр3 (с) |
Тр2 (b) |
Тр1 (a) |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
6 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
9 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Аналогично для
канала x1
имеем: х1
= a
;
а для канала
х9:
x9 =
a
.
Логические функции могут быть реализованы
с помощью четырехвходовых логических
элементов И.
Однако без
предварительной минимизации составленные
непосредственно из таблицы дешифрируемые
функции нецелесообразно использовать
для схемной реализации. Это привело бы
к заведомому усложнению схемы дешифратора.
Табличное выражение дешифрируемой
функции для цифры 9 (канала
x9)
имеет вид x
= a
d.
Вместе с тем, только для этого канала
характерна комбинация выходных сигналов
триггеров счетчика, при которой а
= d
= 1. В связи
с этим для выделения сигнала (логической
«1») по каналу цифры 9 можно воспользоваться
функцией x9 = ad.
Иными словами, канал x9
можно реализовать не на четырёхвходовом,
а на двухвходовом логическом элементе
И.
Минимизацию функций дешифратора удобно проводить по карте Карно, которая составляется в данном случае для четырех переменных. Данные таблицы 2.2 используют для определения функций каналов дешифратора x0, х1, x2, ..., x9 и их изображения на карте Карно (рисунок 2.17).
Рисунок 2.17 – Карта Карно дешифратора
Минимизирующие
контуры составляют индивидуально для
каждой функции и проводят с использованием
пустых клеток карты. При этом минимизирующий
контур должен охватывать максимальное
число соседних с рассматриваемой
функцией пустых клеток. Из карты Карно
находим: х0=
,
x1=
a
,
x2
=
b
,
x3
= ab
,
x4 =
c,
х5
= a
c,
x6
=
bc,
x7
= abc,
х8
=
d,
x9
= ad.
Найденные функции используют для
построения схемы дешифратора (рисунок
2.18).
Рисунок 2.18 – Дешифратор двоично-десятичного кода в десятичный
Электронная промышленность выпускает дешифраторы в виде интегральных схем, например, в серии 1533 интегральные схемы КР1533ИД3, КР1533ИД6. ИХ условное графическое обозначение приведено на рисунке 2.19.
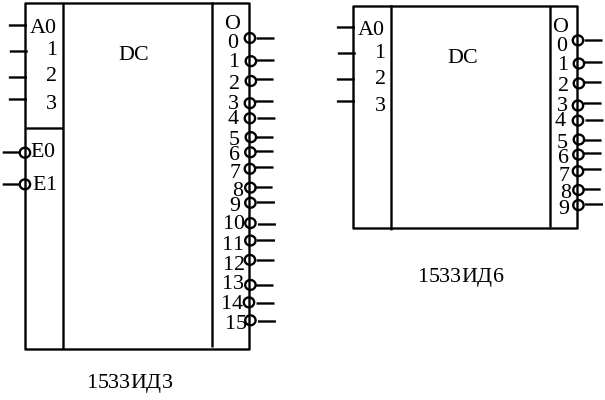
Рисунок 2.19 – Интегральные схемы дешифраторов серии 1533
Преобразователи кодов. Преобразователем кодов называется логическое устройство, предназначенное для изменения кода информации, передаваемой и обрабатываемой цифровыми устройствами. Существующее множество кодов предназначено для обеспечения удобства перевода чисел из десятичной системы в двоичную, простоты выполнения арифметических операций и контроля результатов вычислений. Выбор кода влияет также на аппаратные затраты реализуемых схем цифровых устройств и на надежность выполнения ими заданных алгоритмов.
Рассмотрим синтез комбинационных преобразователей кодов на примерах преобразования двоично-десятичного кода 8421 в широко применяемый в цифровых устройствах двоично-десятичный код 2421. Алгоритм преобразования двоично-десятичного кода 8421 в код 2421 может быть представлен таблицей истинности (таблица 2.3).
Таблица 2.3 – Таблица истинности преобразователя кода 8421 в код 2421
Десяти- чное число |
Код |
|||||||
8421 |
2421 |
|||||||
x4 |
x3 |
x2 |
x1 |
F4 |
F3 |
F2 |
F1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
6 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
9 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Выполним синтез схемы преобразователя в код 2421 на основе карт Карно (рисунок 2.20). С целью минимизации доопределим значения переключательных функций на некоторых избыточных наборах входных переменных, которые показаны на картах знаком X.
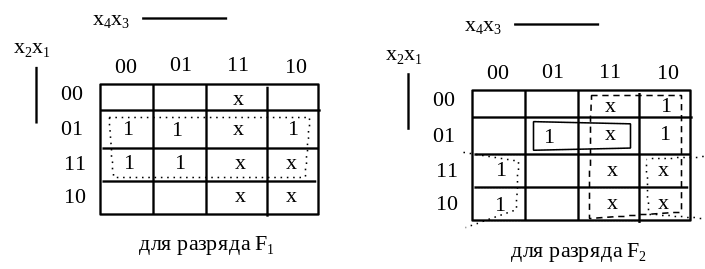
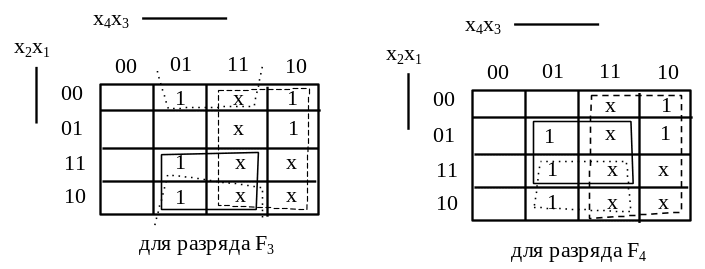
Рисунок 2.20 – Карты Карно выходных функций преобразователя
кода 8421 в код 2421
В соответствии с петлями покрытий минимизированные выражения для переключательных функций выходов, приведенные к виду, удобному для реализации на логических элементах И-НЕ, могут быть записаны в виде уравнений:
F1
= x1,
, (2.8, 2.9)
при: 5 ® 0101; 6 ® 0110; 7 ® 0111.
(2.10)
при 5 ® 0101; 6 ® 0110; 7 ® 0111.
(2.11)
при 5 ® 0101; 6 ® 0110; 7 ® 0111.
Схема, построенная на основании этих структурных формул, представлена на рисунке 2.21.
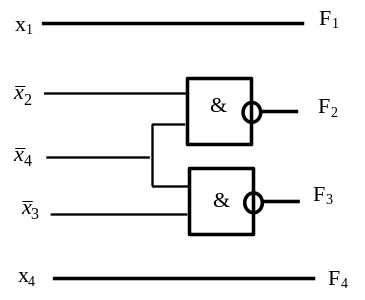
Рисунок 2.21 – Преобразователь кода 8421 в код 2421
(Пояснение преобразований для преобразователя кодов)
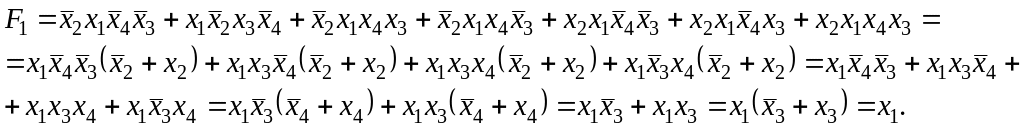
и
так далее.