Задача 3

Найти частоту колебаний поплавка на воде, если он плавает в воде в вертикальном положении, его масса т, площадь поперечного сечения S. Каким должен быть поплавок, имеющий малую амплитуду колебаний при наличии волн на поверхности воды?

Решение

В положении равновесия сила тяжести уравновешена силой Архимеда. Но если поплавок сместить из положения равновесия, то векторная сумма F силы Архимеда и силы тяжести будет отлична от нуля и направлена навстречу перемещению поплавка, т.е. при его погружении она направлена вверх, при подъёме из воды – вниз. Поэтому эту сумму сил можно записать в виде:

F_x = ‒ gSx.

Здесь х – смещение поплавка из положения равновесия (при погружении x > 0), а  – плотность воды.

Рис. 1

Соответственно, уравнение движения поплавка массы m имеет вид:

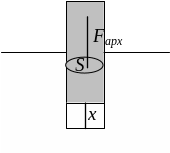
та_x = – gSx.

Записав ускорение как вторую производную по времени от перемещения поплавка, получим уравнение:

.

Поделив обе части уравнения на массу поплавка, и перенеся все члены уравнения в одну сторону, получим уравнение гармонических колебаний:

.

Рис. 2

Коэффициент перед х даёт квадрат частоты колебаний:

.

Полученный ответ показывает, что лучший поплавок для рыбной ловли, который остаётся практически неподвижным при наличии волн на воде, должен иметь малое поперечное сечение и большую массу (Рис. 2). В этом случае частота его колебаний будет малой по сравнению с частотой колебаний волн на воде. Это приводит к малой амплитуде колебаний поплавка под действием волн. Обоснуйте сами эти выводы, а для подсказки обратитесь к п.10 введения к данному разделу.

Задача 4

Найти период колебаний маятника, находящегося на тележке, которая движется с ускорением а.

Решение

Рис. 1

В системе отсчёта, которая движется вместе с тележкой, на маятник помимо силы натяжения нити и силы тяжести, действует ещё и сила инерции ‑ ma. Сила инерции пропорциональна массе тела, однородна и поэтому ничем не отличается от силы тяжести. И в этом смысле можно рассматривать эту силу как добавочную силу тяжести. Иными словами, в системе отсчёта, связанной с тележкой на маятник действует сила тяжести:

,

величина соответствующего ускорения "свободного падения" равна:

.

Тем самым частота колебаний маятника:

.

Задача 5

Тело массы т движется по горизонтальному гладкому стержню, к концам которого оно прикреплено двумя невесомыми одинаковыми пружинами жёсткости k. Стержень вращается вокруг вертикальной оси с угловой скоростью . Найти частоту  колебаний тела относительно его равновесного положения.

Решение

Рис. 1

Перейдём в систему отсчёта связанную со стержнем. Здесь на тело действуют упругая и центробежная силы:

.

Как видим, сила пропорциональна отклонению тела от положения равновесия. Следовательно, тело совершает гармонические колебания с частотой :

Нетрудно понять, что колебания будут иметь место лишь при малой скорости вращения, пока подкоренное выражение положительно:

Подумайте сами, что произойдёт при нарушении этого неравенства.

Задача 6

Найти частоту малых колебаний относительно равновесного положения тела из задачи 6 раздела 8.