Задача 7

Суточное вращение Земли вокруг своей оси приводит к тому, что Земля оказывается слегка сплющенной с полюсов, т.е. расстояние между её полюсами несколько меньше, чем диаметр Земли в экваториальной плоскости. Найти разность экваториального и полярного радиусов Земли.

Решение

Рис. 1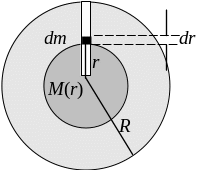

Вопросом о форме Земли интересовались многие учёные, в том числе и Ньютон. Рассмотрим решение, предложенное Ньютоном. Будем считать, что форма Земли очень мало отличается от шарообразной (потом мы убедимся в справедливости этого предположения). Мысленно просверлим от поверхности Земли до её центра два канала. Один от полюса к центру, а второй от экватора к центру. Заполним эти каналы доверху жидкостью, например, водой. Тогда давление в обоих каналах в центре Земли будет одинаковым. Вычисление давления без учёта вращения Земли было проделано в задаче 8 раздела 2 (Законы Ньютона). Этот же результат годится для канала, заполненного водой и идущего от полюса к центру Земли:

(1).

Здесь R_полюс – полярный радиус Земли, ' – плотность воды

Для канала, идущего к центру Земли от экватора, необходимо учесть ещё центробежную силу, которая несколько ослабляет действие силы тяжести. Воспользуемся полученными в этой задаче уравнениями, добавив в них центробежную силу:

(2).

Сила тяготения, согласно упомянутой задаче, равна:

,

а центробежная сила:

F_цб = dm²r.

Здесь  – плотность Земли, dm ='dr.

Тем самым, уравнение (2) приобретает вид:

.

Интегрируя по dr от нуля до R_{экватор}, получим:

(3).

Приравнивая (1) и (3), получим:

Экваториальный радиус в правой части заменим средним радиусом Земли и тогда окончательно получим:

Наш результат показывает, что исходное предположение о слабом искажении формы Земли под действием центробежной силы оказалось верным. Действительно, по данным, приведенным в справочнике К.У. Аллена "Астрофизические величины", экваториальный радиус Земли равен 6378,164±0,003 км, а полярный радиус составляет 6356,779 км. Их разность 21,385 км прекрасно согласуется с нашим результатом.

Полученный результат даёт лишь ответ на вопрос о том, каково различие полярного и экваториального радиусов Земли. Для ответа на вопрос о форме Земли пришлось бы составлять и решать значительно более сложные уравнения.

9. Колебания

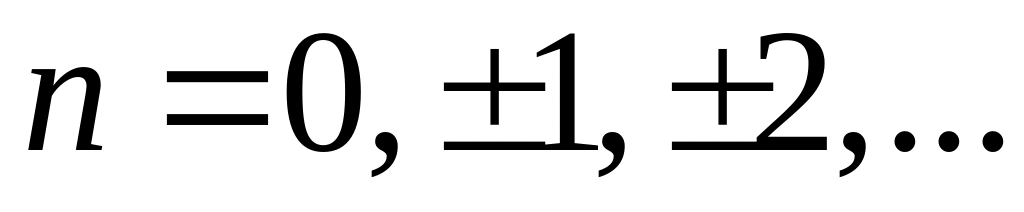
1. Колебательное движение отличает большая или меньшая степень повторяемости. Предельная, полная повторяемость – это периодический процесс, зависимости характеристик которого от времени описываются периодическими функциями вида , где период.

2. Особую роль в физике играет периодическое движение, в котором координаты тела изменяются со временем по закону:

x(t) = A cos (t + ) (1),

где А, ,  – некоторые константы (причем А и  положительные). Такое движение называется гармоническими колебаниями. Причина такой «особости» гармонических колебаний в том, что всякий периодический процесс можно представить как сумму (возможно, бесконечную) гармонических колебаний.

3. Величина А называется амплитудой гармонических колебаний, она определяет размах колебаний:

|x(t)|  A,

 – частота колебаний, связана с их периодом T соотношением:

(2).

Аргумент косинуса t +  называется фазой колебания,  – начальная фаза (в момент t = 0).

4. Скорость и ускорение тела , совершающего гармонические колебания, также изменяются по гармоническому закону:

(3).

5. Последнее из уравнений показывает, что сила F_х = ma, действующая на тело, совершающее гармонические колебания, зависит от координат тела следующим образом:

F_х = – m²x,

или, обозначая k = m²:

F_х = – k x (4).

Силы такого типа принято называть квазиупругими (т.е. похожими на упругие). Результат (4) можно трактовать иначе: если F_x = – kх, то собственная частота колебаний тела связана с массой тела m и коэффициентом k следующим образом:

.

6. Зависимость потенциальной энергии тела U(x), совершающего гармонические колебания, от координаты тела х получается из (4):

7. Второе из соотношений (3) можно записать в виде:

(5).

Это уравнение называют уравнением гармонических колебаний, решением которого, как видим, является (1). Отметим, что частота колебаний определяется коэффициентом при х, а что касается амплитуды и начальной фазы колебаний, то они определяются начальным положением тела и его начальной скоростью.

8. Так как сила, действующая на тело, совершающее гармонические колебания, консервативна, то при гармонических колебаниях справедлив закон сохранения энергии:

Если продифференцировать это уравнение по времени, то вновь придём к уравнению гармонических колебаний. Этот способ вывода уравнения колебаний часто используется в задачах.

Поскольку энергия сохраняется, то найдя её в момент наибольшего отклонения тела от положения равновесия, когда х = А, получим:

Как видим, энергия пропорциональна квадрату амплитуды колебаний.

9. При наличии силы трения, пропорциональной скорости  тела:

F_тр = ,

уравнение колебаний имеет вид:

(6),

где 2 = /m – величина, характеризующая силу трения и называемая коэффициентом затухания. Решение уравнения (6) имеет вид:

(7).

Как видим, такое движение тела можно приближенно рассматривать как гармоническое колебание с экспоненциально уменьшающейся амплитудой. В точном смысле такой процесс не является ни гармоническим колебанием, ни периодическим процессом. Такие колебания называют затухающими. Частота затухающих колебаний  оказывается несколько меньше, чем в отсутствие трения, что вполне понятно, поскольку трение замедляет движение тела.

10. Если кроме силы (3) и силы трения на тело действует еще и внешняя гармоническая сила F(t) = F₀ cost, то уравнение движения тела имеет вид:

.

Движение, которое будет совершать тело в данном случае, представляет собой сумму (суперпозицию) затухающего и вынужденного, т.е. вызванного внешней силой, колебаний. По истечении достаточно большого времени после начала колебаний (t >> 1) затухающие колебания прекратятся, и тело будет совершать гармонические колебания с частотой внешней силы  и амплитудой, зависящей от величины внешней силы и её частоты:

.

Отметим, что энергия установившегося вынужденного колебания постоянна, хотя колеблющееся тело непрерывно поглощает энергию (от источника внешней силы), которая превращается в тепло благодаря наличию трения.

Если изменять частоту внешней силы , то будет изменяться и амплитуда вынужденных колебаний, причем она имеет максимум при частоте внешней силы _рез:

.

Явление возрастания амплитуды вынужденных колебаний при частоте внешней силы, совпадающей с резонансной частотой _рез, называется резонансом.

11. Материальная точка, подвешенная на невесомой и нерастяжимой нити, называется математическим маятником. Частота его малых колебаний определяется лишь длиной маятника и ускорением свободного падения:

,

где l – длина нити.

12. Твердое тело, совершающее колебания в вертикальной плоскости вокруг неподвижной точки или горизонтальной оси под действием силы тяжести, называется физическим маятником. Частота его малых колебаний:

,

где m – масса тела, d – расстояние от оси вращения до центра масс тела, I – момент инерции тела относительно оси вращения.

Период колебаний физического маятника совпадает с периодом колебаний математического, если длина последнего l_привед определяется следующим равенством:

.

Ее называют приведенной длиной физического маятника.

Задача 1

Частица массой т совершает гармонические колебания с частотой . В начальный момент частица находилась в точке с координатой х₀ и двигалась со скоростью v₀. Найти амплитуду и начальную фазу колебаний.

Решение

Согласно условию задачи:

x(t) = Acos(t +).

Начальные условия дают:

x(0) = A cos ,

v(0) = – Asin .

Разделив второе уравнение на первое, получим:

.

Разделив второе уравнение на , и возведя оба уравнения в квадрат, а затем, сложив их, получим:

.

Задача 2

Стержень массы m и длины l подвешен за два конца нитями в точке О (рис. 1а). Расстояние от точки подвеса до стержня равно h. Найти частоту колебаний этого маятника. Как изменится частота, если нити будут параллельны друг другу (рис. 1б)?

Решение

а) б)

Рис. 1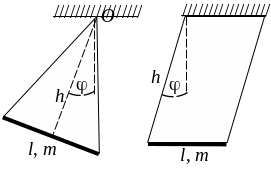

В случае а) мы имеем дело с физическим маятником, частота колебаний которого равна:

Момент инерции вычисляем по теореме Штейнера:

где ml²/12 - момент инерции стержня относительно оси, проходящей через его центр масс. Окончательно получаем:

(1).

В случае б) стержень совершает поступательное движение, т.е. никакого вращения нет. Можно поэтому предположить, что стержень колеблется как математический маятник длины h, т.е. его частота:

(2).

Результат (2) является не более чем догадкой, но его можно получить и строгим путём, если учесть, что колебания незатухающие, а потому полная энергия тела остаётся постоянной. Энергия, в свою очередь, равна сумме кинетической энергии поступательно движущегося тела и потенциальной энергии. Если положение стержня характеризовать с помощью  – угла отклонения нитей от вертикали, то его скорость:

.

Потенциальную энергию будем отсчитывать от уровня подвеса нитей, тогда

U = – mghcos.

Таким образом, энергия маятника:

.

Так как Е = const, то dE/dt = 0, откуда получаем:

(3).

Если угол отклонения мал (||<<1), то sin  = , и из (3) получаем уравнение гармонических колебаний:

.

Как видно из полученного уравнения, частота колебаний действительно совпадает с частотой колебаний математического маятника

.