Задача 13

Шар массы m и радиуса R раскрутили вокруг его горизонтальной оси до угловой скорости ₀ и опустили на горизонтальную плоскость. С какой скоростью покатится шар, после того, как проскальзывание прекратится?

Решение

Задача допускает различные способы решения. Рассмотрим два из них.

Способ 1

В процессе движения на шар действуют три силы (рис.1): тяжести – тg, нормальная компонента силы реакции плоскости – N и сила трения – F_тр. Нетрудно понять, что пока шар катится с проскальзыванием, сила трения направлена вперед (поясните это утверждение самостоятельно).

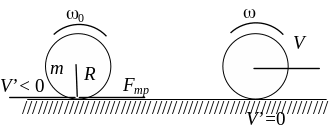
Рис. 1

Составим систему уравнений, описывающих движение шара:

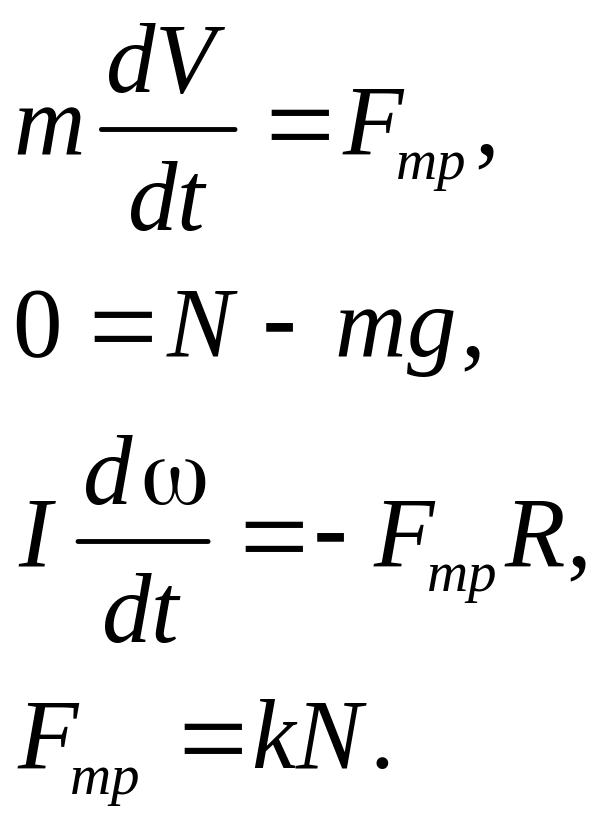
Первые два уравнения – проекции уравнения движения центра масс шара на горизонтальное и вертикальное направления. Третье – уравнение моментов, причём моменты вычисляются относительно оси вращения шара. Знак минус в правой части этого уравнения отражает то обстоятельство, что сила трения замедляет вращение шара. Но так как сила трения одновременно и ускоряет центр масс шара, то в первом уравнении она стоит со знаком плюс. Последнее уравнение справедливо лишь до тех пор, пока шар движется с проскальзыванием, т.е. пока F_тр – сила трения скольжения. Исключая из этих уравнений силу N, получим F_тр = kmg, и с учетом этого получаем уравнения для V и :

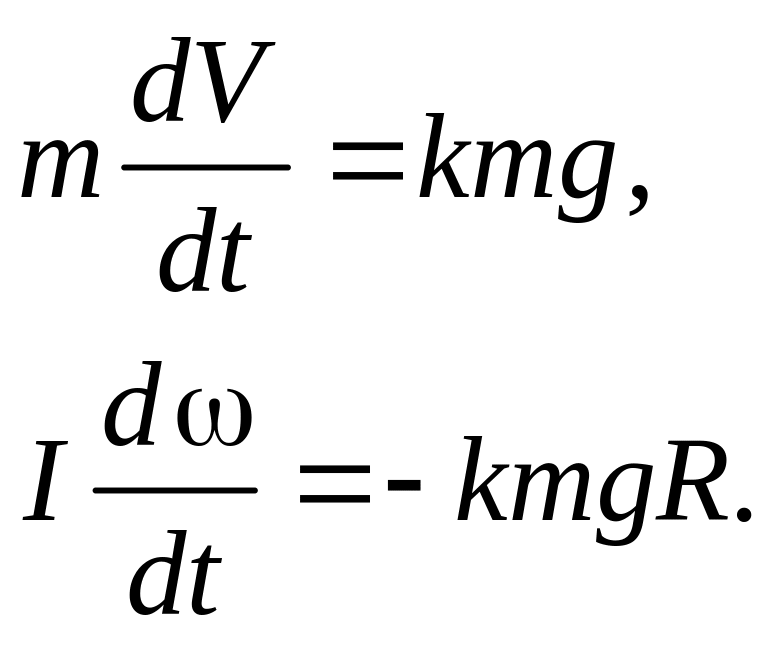
Откуда, после интегрирования по времени при заданных начальных условиях получаем:

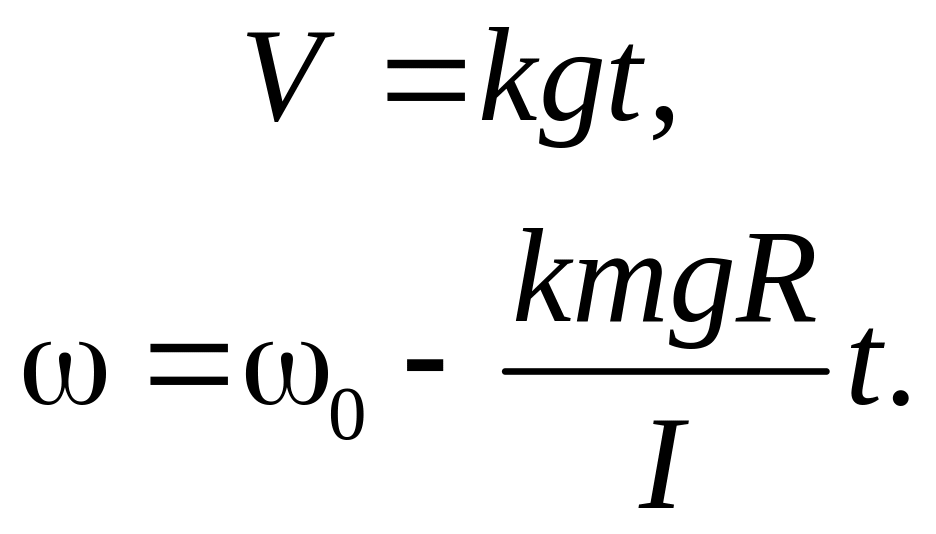
Зная V и , найдем V' - скорость точки соприкосновения шара с плоскостью:

Как видим, V'< 0 при достаточно малых t, что соответствует движению шара с проскальзыванием. Проскальзывание прекращается в тот момент, когда V'=0, откуда и находим соответствующее значение t:

а затем скорость центра инерции шара и его угловую скорость в этот момент:

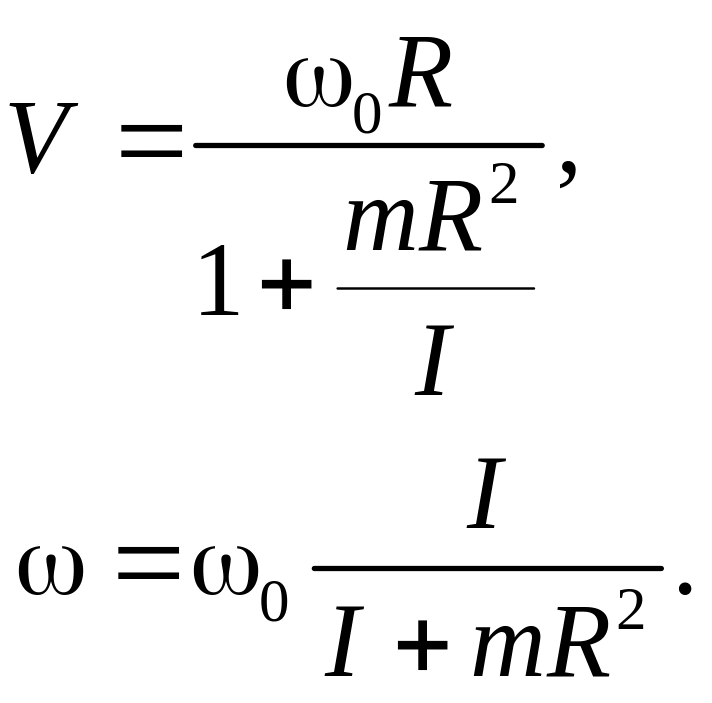
Для однородного шара:

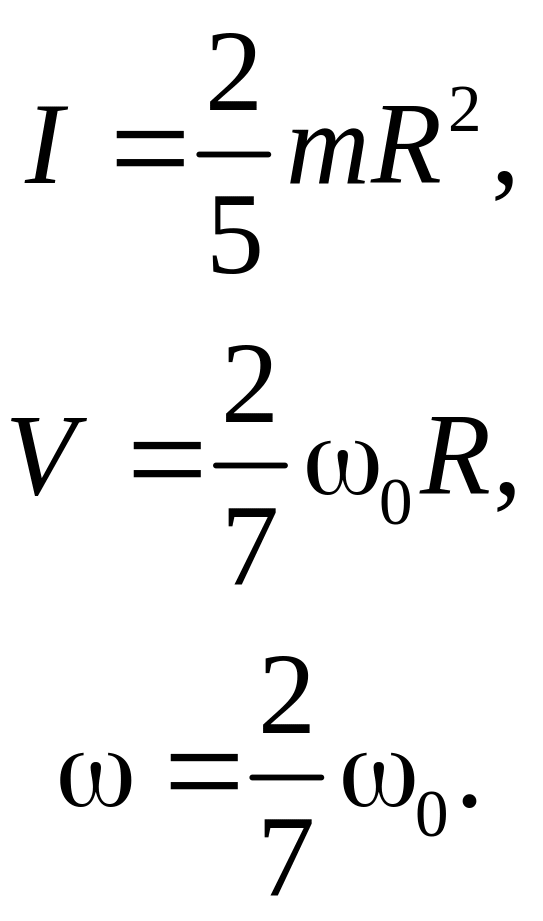
Интересно, что конечные скорости совершенно не зависят от величины коэффициента трения.

Способ 2

Этот метод основан на применении теоремы Кёнига для момента импульса системы точек:

L = [R_ци,P] + L₀,

где L₀ – момент импульса системы точек относительно ее центра масс, R_ци – радиус-вектор центра масс системы, Р – импульс системы. В нашем случае система точек – это шар, который вращается (в системе отсчета, в которой центр шара покоится) вокруг своего диаметра, т.е. вокруг главной оси инерции, поэтому L₀ = I, где I – момент инерции шара относительно его диаметра.

Рассмотрим момент импульса шара относительно точки касания шара с плоскостью в начальный момент времени. Нетрудно видеть, что сумма моментов сил, действующих на шар, относительно этой точки равна нулю. Действительно, сила тяжести и сила реакции опоры направлены вдоль одной прямой и их сумма равна нулю, поэтому и сумма моментов этих сил равна нулю.

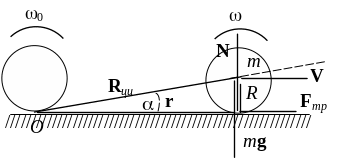
Рис. 2

Сила трения коллинеарна радиус-вектору r её точки приложения, поэтому её момент также равен нулю. Таким образом, в силу уравнения моментов, момент импульса шара относительно точки О остаётся постоянным. Но в начальный момент времени импульс шара равен нулю, поэтому величина момента была равна L = I₀. В последующие моменты времени его величина находится с помощью теоремы Кёнига для момента импульса системы точек:

L = [R_ци,P] + L₀,

L = R_циmVsin + I = RmV + I.

Итак:

I₀= RmV + I.

После того, как скольжение прекратится, скорость точки касания шара с плоскостью станет равной нулю:

V – R = 0,

откуда и: