5.Предварительные замечания.

Обычно, начиная изучать механику, многие студенты исходят из мне­ния, что это очень простая наука, решать задачи по механике можно, ис­пользуя лишь свой житейский опыт, а основные понятия, о которых что–то твердит преподаватель на лекциях, лишь малосущественное дополнение к этому житейскому опыту. Естественно, "суровая действительность" теку­щих занятий, контрольных, зачетов и экзаменов заставляет многих отка­заться от этого мнения и впасть в другую крайность, которая тоже дале­ка от истины. Поэтому следует сразу же принять к сведению следующее: наши житейские представления зачастую имеют весьма мало общего с научными представлениями и не могут служить надежной основой для изучения точ­ных наук. Поэтому начинать изучение механики следует с твердого усвое­ния основных ее понятий, если угодно, даже заучивания их. Да, заучивания! Не надо этого стесняться. Классической (Ньютоновской) механике, более трёхсот лет. За это немалое время формулировки определений, законов, принципов и т.п. полностью отработаны, и трудно себе представить, что студенту, только начинающему её серьёзное изучение, придет в голову что-то полезное новое. Начните с того, что выучите их, когда придет достаточно глубокое их понимание, придёт автоматически и способность грамотно изложить их своими словами. Естественно, что такая способность только приветствуется.

1. Кинематика материальной точки

Кинематика описывает движение тел, устанавливает характеристики движения, но причины, вызвавшие движение, ею не рассматриваются. Наиболее простой объект для описания – материальная точка, т.е. тело, размерами которого в условиях данной задачи можно пренебречь. Наряду с термином "материальная точка" будем пользоваться также термином "частица".

1. Положение частицы в пространстве задается либо ее координатами, либо радиус-вектором, проекции которого на координатные оси совпадают с координатами частицы (Рис. 1):

r_x = х, r_у= y, r_z = z.

Сам же радиус-вектор r запишется тогда в виде:

r = e_x  x + e_y  y+ e_z  z,

Рис.1

где e_x, e_y, e_z – направляющие единичные векторы (орты) координатных осей.

2. Для такого описания нужно каким-то образом задать систему координат, связанную с некоторым телом, т.е. систему отсчёта. Обычно задают декартову систему координат, хотя нередко используют и другие координатные системы. Выбор системы отсчёта ничем не ограничен, можно выбирать любую удобную систему отсчёта.

3. Если точка движется, то ее координаты x, y, z или, что то же самое, ее радиус–вектор r, будут изменяться с течением времени. Если известна зависимость координат от времени t, т.е. заданы х, у, z (или r) как функции t:

x=x(t), y=y(t), z=z(t),

r=r(t),

то говорят, что задан закон движения.

4. Если в моменты времени t₁ и t₂ положение точки характеризовалось радиус–векторами r(t₁) и r(t₂), то вектор

r = r(t₁) – r(t₂)

называется перемещением точки за время t = t₁ – t₂, вектор

v_cp=r /t

называется вектором средней скорости за время t.

5. Скорость точки:

,

а ее проекции на оси координат:

6. Вектор скорости v направлен по касательной к траектории точки. Это иллюстрируется рис.2, где изображена траектория точки и радиус-векторы r(t₁) и r(t₂) в два момента времени t₁ и t₂. Там же изображены векторы скорости v(t₁) и v(t₂) в эти же моменты времени.

Рис. 2

7. Ускорение точки a=dv/dt, его проекции на координатные оси:

8. Вектор ускорения а можно представить в виде суммы двух векторов:

а = a_n + a_

Здесь a_ и а_n – векторы тангенциального и нормального ускорений. Эти векторы определяются следующим образом:

=|v|

В свою очередь, векторы  и n - это векторы единичной длины. Направление вектора  совпадает с направлением вектора скорости v:

v = ,

Рис. 3

а вектор n перпендикулярен вектору скорости v и направлен в сторону, куда траектория вогнута (см. рис. 3). Можно утверждать, что каждый бесконечно малый участок кривой можно рассматривать как дугу окружности. Радиус этой окружности R называется радиусом кривизны кривой в данной точке. Разумеется, в разных точках кривой эти радиусы могут быть различны. Физический смысл векторов a_ и а_п следующий. Вектор a_ характеризует быстроту изменения модуля скорости, вектор же а_п характеризует быстроту изменения направления скорости. Отметим еще, что a_ направлен в сторону движения, если d/dt>0 , т.е.когда величина скорости растет (ускоренное движение), и, соответственно, он направлен в обратную сторону, когда d/dt < 0, т.е. величина скорости убывает (замедленное движение).

9. Как было отмечено выше, выбор системы отсчёта ничем не ограничен, можно выбирать любые системы отсчёта. Связь между значениями скоростей v и v' одной и той же материальной точки в двух различных си­стемах отсчета¹ К и К' даётся правилом сложения скоростей:

v' = v + V,

где V – скорость системы К относи­тельно К'.

Хотя правило сложения скоростей представ­ляется совершенно очевидным, однако, нужно иметь в виду, что оно основано на предпо­ложении об абсолютном течении времени. Именно, мы счи­таем, что интервал времени, за который частица смещается на величину ds в системе К, равен интервалу времени, за который частица смещается на соответствующую величину ds' в системе К'. Это предположение в действительности оказывается, стро­го говоря, неправильным, но следствия, вытекающие из неабсолютности времени, начинают проявляться только при очень больших скоростях, сравнимых со скоростью света. В частности, при таких скоростях уже не выполняет­ся правило сложения скоростей. Мы в дальнейшем будем рассматривать лишь достаточно малые скорости, когда предположение об абсолютности времени хорошо оправ­дывается.

Задача 1.

Материальная точка движется вдоль оси ОХ по закону

где b – некоторая константа, а х – координата точки. Найти: зависимость от времени скорости _x = _x(t), координату точки х как функцию времени x = x(t), ускорение точки а_х. Учесть, что в момент времени частица находилось в точке с координатой .

Решение.

Так как по определению _x = dx/dt, то, учитывая условие задачи, получим уравнение:

Интегрируя, получим:

Константу С выбираем так, чтобы, согласно начальному условию, х = 0 при t = 0, получаем С=0, откуда:

Найдем скорость v(t):

.

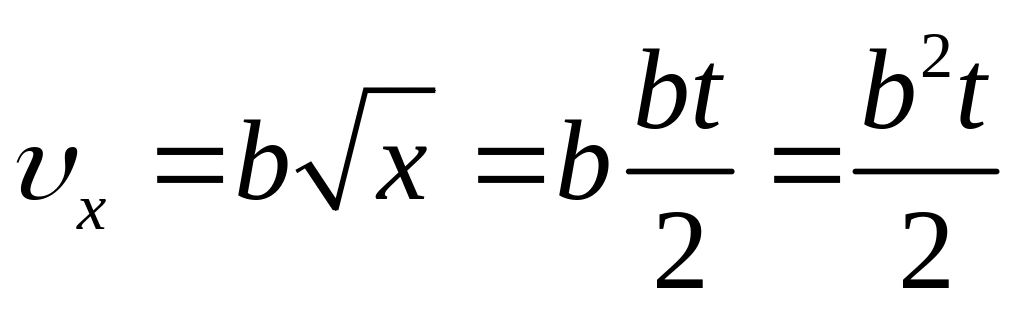Ускорение:

Таким образом:

Как видим, движение является равноускоренным с нулевой начальной скоростью.

Задача 2.

Материальная точка движется вдоль прямой по закону:

x(t) = bt(c – t/2),

где b и с некоторые положительные константы, t – время движения, x(t) – координата тела в момент t. Найти: скорость тела, как функцию времени _x = _x(t), среднюю скорость тела за первые t секунд движения, ускорение и путь, пройденный телом за первые t секунд.

Решение.

Согласно определениям скорости, ускорения и средней скорости, находим скорость _x = dx/dt, дифференцируя x(t) по времени t:

_x (t) = b(c – t).

Повторное дифференцирование дает ускорение:

a_x = d_x/dt = – b

Полученный результат показывает, что тело движется с постоянным ускорением, знак минус означает, что направление ускорения противоположно направлению оси ОХ. При , когда движение равнозамедленное, а при , когда , движение равноускоренное. Подробный анализ дан ниже.

Средняя скорость:

_cp(t) = [x(t) – x(0)] /t = b(c – t/2).

Рис. 1

Найдем теперь путь S, пройденный телом за первые t секунд его движения. Здесь следует учесть, что путь S(t) и перемещение x(t) – это вещи разные. Нагляднее всего это видно в случае, когда траектория тела является некоторой кривой (см. рис. 1). На рис.1 вектор r(t) – перемещение за время t, а длина кривой АВ – путь S(t), пройденный за это же время.

Для нахождения S(t) разобьем кривую АВ на много малых частей, таких, что каждую из них можно считать отрезком прямой, тогда для каждой из этих частей dS = |v| dt (см. Рис. 1). Интегрируя это равенство, получим:

.

В нашем случае _x (t) = b(c – t), поэтому для модуля скорости находим:

|_x (t) | = b(c – t), если t < c,

|_x (t) | = b(t – с), если t > c.

Тогда при t < с получаем:

Если же t > c, то:

Итак:

Посмотрим, что же мы получили. Как видим, путь и перемещение совпадают, пока t < c. Пусть t < c. Так как _х(t) = b(c – t), то при t < с тело движется вправо ((t) > 0). При t = с тело останавливается (_х(t) = 0) в точке с координатой х = bс²/2.

Для t > c картина сложнее. При t > с скорость отрицательна, т.е. направление движения изменяется на обратное и тело движется влево. При t = 2с оно вновь окажется в начале координат, так как х(2с) = 2bс(с – 2с/2) = 0, а при t > 2с сместится левее начала координат, так как x(t) < 0. Т.е. перемещение становится отрицательным. При этом путь S положителен:

.

Путь и перемещение совпадают лишь при t < с, т.е. при движении по прямой с неизменной по знаку скоростью.

Полученные результаты удобно проиллюстрировать графически. Построим графики зависимости (t), |(t)|, x(t), S(t) (см. рис. 2).

При t < с график пути S(t) совпадает с графиком x(t), который в свою очередь представляется параболой, а при t > с график S(t) получается из графика x(t) отражением его относительно прямой АА’, которая параллельна оси ОХ и проходит через точку А с ординатой bс²/2 (Почему? Подумайте сами. А в качестве подсказки советую еще раз посмотреть на полученные выражения для S(t) и (t)).

Мы решили задачу при условии положительности констант b и с. Разберитесь самостоятельно с характером движения тела, если b или с или обе эти величины отрицательны.