Задача 1

Шайба движется по гладкой горизонтальной плоскости и испытывает в точке 0 упругий удар с гладкой неподвижной стенкой. Найти точки, относительно которых момент импульса шайбы остается постоянным в этом процессе. Угол между направлением скорости шайбы и нормалью к стенке равен .

Решение

Движение шайбы представлено на рис.1. Так как стенка гладкая то F_тр = 0, и N – сила реакции при ударе направленная перпендикулярно стенке, ее момент равен нулю относительно любой точки, лежащей на прямой OO', перпендикулярной стенке.

Согласно уравнению моментов dL/dt = M. Так как относительно точек прямой ОО' момент силы реакции M= 0, то dL/dt = 0 и L = const. Итак, момент импульса шайбы сохраняется относительно любой точки, лежащей на прямой ОО'. Другие силы, действующие на шайбу, как нетрудно понять, не изменяют ее момента (разберитесь с этим сами).

Рис. 1

Задача 2

На гладкой горизонтальной плоскости лежат две небольшие одинаковые шайбы массы m каждая. Шайбы соединены друг с другом невесомой пружиной длины l₀ и жесткости k. В некоторый момент времени одной из шайб сообщили скорость v₀ в горизонтальном направлении, перпендикулярно пружине. Найти максимальное относительное удлинение пружины в процессе движения, если известно, что оно значительно меньше единицы.

Решение

Поскольку шайбы движутся по гладкой горизонтальной плоскости, то сумма внешних сил – силы тяжести и силы реакции стола, действующих на каждую шайбу, равна нулю, поэтому такая система ведет себя как замкнутая, и в ней сохраняются импульс и момент импульса. Кроме того, в системе действуют лишь консервативные силы (силы упругости пружины), поэтому сохраняется ее энергия.

Этих трёх законов сохранения достаточно, чтобы решить задачу. Удобнее всего делать это в системе отсчета, связанной с центром инерции. В этой системе отсчета сумма импульсов шайб равна нулю, откуда следует, что в любой момент времени скорости шайб равны по величине и направлены в противоположные стороны. Начальные скорости шайб относительно плоскости равны соответственно v₀ и нулю. Поэтому скорость центра инерции:

Скорости шайб по отношению к центру инерции равны, соответственно:

Причем скорости v₁ и v₂ направлены перпендикулярно пружине.

Так как в начальный момент времени пружина не деформирована, то энергия системы относительно ее центра масс определяется в этот момент лишь кинетической энергией частиц:

Момент импульса L₁ системы шайб относительно центра инерции в этот же момент времени равен:

Когда пружина окажется максимально растянутой, скорости шайб опять будут направлены перпендикулярно пружине, иначе шайбы удалялись бы или приближались друг к другу, т.е. длина пружины либо увеличивалась, либо уменьшалась бы, но, в любом из этих случаев, не была бы в этот момент максимальной. Если обозначить величину скорости шайб в этот момент через ', длину пружины в этот момент через l', то

В выражении для энергии второе слагаемое представляет собой потенциальную энергию растянутой на длину l’ – l₀ пружины.

В силу законов сохранения энергии и момента импульса имеем следующие уравнения:

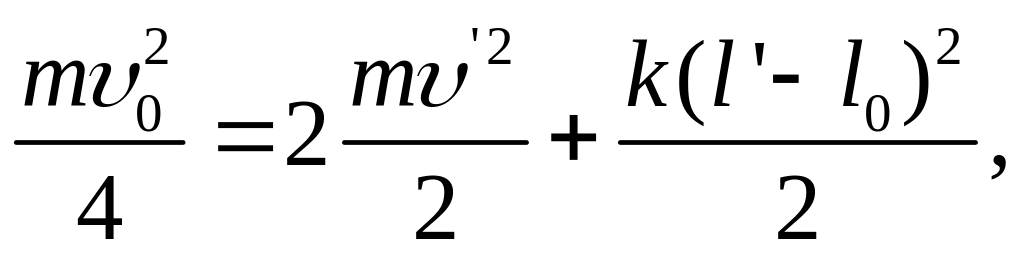
Выразив новую скорость шайб v’ из второго из этих уравнений, и подставив её в первое уравнение, найдём:

откуда приходим к уравнению:

После сокращения обеих частей уравнения на l’– l₀ получим:

а учитывая малую величину удлинения пружины (l’– l₀ << l₀), приходим к ответу:

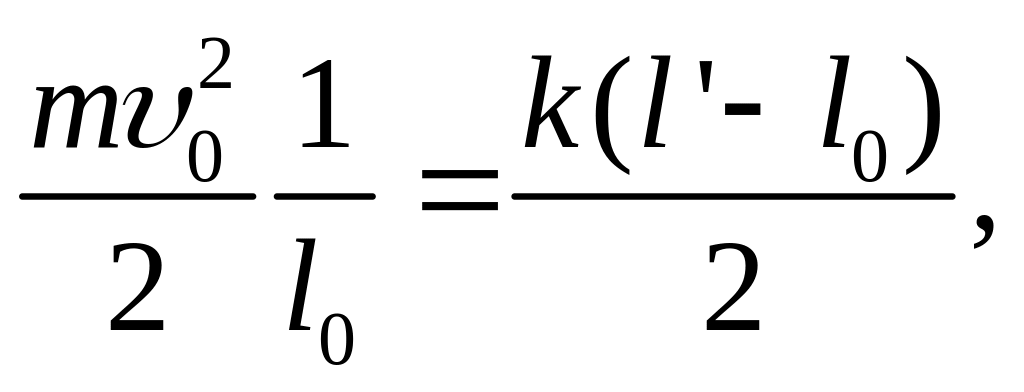
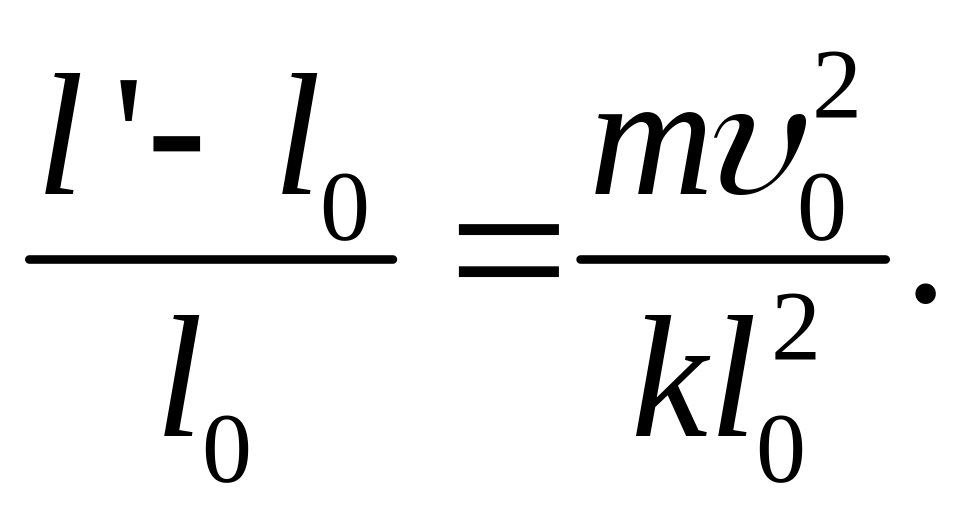
Из полученного ответа видно, что удлинение пружины будет малым, если выполнено неравенство: