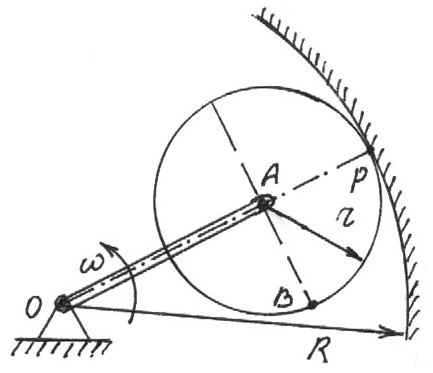
Приклад виконання завдання

Задача. Знайти швидкість точки В і прискорення точок В і Р рухомої шестерні радіуса r=0,05 м., яка котиться в середині нерухомої шестерні радіуса R=0,15 м. Шестерню радіуса r рухає кривошип, який обертається навколо осі О рівномірно з кутовою швидкістю =3 рад/с (рис. 2.4).

Рис. 2.4.

Д ано:

R=0,15 м

r=0,05 м

=3 рад/с

-?

-?

-?

Розв’язання

1. Аналіз руху механізму. Досліджуючи рух механізму бачимо, що кривошип ОА, рівномірно обертаючись навколо осі О, рухає шестерню, яка в свою чергу обертається навколо пальця кривошипу А. Рухома шестерня котиться в середині нерухомої шестерні без ковзання. Отже, рух малої шестерні є плоскопаралельний, а рух кривошипа обертальний навколо нерухомої осі.

2. Визначення швидкості точки В. Положення миттєвого центра швидкостей малої шестерні Р відоме за умовою і тому її плоский рух в даний момент часу можна розглядати як обертальний навколо миттєвого центра швидкостей Р (рис.2.5).

Рис2.5

Отже за законами розподілу швидкостей відносно миттєвого центра швидкостей дістанемо:

Звідки

(1)

Невідому швидкість точки А, можна знайти як швидкість точки кривошипа ОА:

м/с.

Вектор напрямлений перпендикулярно до ОА, а вектор М

перпендикулярно до ВР (рис.2.5). Модуль вектора знаходимо за формулою (1):

3. Визначення прискорень точок В і Р. Плоский рух малої шестерні складається з поступального руху разом з полюсом, точкою А, і обертальною навколо осі, що проходить через полюс А. Прискорення точок В і Р визначимо за теоремою про додавання прискорень точки у плоскому русі:

,

де за модулем

r; r. (2)

Спочатку визначимо прискорення полюса, точки А, як точки кривошипа ОА. Кривошип ОА обертається навколо осі О з сталою кутовою швидкістю. Отже, його кутове прискорення дорівнює нулю: Прискорення точки А кривошипа визначаються за формулою: де за модулем . Отже, прискорення точки А дорівнює

і напрямлене до центра обертання кривошипа О по радіусу ОА.

Визначимо кутову швидкість і кутове прискорення рухомої шестерні, необхідні для формул (2).

Миттєвий центр швидкостей знаходиться в точці Р, отже:

За умовою задачі , тому, що Таким чином ,згідно (2) модулі прискорень і дорівнюють

Вектори і напрямлені по радіусах до центра А рухомої шестерні (рис.2.5). Вектори і дорівнюють нулю, згідно формули (2), тому, що

Таким чином, прискорення точок В і Р знаходиться за формулами:

(3)

Як показано на рис.1.4, вектори прискорень і взаємно перпендикулярні і тому, згідно (3),

а вектори прискорень і паралельні і тому, згідно (3),

Відповідь:

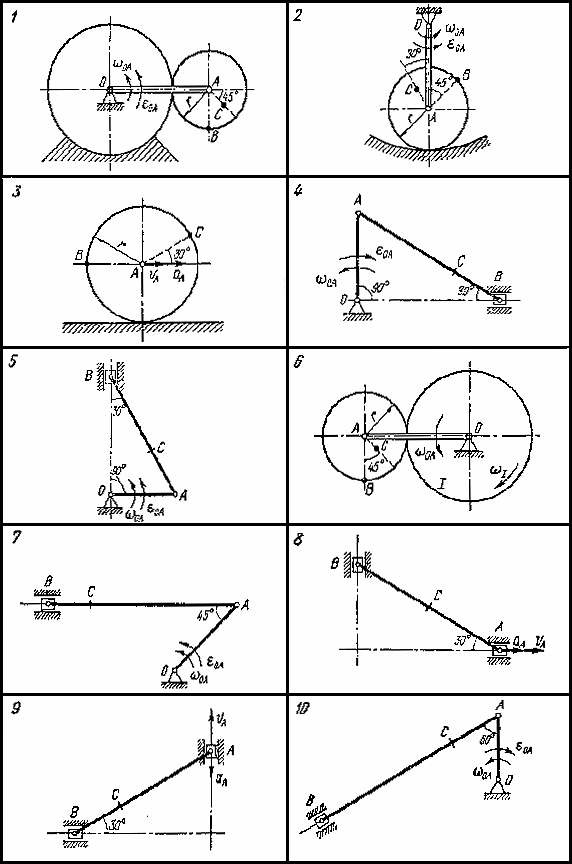
Таблиця 6

№ варианта	Розміри, см			wOA , рад/с	w1 , рад/с	eOA , рад/с2	VA , см/с	аA , см/с2
	ОА	r	AB
1	2	3	4	5	6	7	8	9
1	40	15	-	2	-	2	-	-
2	30	15	-	3	-	2	-	-
3	-	50	-	-	-	-	50	100
4	35	-	-	4	-	8	-	-
5	25	-	-	1	-	1	-	-
6	40	15	-	1	1	0	-	-
7	35	-	75	5	-	10	-	-
8	-	-	20	-	-	-	40	20
9	-	-	45	-	-	-	20	10
10	25	-	80	1	-	2	-	-

Рисунок 5