
1 ЦЕЛЬ РАБОТЫ
Освоить теорию надежности и приобрести навыки применения ее результатов к решению прикладных вопросов надежности автомобилей, автомобильного хозяйства и оборудования.
2 ОБЩИЕ ПОЛОЖЕНИЯ
Одним из факторов, сдерживающих повышение технического уровня автомобилей, автомобильного хозяйства и оборудования, является недостаточная надежность и отсутствие системы испытаний на надежность в процессе изготовления опытного образца и в серийном производстве. Затраты на техническое обслуживание и ремонт оборудования очень высоки. Без методов и расчетов на основе теории надежности трудно установить момент остановки оборудования на ремонт и обслуживание. Современные методы определения и контроля показателей надежности, а также средства испытаний оборудования на надежность, позволяют повысить технический уровень оборудования автомобилей и автомобильного хозяйства.
3 Основные понятия и определения
Основные понятия и определения надежности регламентированы стандартом. При изучении надежности технических устройств рассматриваются самые разнообразные объекты – машины, сооружения, аппаратура и др. В соответствии с государственными стандартами под понятием объект понимается предмет определенного назначения, рассматриваемый в период проектирования, производства, эксплуатации, исследований и испытаний на надежность.
Стандарт различает исправное и работоспособное состояние объекта. При исправном состоянии объект соответствует всем требованиям, установленным нормативно-технической документацией. В практике принято оценивать машины и оборудование не по исправному, а по работоспособному их состоянию. Одними из основных понятий в теории надежности являются:
Работоспособность – это состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения заданных параметров в пределах, установленных нормативно-технической документацией.
Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.
Повреждение – событие, заключающееся в нарушении исправного состояния объекта при сохранении им работоспособного состояния.
Сбой – самоустраняющийся отказ.
Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования.
Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки.
Долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.
Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов и повреждений, к поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонтов. Машины и оборудование лесного комплекса относятся к категории ремонтируемых машин.
Сохраняемость – свойство объекта сохранять работоспособность в течение и после установленного срока хранения или транспортирования.
4 ХАРАКТЕРИСТИКИ ОСНОВНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
4.1 БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
![]() (1.1)
(1.1)
где X – дискретная случайная величина; Pm – вероятность появления случайной величины; m = 0, 1, …, n; – возможные значения случайной величины; n – количество независимых опытов; p – вероятность появления ожидаемого события в каждом независимом опыте; 0< p <1; q = 1 – p.
Математическое ожидание, дисперсия и среднеквадратическое отклонение в соответствии с классическим определением имеют вид
![]() ,
(1.2)
,
(1.2)
![]() ,
(1.3)
,
(1.3)
![]() .
(1.4)
.
(1.4)
При использовании производящих функций формулы (1.2) и (1.3) можно представить в более простой записи
![]() ,
(1.5)
,
(1.5)
![]() .
(1.6)
.
(1.6)
Если вероятность появления ожидаемого события в каждом независимом опыте различна, то
![]() (1.7)
(1.7)
Задача
1. Из лесного
массива отправлено
![]() лесовозов на лесопильные рамы. Каждый
лесовоз может не доехать до места
назначения с вероятностью
лесовозов на лесопильные рамы. Каждый
лесовоз может не доехать до места
назначения с вероятностью
![]() независимо от других лесовозов. Значением
случайной величины Х здесь является
независимо от других лесовозов. Значением
случайной величины Х здесь является
![]() – число не доехавших лесовозов. Найти:
– число не доехавших лесовозов. Найти:
вероятность того, что до места назначения доедет не менее
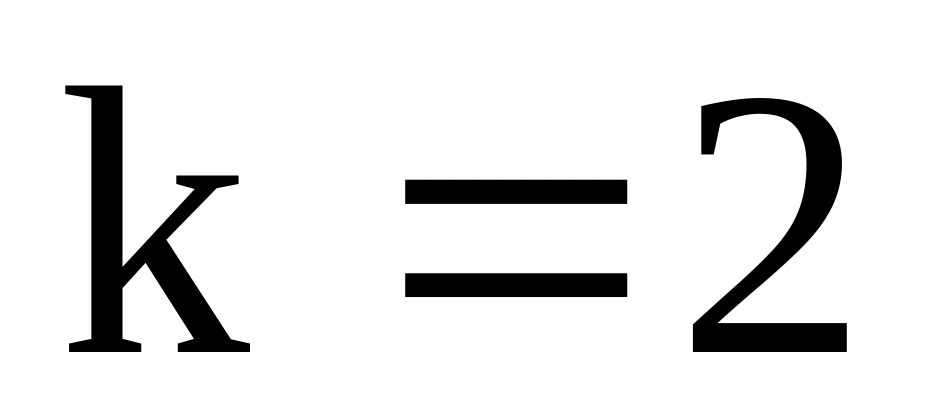 лесовозов;
лесовозов; – наиболее
вероятное число недоехавших лесовозов;
– наиболее
вероятное число недоехавших лесовозов;дисперсию и среднеквадратическое отклонение случайной величины Х.
Решение. Число недоехавших автомобилей распределено по биномиальному закону. По формуле (1.1) строим табл.1.1.
Таблица 1.1 – вероятности для различного количества недоехавших лесовозов
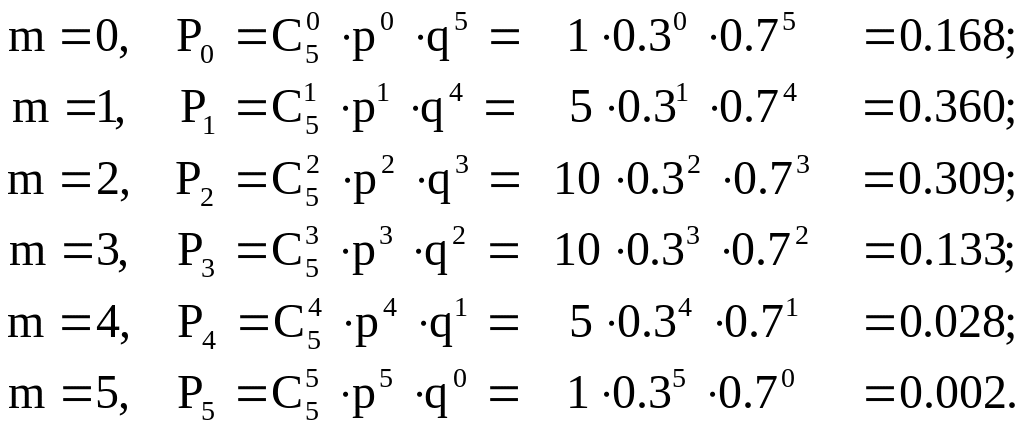
1) Вероятность того, что до места назначения доедет не менее двух лесовозов соответствует условию – до места назначения не доедет не более трех лесовозов. Используя данные табл. 1.1 запишем:
![]() .
.
2) Наиболее вероятное число недоехавших лесовозов соответствует математическому ожиданию случайной величины Х
![]() ,
,
т.е. наиболее вероятно: до места назначения не доедет от 1 до 2-х лесовозов.
3)
![]()
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
4.2 РАСПРЕДЕЛЕНИЕ ПУАССОНА
![]() ,
(2.1)
,
(2.1)
где X – дискретная случайная величина; Pm – вероятность появления случайной величины; m = 0, 1, 2,… – возможные значения случайной величины; а – параметр распределения Пуассона.
![]() .
(2.2)
.
(2.2)
Если
![]() ,
то
,
то
![]() ,
(2.3)
,
(2.3)
где
![]() – интенсивность потока событий; τ –
время.
– интенсивность потока событий; τ –
время.
Используя производящие функции можно показать, что математическое ожидание и дисперсия случайной величины с распределением Пуассона равны между собой:
![]() .
(2.4)
.
(2.4)
Задача
2. На станцию
технического обслуживания поступают
автомобили с интенсивностью
![]() авт./час. Найти вероятность того, что за
время τ=2 часа:
авт./час. Найти вероятность того, что за
время τ=2 часа:
не поступит ни одного автомобиля;
поступит ровно m1 автомобилей, m1=1;
поступит хотя бы m2 автомобилей, m2=1.
Решение. Интенсивность потока поступления автомобилей величина постоянная, поэтому воспользуемся формулой (2.3) для определения параметра распределения Пуассона, т.е.
![]() .
(2.5)
.
(2.5)
1)
Для события, что не поступит ни одного
автомобиля соответствует значение
![]() и, используя формулу (2.1) и (2.5), получим
вероятность этого события
и, используя формулу (2.1) и (2.5), получим
вероятность этого события
![]() .
.
2) Для события, что поступит ровно один автомобиль вероятность определиться следующим образом
![]() .
.
3)
![]() .
.
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Задача 3. На автозаправочную станцию с 0 ч до 6 ч 40мин прибывают автомобили с интенсивностью потока, линейно зависящего от времени, т.е.
![]() авт./мин.
(2.6)
авт./мин.
(2.6)
Поток прибытия автомобилей является пуассоновским нестационарным процессом. На основе статистических данных с учетом того, что 6 ч 40 мин = 400 мин дана интенсивность потока в начале и конце контролируемого временного интервала, т.е.
![]() авт/мин,
(2.7)
авт/мин,
(2.7)
![]() авт/мин.
(2.8)
авт/мин.
(2.8)
Найти
вероятность P того, что за интервал
времени от
![]() мин (3 ч 15 мин) до
мин (3 ч 15 мин) до
![]() мин (3 ч 25 мин) поступит не менее n=3
автомобилей.
мин (3 ч 25 мин) поступит не менее n=3
автомобилей.
Решение. Найдем значение коэффициентов В и С, входящих в формулу (2.6) из следующей системы уравнений
![]() ,
(2.9)
,
(2.9)
откуда В = 1/2000, С = 0.2. Воспользовавшись формулой (2.2), определим среднее число прибывших автомобилей в заданном интервале времени [195 мин, 205 мин]
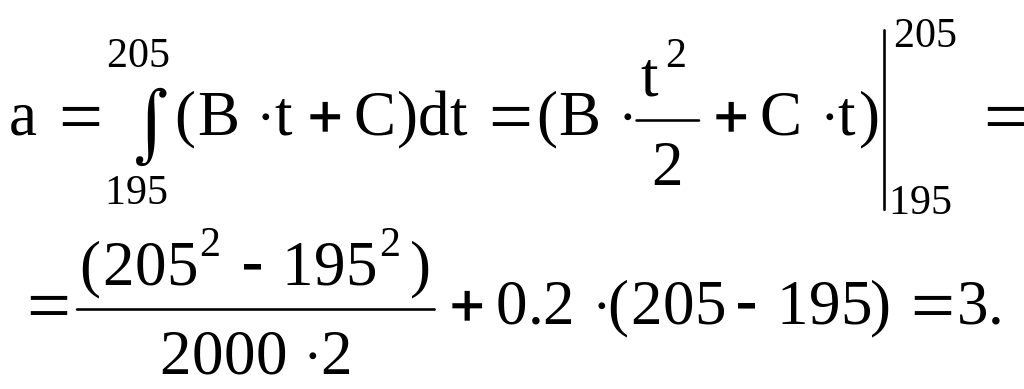
Искомая вероятность определится из следующего соотношения с использованием формулы (2.1)
![]()
Ответ:![]() .
.
