Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Южно-уральский институт управления и экономики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ответы Мат Методы.doc

Скачиваний:

Добавлен:

10.11.2019

Размер:

2.79 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Математическая модель транспортной задач

Переменными (неизвестными) транспортной задачи являются x_ij, i= 1, 2, …, m, j= 1, 2, …, n – объёмы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные можно записать в виде матрицы перевозок

х₁₁ х₁₂ … х₁_n

X = х₂₁ х₂₂ … х₂_n

… … … …

х_m₁ х_m₂ … х_mn

Так как произведение C_ijX_ij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны C_ijX_ij. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид

Z(X) = C_ij X_ij → min

Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:

X_ij = a_i, i = 1, 2, …, m.

Вторая группа из n уравнений выражает требование полностью

удовлетворить запросы всех n потребителей:

Z(X) = C_ij X_ij → min, (1)

X_ij= a_i, i = 1, 2, …, m, (2) X_ij = b_j, j = 1, 2, …, n, (3)

X_ij ≥ 0, i = 1, 2, …, m, j = 1, 2, …, n. (4)

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей,

т.е. a_i = b_j(5)

Такая задача называется задачей с правильным балансом, а её модель -закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а её модель – открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи

X = (x_ij), i = 1, 2, …, m, j = 1, 2, …, n,

Удовлетворяющие системе ограничений (2), (3), условиям неотрицательности (4), и обеспечивающее минимум целевой функции (1).

Математическая модель транспортной задачи может быть записана в векторном виде. Для этого рассмотрим матрицу А системы уравнений - ограничений задачи (2), (3).

х₁₁ х₁₂ … х₁_n х₂₁х₂₂… х₂_n… х_m₁ х_m₂ ... х_mn

1 1 … 1 0 0 … 0 … 0 0 ... 0

0 0 … 0 1 1 … 1 … 0 0 ... 0

………………………………………………………………………………………

А = 0 0 … 0 0 0 … 0 … 1 1 ... 1 (6)

1 0 … 0 1 0 … 0 … 1 0 ... 0

0 1 … 0 0 1 … 0 … 0 1 ... 0

………………………………………………………………………………………

0 0 … 1 0 0 … 1 … 0 0 ... 1

Сверху над каждым столбцом матрицы указана переменная задачи, коэффициентами при которой являются элементы соответствующего столбца в уравнениях системы ограничений. Каждый столбец матрицы А, соответствующий переменной X_ij, является вектором – условием задачи и обозначается через А_ij. Каждый вектор имеет всего m + n координат, и только две из них, отличные от нуля, равны единице. Первая единица вектора А_ij Стоит на i-м месте, а вторая – на (m + j)-м месте, т.е.

Номер координаты

0 1 a₁

…

1 i a_i

…

А_ij= 0 m ; A₀= a_m

0 m+1 b₁

…

1 m+j b_j

…

0 m+n b_n

Обозначим через A₀ вектор ограничений (правых частей уравнений (3), (3) и представим систему ограничений задачи в векторном виде. Тогда математическая модель транспортной задачи запишется следующим образом:

Z(x)= C_ijX_ij→min (7)

A_ijX_ij =A₀ (8)

X_ij≥0, i=1, 2, …, m, j=1, 2, …, n. (9)

Нахождение начального опорного решения транспортной задачи линейного программирования методом минимальной стоимости.

Метод минимальной стоимости

Метод минимальной стоимости прост, он позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C = (c_il), i = 1, 2, …, m, j = 1, 2, …, n. Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости (c_ij), и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую (c_ij), заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.

Теорема: Решение транспортной задачи, построенное методом минимальной стоимости, является опорным.

Нахождение начального опорного решения транспортной задачи линейного программирования методом северо-западного угла.

Метод северо-западного угла

Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла. В данном методе запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель. Осуществляется это таким образом:

если a_i < b_j, то x_ij = a_ij и исключается поставщик с номером i, x_ik = 0,

k = 1, 2, ..., n, k ≠ j, = b_j - a_i ;

если а_i. > Ь_j, то х_ij = b_j и исключается потребитель с номером j,

x_kj =0, k = 1, 2, ..., m, k ≠ i, = a_i - b_j ;

если a_i = b_j, то x_ij = a_i = b_j, и исключается либо i-й поставщик,

х_ik = 0, k = 1, 2, ..., n, k ≠ j, = 0 либо j-й потребитель, x_kj = 0,

k = 1, 2, ... m, k ≠ i, = 0.

Нулевые перевозки принято заносить в таблицу только тогда, когда они попадают в клетку (i, j), подлежащую заполнению. Если в очередную клетку таблицы (i, j) требуется поставить перевозку, а i-й поставщик или j-й потребитель имеет нулевые запасы или запросы, то в клетку ставится

перевозка, равная нулю (базисный нуль), и после этого, как обычно, исключается из рассмотрения соответствующий поставщик или потребитель.

Таким образом, в таблицу заносят только базисные нули, остальные клетки с нулевыми перевозками остаются пустыми.

Во избежание ошибок после построения начального опорного решения необходимо проверить, что число занятых клеток равно m + n - 1 и векторы-условия, соответствующие этим клеткам, линейно независимы.

Теорема: Решение транспортной задачи, построенное методом северо-западного угла, является опорным.

Оптимизация начального опорного решения транспортной ЗЛП методом потенциалов.

Широко распространенным методом решения транспортных задач является метод потенциалов. Этот метод позволяет упростить наиболее трудоемкую часть вычислений - нахождение оценок свободных клеток.

Теорема (признак оптимальности опорного решения).

Если допустимое решение X = (x_ij), i = 1, 2, ..., m, j = 1, 2, ..., n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков u_i, i = 1, 2, ..., m и потребителей v_j, j = 1, 2, ..., n удовлетворяющие следующим условиям:

u_i + v_j = c_ijпри x_ij > 0 (1)

u_i + v_j ≤ c_ij при x_ij = 0 (2)

Группа равенств (1) u_i + v_j = c_ijпри x_ij > 0 используется как система уравнений для нахождения потенциалов. Нетрудно видеть, что эта система могла иметь несколько другой вид, например -u_i + v_j = c_ij или u_i - v_j = c_ij, если перед тем, как записать двойственную задачу, все уравнения одной из групп уравнений исходной задачи умножить на (-1).

Данная система уравнений имеет m+ n неизвестных u_i, i = 1, 2, ..., т, и v_j, j = 1, 2, ..., n. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m + m - 1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы.

Группа неравенств (2) u_i + v_j ≤ c_ij при x_ij = 0 используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде

Δ_ij = u_i + v_j – c_ij ≤ 0 при x_ij = 0 (3)

Числа Δ_ij называются оценками свободных клеток таблицы или векторов-условий транспортной задачи, не входящих в базис опорного решения. В этом случае признак оптимальности можно сформулировать так же, как в симплексном методе (для задачи на минимум): опорное решение является оптимальным, если для всех векторов-условий (клеток таблицы) оценки неположительные.

Оценки для свободных клеток транспортной таблицы используются для улучшения опорного решения. С этой целью находят клетку (I, k) таблицы, соответствующую max {Δ_ij} = Δ_Ik. Если Δ_Ik ≤ 0, то решение оптимальное. Если же Δ_Ik > 0, то для соответствующей клетки (I, k) строят цикл и улучшают решение, перераспределяя груз Ө = {x_ij} по этому циклу.

Алгоритм решения транспортной задачи методом потенциалов следующий.

1 Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.

2 Строят начальное опорное решение (методом минимальной стоимости или каким-либо другим методом) и проверяют правильность его построения, для чего подсчитывают количество занятых клеток (их должно быть m+n-1) и убеждаются в линейной независимости векторов-условий (методом вычеркивания).

3 Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений + = при >0. Для того чтобы

найти частное решение системы, одному из потенциалов (обычно тому, которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам

= - при >0,

если известен потенциал , и

= - при >0,

если известен потенциал .

4 Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам = + - и те оценки, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток 0, то вычисляют значение целевой функции, и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным.

5 Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка max{ }= . Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину Ө = {x_ij}. Клетка со знаком «-», в которой достигается Ө = {x_ij} , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m+n-1.

Нелинейное программирование.

предположение о возможности описать зависимости между управляемыми переменными с помощью линейных функций далеко не всегда адекватно природе моделируемого объекта. Например, в рассмотренных в главе 1 моделях цена товара считается независимой от количества произведенного продукта, однако в повседневной жизни мы постоянно сталкиваемся с тем, что она может зависеть от объема партии товара. Аналогичные замечания могут быть сделаны и по поводу технологических ограничений: расход определенных видов сырья и ресурсов происходит не линейно, а скачкообразно (в зависимости от объема производства). Попытки учесть эти факторы приводят к формулировке более общих и сложных оптимизационных задач. Изучение методов их решения составляет предмет научной области, получившей названия нелинейного программирования.

Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции f(x_{, х₂,..., х_п) на множестве D, определяемом системой ограничений

(2.1)

где хотя бы одна из функций f или g_i является нелинейной.

По аналогии с линейным программированием ЗНП однозначно определяется парой (D,f) и кратко может быть записана в следующем виде

(2.2)

Также очевидно, что вопрос о типе оптимизации не является принципиальным. Поэтому мы, для определенности, в дальнейшем по умолчанию будем рассматривать задачи максимизации.

Как и в ЗЛП, вектор называется допустимым планом, а если для любого xD выполняется неравенство , то х^* называют оптимальным планом. В этом случае х^* является точкой глобального максимума.

С точки зрения экономической интерпретации f(x) может рассматриваться как доход, который получает фирма (предприятие) при плане выпуска х, а как технологические ограничения на возможности выпуска продукции. В данном случае они являются обобщением ресурсных ограничений в ЗЛП

Задача (2.2) является весьма общей, т. к. допускает запись логических условий, например:

или запись условий дискретности множеств:

Набор ограничений, определяющих множество D, при необходимости всегда можно свести либо к системе, состоящей из одних неравенств:

либо, добавив фиктивные переменные у, к системе уравнений:

Перечислим свойства ЗИП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования:

1. Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным).

2. Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов).

3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа.

В силу названных факторов задачи нелинейного программирования настолько разнообразны, что для них не существует общего метода решения.

Решение задач условной оптимизации методом Лагранжа. Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа. Многим читателям он должен быть известен из курса дифференциального исчисления. Идея данного метода состоит в сведении задачи поиска условного экстремума целевой функции

(2.3)

на множестве допустимых значения D, описываемом системой уравнений

(2.4)

к задаче безусловной оптимизации функции

Ф(x,u) = f(x₁,x₂,...,x_n)+u_lg_l(xi,x₂,...,x_n)+...+u_ng_m(x_l,x₂,...,x_n), (2.5)

где — вектор дополнительных переменных, называемых множителями Лагранжа. Функцию Ф(х,и), где , , называют функцией Лагранжа. В случае дифференцируемое™ функций f и g_i справедлива теорема, определяющая необходимое условие существования точки условного экстремума в задаче (2.3)-(2.4). Поскольку она непосредственно относится к предмету математического анализа, приведем ее без доказательства.

Теорема 2.1. Если х^* является точкой условного экстремума функции (2.3) при ограничениях (2.4) и ранг матрицы первых частных производных функций

равен т, то существуют такие , не равные одновременно нулю, при которых

(2.6)

Из теоремы (2.1) вытекает метод поиска условного экстремума, получивший название метода множителей Лагранжа, или просто метода Лагранжа. Он состоит из следующих этапов.

1. Составление функции Лагранжа Ф(х,и).

2. Нахождение частных производных

3. Решение системы уравнений

(2.7)

относительно переменных х и и.

4. Исследование точек, удовлетворяющих системе (2.7), на максимум (минимум) с помощью достаточного признака экстремума.

Присутствие последнего (четвертого) этапа объясняется тем, что теорема (2.1) дает необходимое, но не достаточное условие экстремума. Положение дел с достаточными признаками условного экстремума обстоит гораздо сложнее. Вообще говоря, они существуют, но справедливы для гораздо более частных ситуаций (при весьма жестких предпосылках относительно функций f и g_i) и, как правило, трудноприменимы на практике. Еще раз подчеркнем, что основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных средств решения проблемы. Однако нетрудно заметить, что задача решения системы уравнений (2.7), к которой сводится данный метод, в общем случае не проще исходной проблемы поиска экстремума (2.3)-(2.4). Методы, подразумевающие такое решение, называются непрямыми. Они могут быть применены для весьма узкого класса задач, для которых удается получить линейную или сводящуюся к линейной систему уравнений (2.7). Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.

Градиентные методы решения задач безусловной оптимизации. Ведущее место среди прямых методов решения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационарных точек дифференцируемой функции. Напомним, что стационарной называется точка, в которой и которая в соответствии с необходимым условием оптимальности является «подозрительной» на наличие локального экстремума. Таким образом, применяя градиентный метод, находят множество точек локальных максимумов (или минимумов), среди которых определяется максимум (или минимум) глобальный.

Идея данного метода основана на том, что градиент функции указывает направление ее наиболее быстрого возрастания в окрестности той точки, в которой он вычислен. Поэтому, если из некоторой текущей точки х⁽¹⁾ перемещаться в направлении вектора , то функция f будет возрастать, по крайней мере, в некоторой окрестности х⁽¹⁾. Следовательно, для точки , , лежащей в такой окрестности, справедливо неравенство . Продолжая этот процесс, мы постепенно будем приближаться к точке некоторого локального максимума (см. рис. 2.1).

Однако как только определяется направление движения, сразу же встает вопрос о том, как далеко следует двигаться в этом направлении или, другими словами, возникает проблема выбора шага , в рекуррентной формуле

(2.8)

задающей последовательность точек, стремящихся к точке максимума.

В зависимости от способа ее решения различают различные варианты градиентного метода. Остановимся на наиболее известных из них.

Метод наискорейшего спуска

Название метода можно было бы понимать буквально, если бы речь шла о минимизации целевой функции. Тем не менее, по традиции такое название используется и при решении задачи на максимум.

Пусть f(x) = f(x_l,x_l,...x_n) — дифференцируемая функция, заданная на Rⁿ, а — некоторая текущая точка. Оговоримся, что каких-либо общих рекомендаций, касающихся выбора исходной точки (или, как еще говорят, начального приближения) x⁽⁰⁾, не существует, однако по возможности она должна находиться близко от искомого оптимального плана х^*. Как уже говорилось выше, если x⁽^q⁾ — нестационарная точка (т. е. ), то при движении в направлении функция f(x) на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продолжалось до тех пор, пока возрастание не прекратится. Для этого выразим зависимость значения f(x) от шагового множителя  > 0 , полагая

(2.9)

или, в координатной форме,

(2.10)

Чтобы добиться наибольшего из возможных значений f при движении по направлению , нужно выбрать такое значение , которое максимизирует функцию . Для вычисления , используется необходимое условие экстремума . Заметим, что если для любого  >0 , то функция f(x) не ограничена сверху (т. е. не имеет максимума). В противном случае, на основе (2.10) получаем

(2.11)

что, в свою очередь, дает

(2.12)

Если считать, что следующая точка соответствует оптимальному значению , то в ней должно выполняться условие , и следует находить из условия или

(2.13)

Условие (2.13) означает равенство нулю скалярного произведения градиентов функции f точках х⁽^q⁺¹⁾ и х⁽^q⁾ Геометрически оно может быть интерпретировано как перпендикулярность векторов градиентов функции f в указанных точках, что и показано на рис. 2.2. Продолжая геометрическую интерпретацию метода наискорейшего спуска, отметим, что в точке х⁽^q⁺¹⁾ вектор , будучи градиентом, перпендикулярен линии уровня, проходящей через данную точку. Стало быть, вектор является касательным к этой линии. Итак, движение в направлении градиента следует продолжать до тех пор, пока он пересекает линии уровня оптимизируемой функции.

После того как точка х⁽^q⁺¹⁾ найдена, она становится текущей для очередной итерации. На практике признаком достижения стационарной точки служит достаточно малое изменение координат точек, рассматриваемых на последовательных итерациях. Одновременно с этим координаты вектора должны быть близки к нулю.

Метод дробления шага

Для нахождения шага , в методе наискорейшего спуска требуется решить уравнение (2.13), которое может оказаться достаточно сложным. Поэтому часто ограничиваются «подбором» такого значения , что . Для этого задаются некоторым начальным значением ₁ (например, ₁ =1) и проверяют условие . Если оно не выполняется, то полагают

и т. д. до тех пор, пока не удается найти подходящий шаг, с которым переходят к следующей точке х⁽^q⁺¹⁾. Критерий завершения алгоритма, очевидно, будет таким же, как и в методе наискорейшего спуска.

Общий вид задач нелинейного программирования.

Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Допустим что среди ограничений нет неравенств. Не обязательны условия неотрицательности. Переменные не являются дискретными, m < n, функции и f(X) непрерывны и имею т частные производные по крайней мере второго порядка. В этом случае задачу оптимизации можно сформулировать так: найти переменные х₁, х₂,…,х_n, удовлетворяющие системе уравнений (1)

и обращающее в максимум (минимум) целевую функцию z = f(х₁, х₂,…,х_n). (2)

такие задачи можно решать классическими методами дифференциального исчисления. Однако, на этом пути встречаются такие вычислительные трудности, которые делают необходимым поиск других методов решения. Поэтому классические методы часто используются не в качестве вычислительного средства, а как основа для теоретического анализа.

Примером типичной и простой нелинейной задачи является следующая: данное предприятие для производства какого-то продукта расходует два средства в количестве х₁ и х₂ соответственно. Это факторы производства, например мамашины и труд, два различных вида сырья и т.п., а величины х₁ и х₂ – затраты факторов производства. Факторы производства впредь будем считать взаимозаменяемыми. Если это «труд» и «машины», то можно применять такие методы производства, при которых величина затрат машин в сопоставлении с величиной затрат труда больше или меньше (производство более или менее трудоемкое). В сельском хозяйстве взаимозаменяемыми факторами могут быть посевные площади или минеральные удобрения (экстенсивный или интенсивный метод производства).

Объем производства (выраженный в натуральных или стоимостных единицах) является функцией затрат производства z = f(х_1, х₂). Эта зависимость называется производственной функцией. Издержки зависят от расхода обоих факторов (х₁ и х₂) и от этих факторов (с₁ и с₂). Совокупные издержки выражаются формулой b = c₁ х₁ + c₂ х₂. требуется при данных совокупных издержках определить такое количество факторов производства. Которое максимизирует объем продукции z.

Математическая модель этой задачи имеет вид: определить такие переменные х₁ и х₂, удовлетворяющие условиям

(3) c₁ х₁ + c₂ х₂ = b,

х₁ , х₂ , при которых функция (4) z = f(х_1, х₂) достигает максимума.

Как правило, функция (4) может иметь произвольный нелинейный вид.

Пример решения ЗНП методом допустимых направлений. Рассмотрим процесс применения метода допустимых направлений на конкретном примере. Пусть дана ЗНП:

(2.26)

(2.27)

Итерация 1. В качестве начального приближения возьмем точку х⁽¹⁾ = (0,0). Нетрудно заметить, что она удовлетворяет системе неравенств (2.27), т. е. . Для х⁽¹⁾ все неравенства выполняются как строгие, т. е. множество индексов активных ограничений . Следовательно, в х⁽¹⁾ любое направление является допустимым, и нам остается определить, с каким шагом , можно двигаться вдоль градиента целевой функции . Система неравенств типа (2.18), из решения которых определяется интервал допустимых значений для , для данной задачи примет вид:

Тогда

достигается при . Отсюда получаем следующую точку

Итерация 2. Путем подстановки координат точки х⁽²⁾ в (2.27) определим множество активных ограничений в точке . Соответственно, задача (2.24) - (2.25), которую требуется решить для определения допустимого прогрессивного направления s⁽²⁾ с учетом того, что и , примет вид:

В данном случае оптимальный план ЗЛП находится довольно просто и равен . Отбросив дополнительную переменную , получаем вектор s⁽²⁾ = (1,0), т. е. очередная точка будет определяться как

Действуя по аналогии с предыдущей итерацией, для определения промежутка допустимых значений шагового множителя составляем систему неравенств (2.18):

Окончательно имеем .

Тогда

достигается при . Отсюда получаем следующую точку x⁽³⁾ = (3,4).

Итерация 3. В точке х⁽³⁾ множество активных ограничений будет иметь вид . Найдем значения градиентов: , и .

Задача определения допустимого прогрессивного направления (2.24)-(2.25) будет иметь вид:

Значение т из практических соображений следует брать достаточно малым, например  = 0,001 . Опуская решение данной задачи, приведем интересующие нас компоненты ее оптимального плана: s⁽³⁾ = (0,0). Итак, не существует прогрессивного направления, исходящего из точки х⁽³⁾. Таким образом, оптимальный план рассматриваемой задачи (2.26)-(2.27) х^* = (4,3), а максимальное значение целевой функции .

Графическая иллюстрация проведенного процесса решения представлена графически на рис.

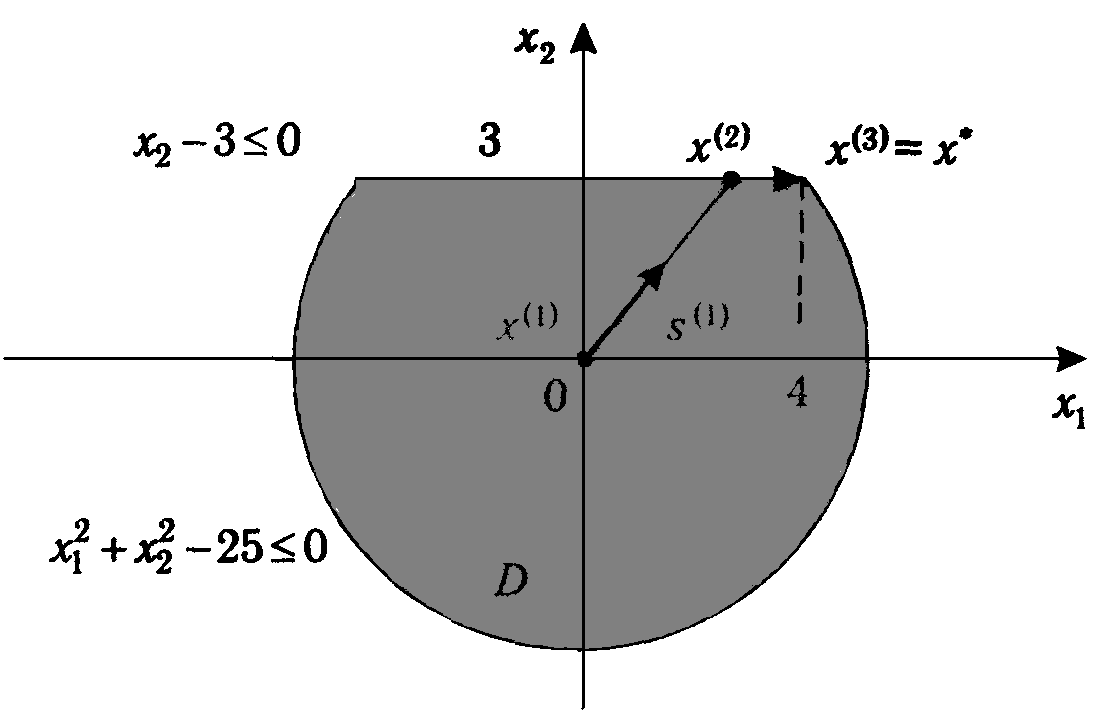
Рис.

Графический метод решения задач нелинейного программирования.

Пусть дана система неравенств вида (1) и функция (2), причем все функции являются выпуклыми на некотором выпуклом множестве М, а функция Z либо выпукла на множестве М, либо вогнута. Задача выпуклого программирования (ВП) состоит в отыскании такого решения системы ограничений (1), при котором целевая функция Z достигает минимального значения, или вогнутая функция Z достигает максимального значения. (Условия неотрицательности переменных можно считать включенными в систему(1)).

Всякая задача линейного программирования является частным случаем задачи ВП. В общем случае задачи являются задачами нелинейного программирования. Выделение задач ВП в специальный класс объясняется экстремальными свойствами выпуклых функций: всякий локальный минимум выпуклой функции (локальный максимум вогнутой функции) является одновременно и глобальным; кроме того, выпуклая (вогнутая) функция, заданная на замкнутом ограниченном множестве, достигает на этом множестве глобального минимума. Отсюда вытекает, что если целевая функция Z является строго выпуклой (строго вогнутой) и если область решений системы ограничений не пуста и ограничена, то задача ВП всегда имеет единственное решение. В этом случае минимум выпуклой (максимум вогнутой) функции достигается внутри области решений, если там имеется стационарная точка, или на границе этой области, если внутри нее нет стационарной точки. (В общем случае можно утверждать лишь, что множество оптимальных решений любой задачи ВП является выпуклым множеством).

Задача: геометрически решить следующую задачу ВП: найти минимум функции при ограничениях:

Решение: Строим область допустимых решений данной задачи:

а). - окружность с центром в начале координат и радиусом R = 2 (рис.1). область решений неравенства состоит из точек, лежащих внутри этой окружности и на ней самой;

б). - прямая, которую можно построить, например по точкам (0,0) и (2,1). Область решений неравенства - полуплоскость, лежащая над этой прямой, включая и саму прямую;

в). - прямая, которая строится, например по точкам (0,0) и (1,2). Область решений неравенства - полуплоскость, лежащая под этой прямой, включая и саму прямую. Таким образом, с учетом условий неотрицательности переменных, областью допустимых решений данной задачи является замкнутый сектор ОАВ (рис.1).

Теперь построим линию уровня функции Z и определим направление убывания Z. Все линии уровня имеют уравнение Z=C, т.е. .При С = 3 получаем линию уровня - это окружность с центром в точке О₁(1,1) и радиусом R = 1.Ясно, что в любой точке этой линии уровня при перемещении от центра окружности О₁ функция Z возрастает, а при перемещении к центру – убывает. Таким образом, минимум Z достигается в точке (1,1), Z_min = 2 (нетрудно убедиться, что точка (1,1) является стационарной точкой функции Z).

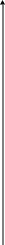
Х₂

Рси.1

О₁

Х₁

х₁=2х₂

х₂=2х₁

Динамическое программирование.

Динамическое программирование — раздел математического программирования, совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого решения и выработке оптимальной стратегии для последующих решений.

Процессы принятия решений, которые строятся по такому принципу, называются м но г о ш а г о в ы м и процессами. Математически оптимизационная задача строится с помощью таких соотношений, которые последовательно связаны между собой: например, полученный результат для одного года вводится в уравнение для следующего (или, наоборот, для предыдущего) и т. д. Таким образом, можно получить на вычислительной машине результаты решения задачи для любого избранного момента времени и «следовать» дальше. Динамическое программирование применяется не обязательно для задач, связанных с течением времени. Многошаговым может быть и процесс решения вполне статической задачи. Таковы, например, некоторые задачи распределения ресурсов.

Общим для задач динамического программирования является то, что переменные рассматриваются не вместе, а последовательно, одна за другой. Сущность состоит в том, что строится такая вычислительная схема, когда вместо одной задачи со многими переменными строится много задач с малым числом переменных (обычно даже одной) в каждой. Это значительно сокращает объем вычислений. Однако такое преимущество достигается лишь при двух условиях: когда критерий оптимальности аддитивен, т. е. общее оптимальное решение является суммой оптимальных решений каждого шага, и когда будущие результаты не зависят от предыстории того состояния системы, при котором принимается решение. Это вытекает из принципа оптимальности Беллмана, лежащего в основе теории динамического программирования. Из него же вытекает основной прием — нахождение правил доминирования, на основе которого на каждом шаге производится сравнение вариантов будущего развития и заблаговременное отсеивание заведомо бесперспективных вариантов. Когда эти правила обращаются в формулы, однозначно определяющие элементы последовательности один из других,' их называют разрешающими правилами. Несмотря на выигрыш в сокращении вычислений, их объем остается очень большим.

Можно выделить два наиболее общих класса задач, к которым в принципе мог бы быть применим этот метод, если бы не «проклятие размерности» (на самом деле на таких задачах, взятых в крайне упрощенном виде, пока удается лишь демонстрировать общие основы метода и анализировать экономико-математические модели). Первый — задача планирования деятельности экономического объекта (предприятия, отрасли и т. п.) с учетом изменения потребности в производимой продукции во времени. Второй класс задач — оптимальное распределение ресурсов между различными направлениями во времени. Сюда можно отнести, в частности, такую задачу: как распределить урожай зерна каждого года на питание и на семена, чтобы за ряд лет получить наибольшее количество хлеба?

Особенно эффективно применяется динамическое программирование тогда, когда по самому существу задачи приходится принимать решения по этапам. Покажем это на простом примере задачи ремонта и замены оборудования. На литейной машине шинного завода изготавливаются одновременно две шины — в двух формах. Если одна форма выходит из строя, машину приходится разбирать. При этом может оказаться выгодным заменить также и вторую форму, чтобы лишний раз не разбирать машину, если и эта форма выйдет из строя на следующем этапе. Более того, бывает, что есть смысл заменить обе формы до того, как одна из них выйдет из строя. Методом динамического программирования (с помощью дерева решений) определяется наилучшая стратегия в вопросе о замене форм с учетом всех факторов: выгоды от продолжения эксплуатации формы, потерь от простоя машины, стоимости забракованных шин и т. д.

Основные понятия динамического программирования.

Общая постановка и алгоритм решения задач методом динамического программирования. Будем считать, что состояние х^(к) рассматриваемой системы S на k-м шаге {к- 1, 2, ..., n) определяется совокупностью чисел х^(к) = ( , ,…, ),которые получены в результате реализации управления m_k, обеспечивающего переход системы S из состояния х^(к-1) в состояние х^(к).

Пусть также выполняются два условия:

1. Условие отсутствия последействия. Состояние х^(к) , в которое перешла система S, зависит от исходного состояния х^(к-1) и выбранного управления m_k, и не зависит от того, каким образом система S перешла в состояние х^(к-1).

2. Условие аддитивности. Если в результате реализации k-го шага обеспечен определенный доход G _k(x₍_k_-1) , m_k ), также зависящий от исходного состояния системы х⁽^k^-1) и выбранного управления m_k, то общий доход за n шагов составит , где m = (m₁, m₂,..., m_k)

Задача состоит в нахождении оптимальной стратегии управления, т. е. такой совокупности управлений m* = (m₁*, m₂*,..., m_k*),в результате реализации которых система S за n шагов переходит из начального состояния S_s= x⁽⁰⁾ в конечное S_f = x⁽ⁿ⁾ и при этом функция дохода G(m) принимает наибольшее значение.

Принцип оптимальности Беллмана. Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы доход на данном шаге плюс оптимальный доход на всех последующих шагах был максимальный.

Из принципа оптимальности следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т. д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, n-м шаге. Для того чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление , обеспечивающее максимальное значение функции дохода . Такое управление, выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.

Чтобы построить алгоритм решения задач, дадим математическую формулировку принципа оптимальности. Для этого введем некоторые дополнительные обозначения. Обозначив через максимальный доход, получаемый за n шагов при переходе системы S из начального состояния х⁽⁰⁾ в конечное состояние x⁽ⁿ⁾ при реализации оптимальной стратегии управления m* = (m₁*, m₂*,..., m_k*), а через F (x⁽^k⁾ ) — максимальный доход, получаемый при переходе из любого состояния х⁽^k⁾ в конечное состояние х⁽ⁿ⁾при оптимальной стратегии управления на оставшихся (n - к) шагах. Тогда

(1)

(2)

при к = 0, 1,2, ..., n - 1.

Выражение (2) представляет собой математическую запись принципа оптимальности Беллмана и носит название основного функционального уравнения Беллмана. Используя уравнение (2) находится решение рассматриваемой задачи динамического программирования. Рассмотрим этот процесс более подробно.

Полагая к = n- 1 в уравнении Беллмана (2), получаем следующее функциональное уравнение: (3)

В (3) можно считать известным. Используя теперь уравнение (3) и рассматривая всевозможные допустимые состояния системы S на (n - 1)-м шаге , ..., находим условные оптимальные решения и соответствующие значения функции (3):

Таким образом, на п-и шаге находим условно оптимальное управление при любом допустимом состоянии системы после (n - 1)-го шага, т. е. в каком бы состоянии система не оказалась после (n - 1)-го шага, нам уже известно, какое следует принять решение на n-м шаге.

Перейдем теперь к рассмотрению функционального уравнения при к = n – 2: (4)

Решая функциональное уравнение (4) при различных состояниях на (n - 2)-м шаге, получим условно оптимальные управления . Каждое из этих управлений совместно с уже выбранным управлением на последнем шаге обеспечивает максимальное значение дохода на двух последних шагах.

Последовательно осуществляя описанный выше итерационный процесс, дойдем до первого шага. На этом шаге известно, в каком состоянии может находиться система. Поэтому уже не требуется делать предположений о допустимых состояниях системы, а остается лишь только выбрать управление, которое является наилучшим с учетом условно оптимальных управлений, уже принятых на всех последующих шагах.

Чтобы найти оптимальную стратегию управления, т. е. определить искомое решение задачи, нужно теперь пройти всю последовательность шагов, только на этот раз от начала к концу. На первом шаге в качестве оптимального управления возьмем найденное условно оптимальное управление . На втором шаге найдем состояние , в которое переводит систему управление . Это состояние определяет найденное условно оптимальное управление , которое теперь будем считать оптимальным. Зная , находим , значит, определяем и т. д. В результате этого находим решение задачи, т. е. максимально возможный доход и оптимальную стратегию управления, включающую оптимальные управления на отдельных шагах.

Общая постановка задачи динамического программирования.

Пусть также выполняются два условия:

(1)

(2)

при к = 0, 1,2, ..., n - 1.

Полагая к = n- 1 в уравнении Беллмана (2), получаем следующее функциональное уравнение: (3)

Перейдем теперь к рассмотрению функционального уравнения при к = n – 2: (4)

Принцип оптимальности Беллмана.

Принцип оптимальности впервые был сформулирован Р. Беллманом в 1953 г. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование – процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломанной линии, то любая часть этой ломанной будет являться оптимальной траекторией относительно начала и конца.

Уравнения Беллмана. Рассмотрим последовательность задач, полагая последовательно n = 1,2,… при различных s – одношаговую, двухшаговую и т.д., - используя принцип оптимальности.

На каждом шаге любого состояния системы s_k_-1 решение X_k нужно выбирать «с оглядкой», так как этот выбор влияет на последующее состояние s_k и дальнейший процесс управления, зависящий от s_k_.это следует из принципа оптимальности.

Но есть один шаг, последний который можно для любого состояния s_n_-1 планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим n-й шаг: s_n_-1– состояние системы к началу n-го шага, - конечное состояние, X_n – управление на n-м шаге, а - целевая функция (выигрыш) n-го шага.

Согласно принципу оптимальности, X_nнужно выбирать так, чтобы для любых состояний s_n_-1 получить максимум целевой функции на этом шаге.

Обозначим через максимум целевой функции – показателя эффективности n-го шага при условии, что к началу последнего шага система S была в произвольном состоянии s_n_-1, а на последнем шаге управление было оптимальным.

называется условным максимумом целевой функции на n-м шаге. Очевидно, что (1)

Максимизация ведется по всем допустимым управлениям X_n. Решение X_n, при котором достигается , также зависит от s_n_-1 и называется оптимальным управлением на n-м шаге. Оно обозначается через .

Решив одномерную задачу локальной оптимизации (1), найдем для всех возможных состояний s_n_-1две функции и .

Рассмотрим пошаговую задачу: присоединим к n-му шагу (n-1)-й.(см. рис.).

условно оптимальный выигрыш на n-м шаге

значение целевой функции (n-1)-го шага при произвольном управлении Х_n_-1и состоянииS_n_-2

Для любых состояний s_n_-2 , произвольных управлений и оптимальном управлении на n-м шаге значение целевой функции на двух последних шагах равно: (2).

Согласно принципу оптимальности для любых s_n_-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем шаге (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (2) по всем допустимым управлениям . Максимум этой суммы зависит от s_n_-2, обозначается через и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. Соответствующее управление на (n-1) шаге обозначается через и называется условным оптимальным управлением на (n-1) шаге.

(3)

Выражение, входящее в фигурных скобках (3), зависит только от s_n_-2 и , так как s_n_-1 можно найти при k=n-1. и подставить вместо s_n_-1 в функцию .

В результате максимизации только по одной переменной согласно уравнению (3) вновь получается две функции: и .

Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется (n-2)-й и т.д.

Обозначим через условный максимум целевой функции, полученный при оптимальном управлении на n-k+1 шагах, начиная с к-го до конца, при условии, что к началу к-го шага система находилась в состоянии s_к-1.Фактически этафункция равна , тогда .

Целевая функция на n-k последних шагах при произвольном управлении Х_к на к-м шаге и оптимальном управлении на последующих n-k шагах равна . Согласно принципу оптимальности, Х_к выбирается из условия максимума этой суммы, т.е. (4), k=n-1,n-2,…,2,1.

Уравнение Х_кна к-м шаге, при котором достигается максимум, обозначается через и называется условным оптимальным управлением на к-м шаге в правую часть уравнения (4) следует вместо s_k подставить выражение . Уравнения (4) называют уравнениями Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущее значение функции, зная последующие.

Процесс решения уравнений (1) – (4) называется условной оптимизацией.

Общая идея метода динамического программирования.

Основные идеи вычислительного метода динамического программирования. Некоторые задачи математического программирования обладают специфическими особенностями, которые позволяют свести их решение к рассмотрению некоторого множества более простых «подзадач». В результате вопрос о глобальной оптимизации некоторой функции сводится к поэтапной оптимизации некоторых промежуточных целевых функций. В динамическом программировании^¹ рассматриваются методы, позволяющие путем поэтапной (многошаговой) оптимизации получить общий (результирующий) оптимум.

Обычно методами динамического программирования оптимизируют работу некоторых управляемых систем, эффект которой оценивается аддитивной, или мультипликативной, целевой функцией. Аддитивной называется такая функция нескольких переменных f(x₁ x₂,...,x_n), значение которой вычисляется как сумма некоторых функций f_j, зависящих только от одной переменной x_j:

(1)

Слагаемые аддитивной целевой функции соответствуют эффекту решений, принимаемых на отдельных этапах управляемого процесса. По аналогии, мультипликативная функция распадается на произведение положительных функций различных переменных:

(2)

Поскольку логарифм функции типа (2) является аддитивной функцией, достаточно ограничиться рассмотрением функций вида (1).

Изложим сущность вычислительного метода динамического программирования на примере задачи оптимизации

(3)

при ограничениях

(4)

Отметим, что в отличие от задач, рассмотренных в предыдущих главах, о линейности и дифференцируемости функций не делается никаких предположений, поэтому применение классических методов оптимизации (например, метода Лагранжа) для решения задачи (3)-(4) либо проблематично, либо просто невозможно.

Содержательно задача (3)-(4) может быть интерпретирована как проблема оптимального вложения некоторых ресурсов j, приводимых к единой размерности (например, денег) с помощью коэффициентов а_j в различные активы (инвестиционные проекты, предприятия и т. п.), характеризующиеся функциями прибыли f_j, т. е. такого распределения ограниченного объема ресурса (b), которое максимизирует суммарную прибыль. Представим ситуацию, когда она решается последовательно для каждого актива. Если на первом шаге принято решение о вложении в п-й актив х_п единиц, то на остальных шагах мы сможем распределить b-а_пх_п единиц ресурса. Абстрагируясь от соображений, на основе которых принималось решение на первом шаге (допустим, мы по каким-либо причинам не могли на него повлиять), будет вполне естественным поступить так, чтобы на оставшихся шагах распределение текущего объема ресурса произошло оптимально, что равнозначно решению задачи

(5)

при ограничениях

(6)

Очевидно, что максимальное значение (5) зависит от размера распределяемого остатка, и если оставшееся количество ресурса обозначить через , то величину (5) можно выразить как функцию от :

(7)

где индекс n - 1 указывает на оставшееся количество шагов. Тогда суммарный доход, получаемый как следствие решения, принятого на первом шаге, и оптимальных решений, принятых на остальных шагах, будет

(8)

Если бы имелась возможность влиять на х_п , то мы для получения максимальной прибыли должны были бы максимизировать по переменной х_п, т. е. найти и фактически решить задачу:

(9)

В результате мы получаем выражение для значения целевой функции задачи при оптимальном поэтапном процессе принятия решений о распределении ресурса. Оно в силу построения данного процесса равно глобальному оптимуму целевой функции

(10)

т. е. значению целевой функции при одномоментном распределении ресурса.

Если в выражении (5.9) заменить значения b на , и п на k , то его можно рассматривать как рекуррентную формулу, позволяющую последовательно вычислять оптимальные значения целевой функции при распределении объема ресурса за k шагов:

(11)

Значение переменной , при котором достигается рассматриваемый максимум, обозначим .

При k = 1 формула (5.11) принимает вид

(12)

т. е. допускает непосредственное вычисление функций и .

Воспользовавшись (12) как базой рекурсии, можно с помощью (11) последовательно вычислить и , . Положив на последнем шаге , в силу (9), найдем глобальный максимум функции (3), равный , и компоненту оптимального плана . Полученная компонента позволяет вычислить нераспределенный остаток на следующем шаге при оптимальном планировании: , и, в свою очередь, найти . В результате подобных вычислений последовательно будут найдены все компоненты оптимального плана.

Таким образом, динамическое программирование представляет собой целенаправленный перебор вариантов, который приводит к нахождению глобального максимума. Уравнение (11), выражающее оптимальное решение на k-м шаге через решения, принятые на предыдущих шагах, называется основным рекуррентным соотношением динамического программирования. В то же время следует заметить, что описанная схема решения при столь общей постановке задачи имеет чисто теоретическое значение, так как замыкает вычислительный процесс на построение функций , т. е. сводит исходную задачу (5.3)-(5.4) к другой весьма сложной проблеме. Однако при определенных условиях применение рекуррентных соотношений может оказаться весьма плодотворным. В первую очередь это относится к задачам, которые допускают табличное задание функций .

Задачи динамического программирования, допускающие табличное задание рекуррентных соотношений. Рассмотрим процесс решения модифицированного варианта задачи (3)-(4), в котором переменные x_j и параметры a_j, b могут принимать только целочисленные значения, а ограничение (4) имеет вид равенства. В рамках предложенной интерпретации о вложении средств в активы данные предпосылки вполне реалистичны и, более того, могут быть даже усилены требованием о кратности значений x_j, например, 1000 единицам.

Чтобы не усложнять обозначения, условимся операции целочисленной арифметики записывать стандартным образом, полагая, что промежуточные результаты подвергаются правильному округлению. Так, например, будем считать, что 12/5 = 2.

В соответствии с общей схемой вычислительного алгоритма на первом шаге мы должны построить функцию

Поскольку , x₁ принимает конечное число целых значений от 0 до b/a₁. Это позволяет, например, путем перебора значений найти функцию и задать ее в форме таблицы следующей структуры (табл. 1).

Последняя колонка табл. 1 содержит значение x_l, на котором достигается оптимальное решение первого шага. Его необходимо запоминать для того, чтобы к последнему шагу иметь значения всех компонент оптимального плана.

На следующем (втором) шаге можно приступить к вычислению функции , значения которой для каждого отдельно взятого находятся как

где значения

берутся из табл. 1. В результате вычислений формируется таблица значений , содержащая на одну колонку больше по сравнению с табл. 1, так как теперь необходимо запомнить оптимальные решения первого и второго шагов .

Таблица 1


0
1
…	…	…
B

На последующих шагах с номером осуществляются аналогичные действия, результатом которых становятся таблицы значений ,где (см. табл. 2).

Таблица 2

		…
0
1
…	…		…
b

На последнем п-ом шаге нет необходимости табулировать функцию , так как достаточно определить лишь . Одновременно определяется и оптимальное значение n-й компоненты оптимального плана . Далее, используя таблицу, сформированную на предыдущем шаге, определяем оптимальные значения остальных переменных:

и т. д. или, в общем виде,

(13)

Подчеркнем одно из преимуществ описанного метода с точки зрения его практической реализации в рамках программного обеспечения для ЭВМ: на каждом шаге алгоритма непосредственно используется только таблица, полученная на предыдущем шаге, т. е. нет необходимости сохранять ранее полученные таблицы. Последнее позволяет существенно экономить ресурсы компьютера.

Выигрыш, который дает применение рассмотренного алгоритма, может также быть оценен с помощью следующего простого примера. Сравним приблизительно по числу операций (состоящих, в основном, из вычислений целевой функции) описанный метод с прямым перебором допустимых планов задачи (3)-(4) при а₁=a₂=...а_n=1.

Количество допустимых планов такой задачи совпадает с количеством целочисленных решений уравнения

x_l+x₂+ ... +х_п =b,

т. е. равно числу сочетаний с повторениями из п элементов по b. Следовательно, при простом переборе число возможных вариантов составит

В случае применения метода динамического программирования для вычисления таблицы значений функции при фиксированном необходимо выполнить операций. Поэтому для заполнения одной таблицы необходимо проделать

операций, из чего получаем, что для вычисления всех функций , и потребуется

операций, что при больших п и b существенно меньше, чем в первом случае. Например, если п = 6 и b = 30, то непосредственный перебор потребует выполнения 324 632 операций, а метод динамического программирования — только 2511.

Задача о распределении средств между предприятиями.

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.

Рассмотрим схему решения задачи методом динамического программирования.

Задача: Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S₀= 5 у.е. Размеры вложения в каждое предприятие кратны 1 у.е. Средства х, выделенные i-тому предприятию (i = 1,2,3,4), приносят в конце года прибыль . Функция заданы таблично (таблица 1).

Таблица 1.

х
1	8	6	3	4
2	10	9	4	6
3	11	11	7	8
4	12	13	11	13
5	18	15	18	16

Принято считать, что :

1). Прибыль не зависит от вложения средств в другие предприятия;

2). Прибыль от каждого предприятия выражается в одних условных единицах;

3). Суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.

Определить какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.

Решение: Пусть - количество средств, выделенных i- тому предприятию. Суммарная прибыль . Переменные х удовлетворяют ограничениям . Математическая формулировка задачи: Найти переменные Х, удовлетворяющие системе ограничений и обращающие в максимум целевую функцию Z. Схема решения методом динамического программирования: Процесс решения распределения средств S₀= 5 у.е. можно рассматривать как четырех шаговый: номер шага соответствует номеру предприятия. - управление на 1 шаге, - управление на 2 шаге, - управление на 3 шаге, - управление на 4 шаге. S_кон = 0, т.к. все средства должны быть вложены в производство.

в общем виде . - состояния системы.

выражают количество средств оставшихся после i-ого шага. Это те средства, которые остается распределить между оставшимися 4-i предприятиями.

- условная оптимальная прибыль от i-ого предприятия, если между ними распределились оптимальным образом средства. Допустимые управления на i-том шаге удовлетворяют условию (либо i-тому предприятию ничего не выделяем, либо не больше того, что имеем к i-тому шагу).

Последовательно решим записанные уравнения, проводя условную оптимизацию каждого шага. Начинаем с 4 (четвертого) шага.

4 шаг. В таблице 1 прибыли монотонно возрастают, поэтому все средства, оставшиеся к 4 шагу, следует вложить в 4-е предприятие. При этом для возможных значений s₃ = 0,1,2,3,4,5 получим: и .

3 шаг. Делаем все предположения относительно остатка средств s₂ к 3 шагу(т.е. после выбора х₁ и х₂). s₂может принимать значения 0,1,2,3,4,5 (например, s₂= 0, если все средства отданы 1-му и 2-му предприятиям, s₂ = 5, если 1-е и 2-е предприятия ничего не получили, и т.д.). В зависимости от этого выбираем , находим и сравниваем для разных х₃ при фиксированном s₂ значения суммы . Для каждого s₂ наибольшее из этих значений есть - условная оптимальная прибыль, полученная при оптимальном распределении средств s₂ между 3-м и 4-м предприятиями. Оптимизация дана в таблице2 при i = 3. Для каждого значения s₂и помещены в графах 5 и 6 соответственно.

2 шаг Условная оптимизация проведена в таблице2 при i = 2. для всех возможных значений s₁ значения и находятся в столбцах 8 и 9 соответственно; первые слагаемые столбце 7 – значения , взяты из таблицы 1, а вторые слагаемые взяты из столбца 5 таблицы2 при .

1 шаг Условная оптимизация проведена в таблице2 при i = 1 для S₀= 5. Если х₁ = 0, то s₁ = 5, прибыль, полученная от четырех предприятий при условии, что s₁ = 5 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна ( взято из столбца 9 таблицы2 при s₁ = 5). Если х₁ = 1, то s₂=4. Суммарная прибыль при условии, что s₂= 4 ед. средств между оставшимися предприятиями будут распределены оптимально, равна ( взято из таблицы 1, а - из 9 столбца таблицы2). 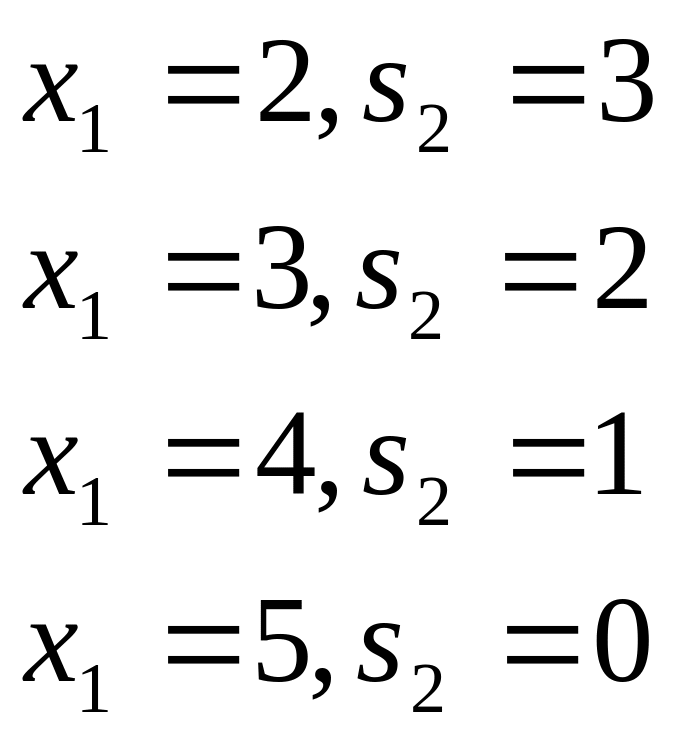Аналогично при

Сравнивая полученные числа, получим у.е.= при . Получим по таблице2 в столбце 9 находим . Далее находим , а по таблице2 в столбце 6 .Наконец, и , т.е.

Ответ: при

Таблица2

s_i-1	x_k	s_k	i=3			i=2			i=1
s_i-1	x_k	s_k
1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0
1	0 1	1 0	0+1=1 3+0=3	4	0	0+4=4 6+0=6	6	1	0+6=6 8+0=8	8	1
2	0 1 2	2 1 0	0+6=6 3+4=7 4+0=4	7	1	0+7=7 6+4=10 9+0=9	10	1	0+10=10 8+6=14 10+0=10	14	1
3	0 1 2 3	3 2 1 0	0+8=8 3+6=9 4+4=8 7+0=7	9	1	0+9=9 6+7=13 9+4=13 11+0=11	13	1 2	0+13=13 8+10=18 10+6=16 11+0=11	18	1
4	0 1 2 3 4	4 3 2 1 0	0+13=13 3+8=11 4+6=10 7+4=11 11+0=11	13	0	0+13=13 6+9=15 9+7=16 11+4=15 13+0=13	16	2	0+16=16 8+13=21 10+10=20 11+6=17 12+0=12	21	1
5	0 1 2 3 4 5	5 4 3 2 1 0	0+16=16 3+13=16 4+8=12 7+6=13 11+4=15 18+0=18	18	5	0+18=18 6+13=19 9+9=18 11+7=18 13+4=17 15+0=15	19	1	0+19=19 8+16=24 10+13=23 11+10=21 12+6=18 18+0=18	24	1

Практическое задание: Найти оптимальное распределение средств между n предприятиями при условии, что прибыль , полученная от каждого предприятия, является функцией от вложенных в него средств х. Вложения кратны Δх, а функции заданы таблично. S₀=5, n=4, Δх = 1.

х
1	0,2	1,0	2,1	0
2	0,9	1,1	2,5	2,0
3	1,0	1,3	2,9	2,5
4	1,2	1,4	3,9	3,0
5	2,0	1,8	4,9	4,0

Оформить таблицей, записать ответ

Задача о замене оборудования.

Оборудование эксплуатируется в течении 5 лет, после этого продается. В начале каждого года можно принять решение сохранить оборудование или заменить его новым. Стоимость нового оборудования р₀ = 4000руб. После t эксплуатации ( ) оборудование можно продать за (ликвидная стоимость). Затраты на содержание в течение года зависят от возраста t оборудования и равны . Определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минимальны.

Решение Делим управление на шаги по годам n = 5. Параметр состояния – возраст машины - - машина новая в начале первого года эксплуатации. Управление на каждом шаге зависит от двух переменных Х^с и Х^з.

Управления зависят от управления:

Показатель эффективности к-того шага:

Пусть - условные оптимальные затраты на эксплуатацию машины, начиная с к-го шага до конца, при условии, что к началу к-го шага машина имеет возраст t лет. Запишем для функции уравнения Беллмана:

Величина 4000*2^-(^t⁺¹⁾ – стоимость машины возраста t лет (по условию машина после 5 лет продается).

Из определения функций следует

Геометрическое решение задачи. На оси абсцисс откладывается номер шага к, на оси ординат – возраст t машины. Точка (к-1,t) на плоскости соответствует началу к-го года эксплуатации машины возраста t лет.

Состояние эксплуатации машины соответствует точке , конец - точкам .любая траектория переводящая точку s(k-1,t) из в , состоит из отрезков – шагов, соответствующих годам эксплуатации. Надо выбрать такую траекторию, при которой затраты на эксплуатацию машины окажутся минимальными.

рис.1

Над каждым отрезком, соединяющим точки (к-1,t) и (k,t+1), запишем соответствующие управлению Х^с затраты, найденные из 600(t+1), а над отрезком соединяющим точки (к-1,t) и (к,t) запишем затраты, соответствующие управлению Х^з, т.е. 4600-4000*2^-^t. Таким образом мы разметим все отрезки, соединяющие точки на графике, соответствующие переходам из любого состояния s_k_-1 в состояние s_k.

Проведем условную оптимизацию на размеченном графе состояний (рис.2).

4 шаг. Начальные состояния – точки (4;t), конечные (5;t). В состояниях (5;t) машина продается, условный оптимальный доход от продажи равен 4000*2^-^t, но поскольку целевая функция связана с затратами, то в кружках точек (5,t) поставим величину дохода со знаком минус.

Состояние (4,1). Из него можно попасть в состояние (5,2), затратив на эксплуатацию машины 1200 и выручив затем от продажи 1000, т.е. суммарные затраты равны 200, и в состояние (5,1) с затратами 2600-2000=600. Значит, если к последнему шагу система находилась в точке (4,1), то следует идти в точку (5,2) (укажем это направление двойной стрелкой), а неизбежные минимальные затраты, соответствующие этому переходу, равны 200 (поместим эту величину в кружке (4,1).

Состояние (4,2).Из него можно попасть в точку (5,3) с затратами 1800-500 = 1300 и в точку (5,1) с затратами 3600-2000=1600. Выбираем первое управление, отмечаем его двойной стрелкой, а проставляем в кружке точки (4,2).

Рассуждая таким образом для каждой точки предпоследнего шага, найдем для любого исхода 4 шага оптимальное управление на 5 шаге, отметим его на рис.2 двойной стрелкой. Далее планируем 4 шаг, анализируя каждое состояние, в котором может оказаться система в конце 3-го шага с учетом оптимального продолжения конца процесса. Например, если начало 4 шага соответствует состоянию (3,1), то при управлении Х^с система переходит в точку (4,2), затраты на этом шаге 1200, а суммарные затраты за два последних шага равны 1200+1300=2500. При управлении Х^з затраты за два шага равны 2600+200=2800. Выбираем минимальные затраты 2500,ставим их в кружок точки (3,1), а соответствующие управления на этом шаге выделены двойной стрелкой, ведущей из состояния (3,1), в состояние (4,2). Так поступаем для каждого состояния (3,t).

Продолжая условную оптимизацию 3, 2,и1 шагов получим на рис.2 следующую ситуацию: из каждой точки (состояния) выходит стрелка, указывающая, куда следует перемещаться на данном шаге, если система оказалась в этой точке, а в кружках записаны минимальные затраты на переход из этой точки в конечное состояние.

После проведения условной оптимизации получим в точке (0,0) минимальные затраты на эксплуатацию машины в течение 5 лет с последующей продажей: Z_min = 11900. далее строится оптимальную траекторию, перемещаясь из точки s₀(0,0) по двойным стрелкам в . Получаем набор точек: , который соответствует оптимальному управлению . Оптимальный режим эксплуатации состоит в том, чтобы заменить машину новой в начале 3-го года.

Таким образом, размеченный график (сеть) позволяет наглядно интерпретировать расчетную схему и решить задачу методом динамического программирования.

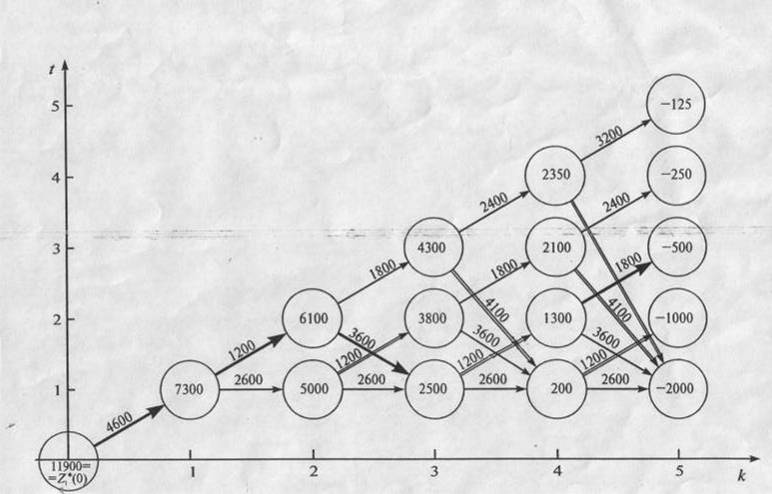
Практическая часть: Для задач 1), 2) составить математическую модель, записать уравнения Беллмана и решить графически следующие задачи на определение оптимальных сроков замены оборудования. Даны: первоначальная стоимость оборудования р₀, его ликвидная стоимость φ(t), стоимость содержания r(t) в течение года оборудования возраста t лет, n – срок эксплуатации, в конце которого оборудование продается. Критерий оптимальности – суммарные затраты на эксплуатацию оборудования в течение n лет с учетом первоначальной покупки и последующей продажи.

1). р₀ = 8000, φ(t) = р₀*2^-^t , r(t) = 0,1* р₀*(t+1), n = 5

2). Дополнительное задание: n = 5. Стоимость нового оборудования зависит от года покупки р_к = 5000 + 500(к-1), (к = 1, 2,…,5), φ(t) = р_к*2^-^t, r_k(t) = 0,1*р_к(t+1).

Алгоритмы в графах.

Граф определяется как пара (двойка) множеств — множество вершин W и множество ребер L: G = (W, L).

Вершины графа изображаются точками, ребра — линиями связи любой формы (граф — объект не геометрический, а топологический).

Количество вершин графа, т.е. мощность (количество элементов множества W, — это его порядок n: |W| = n.

Любой граф может быть однозначно задан с помощью матрицы смежности MS .

Свойства матрицы смежности:

— матрица квадратная порядка

— матрица бинарная (двоичная);

— на главной диагонали MS только нули (в графе не должно быть

петель);

— матрица симметрична относительно главной диагонали.

Мультиграфы, когда смежные вершины могут быть связаны несколькими ребрами (имеет смысл для отмеченных графов), и псевдографы, где есть петли и, возможно, расщепление ребер.

Вторая разновидность матричного представления графов — матрица инциденций MI: строки в Ml отображают ребра и вершины, с ними связанные (им инцидентные).

Свойства матрицы инциденций:

— в общем случае матрица прямоугольная;

— матрица бинарная (0, 1);

— в каждой строке матрицы Ml ровно 2 единицы, они указывают инцидентные вершины; в свою очередь, строки указывают ребра, инцидентные соответствующим вершинам.

Удаляя вершины (не все) и ребра из некоторого графа, получают подграф. А сам граф именуется надграфом. Если вершины не удаляются, получают остовный подграф.

Графы эквивалентны, если они, конечно, имеют одинаковый порядок и одинаковый характер связей — соответствующие вершины в обоих графах или связаны каким-то ребром или же не связаны вовсе.

Степень вершины графа — количество прилежащих ребер.

Если все вершины имеют одинаковую степень, граф — регулярный такой-то степени.

Теорема о сумме степеней всех вершин графа. В символической форме: ,т.е., сумма эта равна удвоенному количеству ребер.

Теорема о количестве вершин нечетной степени: количество таких вершин имеет значение четного числа.

Полный граф имеет максимально возможное количество ребер, обозначается К_n .

В двудольных графах допускаются связи только между вершинами разных долей.

Если в двудольном графе количество ребер максимально возможное, он — полный двудольный граф.

Маршрут в графе — это последовательность проходимых ребер и вершин.

Частный случай маршрута — путь, где повторение ребер не допускается. Маршруты и пути могут быть разомкнутые и замкнутые (циклы).

Длин а маршрут а (пути) — это количество проходимых ребер.

Граф без циклов — ациклический. В связном графе любые две вершины взаимно достижимы, т. е. существует хотя бы один маршрут из любой вершины в любую другую.

Дерево — это связный ациклический граф.

В корневом дереве одна из вершин специально выделяется и именуется корень. Остовное дерево — это остовный подграф, являющийся деревом.

Теорема о количестве маршрутов заданной длины: Количество маршрутов длины к из вершины w_i. в вершину w_j. определяется значением элемента i j к-й степени матрицы смежности, т.е. .

Теорема о количестве маршрутов доказывается по индукции (полная математическая индукция). На основе степеней матрицы смежности строится матриц а связности MSW. Это квадратная, порядка n, бинарная матрица, симметричная относительно главной диагонали.

Теорема о связности графа: Для связности графа, т.е. для взаимной достижимости любых его двух вершин, необходимо и достаточно, чтобы матрица связности MSW была полностью единичной.

Если граф несвязный, он распадается на компоненты связности.В случае, если компоненты связности — деревья, получается лес. Если к тому же это остовный подграф, то— остовный лес. Отдельные свойства связных графов — их эйлеровость и гамильтоновость («-ость» считаем допустимым элементом словообразования).

Граф эйлеров, если в нем существует замкнутый маршрут, проходящий через каждое ребро ровно 1 раз (т.е. фактически — это замкнутый путь). Говорят еще: эйлерова цепь, эйлеров цикл. Если все ребра проходятся по 1 разу, но путь-маршрут не замкнут, граф — полуэйлеров. Все прочие графы — неэйлеровы.

Гамильтоновость , полугамильтоновость , негамильтоновость графа определяются аналогично, но здесь речь идет о неповторяемости и однократной проходимости вершин, а не ребер.

Планарные графы

Планарный граф может быть изображен на плоскости без пересечения ребер . Такое изображение — карта графа. Карта связная, если планарный граф — связный.

Область карты графа — часть плоскости, ограниченная контуром из ребер. Степень области — количество ребер, составляющих границу области.

Теорема о сумме степеней всех областей планарного графа (может быть, даже и несвязного): , т.е. сумма эта равна удвоенному количеству ребер.

Теорем а Эйлер а для связных планарных графов: |W|—|L|+|R| = 2 т.е. количество вершин минус количество ребер плюс количество областей есть величина постоянная (константа Эйлера Е), имеющая значение 2

Теорема Эйлера справедлива и в отношении правильных выпуклых многогранников: |W|—|L|+|G| =E =2 здесь G — множество граней.

Необходимое и достаточное условие планарности графа сформулировано в теореме К. Куратовского, польского математика. Вводится операция элементарного стягивания — две смежные вершины сливаются, количество ребер при этом сокращается.

Теорема Куратовского утверждает: граф планарный тогда и только тогда, когда в процессе выполнения операций элементарного стягивания он не содержит подграфов вида К₅ и К_3,3 .

ми, разделяющими смежные области. Двойственный граф на рис.

Ориентированные графы (орграфы)

Можно отметить два существенных отличия орграфов от обычных графов :

— ориентация ребер, которые становятся дугами (дуга — «ребро со стрелкой»);

— наличие петель.

Как и обычные графы, орграфы однозначно описываются их матрицами смежности.

Связность орграфов бывает троякая:

— слабая;

— односторонняя:

— сильная.

Сильная связность означает взаимную достижимость любой пары вершин «в обе стороны», т. е. с учетом ориентации дуг и в прямом, и в обратном направлении.

Одностороння я связность соответствует взаимной достижимости, по крайней мере, в одну сторону для любой пары вершин. При этом нет сильной связности.

Слабая связность определяется как связность только на уровне неориентированного графа, получающегося из орграфа путем исключения петель и стрелок (дуги превращаются в ребра).

Задачи на графах

Задачи на графах (на графовых моделях) обычно очень сложно алгоритмизируются, а при решении требуют колоссальных вычислительных ресурсов (машинной памяти и машинного времени).

Все такие задачи можно условно разделить на две группы:

— маршруты, деревья и т.п.;

— задачи с мерой.

В первой группе:

— отыскание пути (маршрута) в лабиринте;

— проверка графа на эйлеровость;

— построение остовного дерева для связного графа;

— ориентация графа;

Алгоритмы для решения указанных выше задач существуют, и даже во множестве. Например, остовное дерево для связного графа строится с использованием «поедающего» алгоритма — каждое ребро рассматривается всего один раз. Оно оставляется («окрашивается») или удаляется. Удаляется, если с его участием образуется цикл. Практический смысл эта задача получает, например, когда речь идет о сети дорог (ребер), соединяющих населенные пункты (вершины). Наиболее экономичный вариант (в смысле стоимости дорог), очевидно, и соответствует остовному дереву — циклы вносят избыточность, поскольку остовное дерево уже связно. Конечно, здесь не учитываются затраты времени на дорожное сообщение (суммарная длина дорог и т.п.).

Практический смысл имеет и задача ориентации графа. Здесь имеется в виду, что получающийся орграф — сильно связный. Тогда обеспечивается взаимная достижимость для любой пары вершин, причем в обе стороны. Это может означать, что в некотором, например, городе можно организовать одностороннее дорожное движение (все виды транспорта двигаются в одном направлении; «встречной полосы» в принципе нет). Оказывается, однако, не любой граф поддается такой ориентации. Необходимое и достаточное условие для этого — каждое ребро должно входить хотя бы в один цикл.

Задачи второй группы решаются на помеченных графах.

Вот некоторые из таких задач:

— минимальная связка;

— кратчайший путь;

— задача почтальона;

— задача коммивояжера;

— максимальный поток в сети;

— поток с минимальной стоимостью;

— транспортная задача с минимальной стоимостью;

— транспортная задача с минимальным временем.

Задач а о минимально й связке (например, минимизируется общая длина дорог) предполагает рассмотрение множества остовных деревьев (задача 3 из первой группы).

Задача почтальона заключается в построении замкнутого («от почты до почты») маршрута минимальной длины, проходящего по каждому ребру не мене е одного раза. Похоже на попытку построения эйлерова цикла, но там прохождение по каждому ребру — однократное . Общий алгоритм решения задачи до сих пор не найден.

Задача коммивояжера (разъездного торговца), также до сих пор нерешенная (в общем случае), — построение замкнутого маршрута минимальной длины, проходящего через каждую вершину (посещаемый с целью торговли населенный пункт, город) не менее одного раза.

В задаче о максимальном потоке оптимизируется распределение входного потока элементов-объектов в вычислительной, транспортной или какой-либо другой сети. Дуги орграфа сети отмечаются двумя значениями — пропускной способности и реального потока. Второе значение не может быть больше первого.

Транспортные задачи являются классическими задачами линейного математического программирования. Алгоритмы их решения хорошо разработаны.

Основные понятия теории графов.

Общие понятия. Граф определяется как пара (двойка) множеств — множество вершин W и множество ребер L: G = (W, L).

Количество вершин графа, т.е. мощность (количество элементов множества W, — это его порядок n: |W| = n.

Любой граф может быть однозначно задан с помощью матрицы смежности MS .

Свойства матрицы смежности:

— матрица квадратная порядка

— матрица бинарная (двоичная);

— на главной диагонали MS только нули (в графе не должно быть

петель);

— матрица симметрична относительно главной диагонали.

Свойства матрицы инциденций:

— в общем случае матрица прямоугольная;

— матрица бинарная (0, 1);

Степень вершины графа — количество прилежащих ребер.

Если все вершины имеют одинаковую степень, граф — регулярный такой-то степени.

Теорема о количестве вершин нечетной степени: количество таких вершин имеет значение четного числа.

Полный граф имеет максимально возможное количество ребер, обозначается К_n .

В двудольных графах допускаются связи только между вершинами разных долей.

Если в двудольном графе количество ребер максимально возможное, он — полный двудольный граф.

Маршрут в графе — это последовательность проходимых ребер и вершин.

Длин а маршрут а (пути) — это количество проходимых ребер.

Дерево — это связный ациклический граф.

Планарные графы

ми, разделяющими смежные области. Двойственный граф на рис.

Ориентированные графы (орграфы)

Можно отметить два существенных отличия орграфов от обычных графов :

— ориентация ребер, которые становятся дугами (дуга — «ребро со стрелкой»);

— наличие петель.

Как и обычные графы, орграфы однозначно описываются их матрицами смежности.

Связность орграфов бывает троякая:

— слабая;

— односторонняя:

— сильная.

Задачи на графах

Все такие задачи можно условно разделить на две группы:

— маршруты, деревья и т.п.;

— задачи с мерой.

В первой группе:

— отыскание пути (маршрута) в лабиринте;

— проверка графа на эйлеровость;

— построение остовного дерева для связного графа;

— ориентация графа;

Задачи второй группы решаются на помеченных графах.

Вот некоторые из таких задач:

— минимальная связка;

— кратчайший путь;

— задача почтальона;

— задача коммивояжера;

— максимальный поток в сети;

— поток с минимальной стоимостью;

— транспортная задача с минимальной стоимостью;

— транспортная задача с минимальным временем.

Методы хранения графов в памяти ЭВМ.

Существуют различные способы представления графов.

Матрица инцидентности.

Это прямоугольная матрица размерности mхn, где n – количество вершин, а m – количество ребер. Значения элементов матрицы определяется следующим образом: если ребро x_i и вершина v_j инцидентны, то значение соответствующего элемента матрицы равно единице, в противном случае значение равно нулю. Для ориентированных графов матрица инцидентности строится по следующему принципу: значение элемента матрицы равно единице, если ребро x_i исходит из вершины v_j, равно 1, если ребро x_i заходит из вершины v_j, и равно 0 в противном случае.

Матрица смежности.

Это квадратная матрица размерности nxn, где n – количество вершин. Если вершины v_i и v_jсмежны, т.е. если существует ребро, их соединяющее, то соответствующий элемент матрицы равен единице, в противном случае он равен нулю. Правила построения данной матрицы для ориентированного графа не отличаются. Матрица смежности более компактна, чем матрица инцидентности. Следует заметить, что эта матрица также сильно разрежена, однако в случае неориентированного графа она является симметричной относительно главной диагонали, поэтому можно хранить не всю матрицу, а только половину (треугольную матрицу).

Список смежности (инцидентности).

Представляет собой структуру данных, которая для каждой вершины графа хранит список смежных с ней вершин. Список представляет собой массив указателей, i-ый элемент которого содержит указатель на список вершин, смежных с i-ой вершиной.

Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.

Список списков.

Представляет собой древовидную структуру данных, в которой одна ветвь содержит списки вершин, смежных для каждой из вершин графа, а вторая ветвь указывает на очередную вершину гарфа. Такой способ преставления графа является наиболее оптимальным.

Для реализации графа в виде списка инцидентности можно использовать следующий тип:

Type List = ^S;

S = record;

inf: Byte;

next: List;

end;

тогда граф задается следующим образом:

Var Gr: array [1…n] of List;

Используют также процедуру обхода графа. Это вспомогательный алгоритм, который позволяет просмотреть все вершины графа, проанализировать все информационные поля.

Граф можно определить с помощью списка списков следующим образом:

Type List = ^TList;

TList = record;

inf: Byte;

next: List;

end;

Graph = ^T Graph;

T Graph = record;

inf: Byte;

smeg: List;

next: Graph;

end;

При обходе графа в ширину выбирают произвольную вершину и просматривают сразу все смежные с ней. Вместо стека используется очередь. Алгоритм обхода в ширину очень удобен при нахождении кратчайшего пути в графе.

Методы нахождения кратчайших путей в графе.

Путь минимальной длины между вершинами v_i и v_j при этом называется кратчайшим путем в графе. В невзвешенном графе G длиной пути между вершинами v_i и v_j называется количество ребер в пути. Если пути нет вообще, то расстояние считается равным бесконечности.

Длиной пути между двумя вершинами во взвешенном графе G называется сумма весов ребер, составляющих этот путь. В отличие от невзвешенного графа, наличие ребра между двумя вершинами не гарантирует, что кратчайший путь между ними состоит из этого ребра. Зачастую суммарный вес пути, состоящего из двух, трех и более ребер, может оказаться меньше веса одного ребра, поэтому даже для полного графа задача поиска кратчайшего пути имеет смысл.

Пусть задан граф G, каждой дуге которого поставлено в соответствие неотрицательное

число l_i_,_j, называемое длиной. Выделим две вершины S и t. Задача состоит в том, чтобы найти путь минимальной длины между ними. Если в графе имеются кратные дуги (соединяющие одинаковые начало и конец), достаточно оставить одну - с наименьшей длиной, а остальные отбросить. Таким образом, достаточно рассматривать задачу о кратчайшем пути для простого графа, в котором дуги

определяются упорядоченными парами вершин (v₁,v₂). Тогда естественно путь L, идущий из вершины S в вершину t, задавать в виде упорядоченного набора вершин, через которые проходит данный путь: L=(S = v_0,,v₁,v₂,..., v_n_-1, v_n = t)

Метод Минти.

Метод Минти решения задачи о кратчайшем пути в сети представляет собой итеративный процесс, в ходе которого строится путь L=(S = v_0,,v₁,v₂,..., v_n_-1, v_n = t).

Он пригоден для определения кратчайшего пути как во взвешенном, так и в невзвешенном графе. На предварительном (нулевом) этапе алгоритма:

1)Формируется массив значений так называемых модифицированных длин, которые перед началом первой итерации полагаются равными l_i_,_j ≥0;

2)Осуществляется отметка вершины S = v₀ числом m₁=0.

Стандартная итерация включает следующие этапы:

1.Отметка вершин сети.

Обозначим множество вершин сети, отмеченных на предыдущих итерациях

как множество М (на первой итерации М= { v₀}). Для каждой вершины v_i из множества М пишутся дуги, соединяющие ее с еще не помеченными вершинами - потомками v_j, модифицированная длина которых c_i_,_j =0. Найденные таким способом вершины v_j помечаются числом m_j=i, указывающим на «родителя». В том случае, когда сразу несколько дуг, имеющих c_i_,_j =0, заканчиваются в одной и той же вершине v_j, значение для ее пометки i выбирается произвольно. Если среди вновь помеченных вершин окажется вершина t, то, значит, найден искомый путь

L=(S = m₁,m₂,m₃,..., m_n_-1, m_n = t), на чем алгоритм завершается. В случае, если вершины t нет среди помеченных, и одновременно нельзя отметить ни одной новой вершины, то переходим к этапу 2.

2.Преобразование значений модифицированных длин дуг. Для каждой вершины v_i из множества M ищутся дуги, соединяющие ее с еще не помеченным вершинами v_j, и находятся оценки .

Далее модифицированные длины всех дуг, которые соединяют отмеченные вершины v_i из множества М c непомеченными вершинами v_j, уменьшаются на величину

в результате чего кратчайшие неиспользованные дуги получают нулевую модифицированную длину. Затем происходит переход к следующей итерации.

Образец решения задачи.

Пусть дан граф G. Определим кратчайший путь из вершины 1 в вершину 6.

2 2

3 8

На предварительном этапе вершина 1 отмечается числом m₁ =0, а модифицированные длины совпадают с заданными длинами дуг.

Итерация 1. Так как из вершины 1 не выходят дуги нулевой длины, дальнейшая отмел невозможна. Переходим к этапу 2. Смежными с вершиной 1 являются вершины 2 и 3. Для них определяем

и вычитаем ее из c₁₂ и c₁₃. После преобразования имеем c₁₂=0, c₁₃=l.

0 2

1 8

Итерация 2.

Помечаем вершину 2 m₂ =1. Дальнейшая пометка невозможна, поэтому переходим к этапу

2. Смежными с помеченными вершинами 1 и 2 являются вершины 3,4,5. Определяем

и после соответствующего преобразования имеем c₁₃=0, c₂₃=0, c₂₄=1,c₂₅=9.

1 9

0 2

0 8

Итерация 3.

В вершину 3 ведут дуги нулевой длины как из вершины 1, так и из вершины 2. Поскольку выбор здесь может быть произвольным, пометим вершину 3 числом

m₃ =1. Дальнейшая пометка невозможна, поэтому переходим к этапу 2. Смежными с ранее отмеченными вершинами являются

и после преобразования имеем c₂₄=0, c₂₅=8, c₃₄=5, c₃₅=3.

0 8

(2)1 5

Итерация 4.

Помечаем вершину 4 m₄ =2. Дальнейшая пометка невозможна, поэтому переходим к этапу 2. Смежными с ранее помеченными вершинами являются вершины 5,6. Определяем

и после преобразования имеем c₂₅=5, c₃₅=0, c₄₅=0, c₄₆=5.

0 2

0 5

(2)1 5

Итерация 5. В вершину 5 ведут дуги нулевой длины как из вершиныЗ, так и из вершины 4. Руководствуясь теми же соображениями, что и на итерации.З, пометим вершину 5 числом m₅=3

0 0

0 3

(2)1 5 2

Дальнейшая пометка невозможна, поэтому переходим к этапу 2. Смежной с ранее отмеченными вершинами является вершина 6. Отсюда определяем

и после преобразования имеем c₄₆=3, c₅₆=0.

Итерация 6. В вершину 6 ведет дуга нулевой длины из вершины 5, поэтому помечаем ее числом m₆= 5. Поскольку мы отметили конечную вершину маршрута, то алгоритм завершен и мы можем, используя значения отметок для родителей, выписать искомый кратчайший путь (1,3,5,6).

1 3(4)

2 2

0 5

L_min=9 ед.

(2)1 6 2

Следует также добавить, что если бы наш выбор на итерациях 3 и 5 был иным, то мы получили бы альтернативные, пути той же длины (1,2,3,5,6), т.е. рассмотренная задача имеет несколько решений.

Алгоритм Форда-Фалкерсона.

Введём некоторые обозначения:

Пропускная способность дуги – некоторое положительное b_ij число, поставленное в соответствие дуге (v_i, v_j).

Поток из источника S в сток t – множество неотрицательных чисел, поставленных в соответствие некоторой дуге сети, если числа удовлетворяют следующим линейным ограничениям:

-v, если v_j=s;

∑x_ij - ∑x_jk = 0, если v_j≠ s, v_j≠ t;

_{i
k}

v, если v_j = t;

v ≥ 0; 0≤x_ij≤b_ij для всех i, j

Здесь:

а) x_ij – поток между вершинами v_i и v_j

b) x_kj - поток между вершинами v_i и v_k

c) первую сумму берут по дугам, ведущим в вершину v_j,

d)вторую сумму берут по дугам, ведущим из вершину v_j

Неотрицательное число v называют величиной потока. Число x_ij называют потоком по дуге (v_i, v_j) или дуговым потоком. Ограничения выражают тот факт, что в каждую вершину (кроме источника и стока) приходит столько потока, сколько из него уходит (условие сохранения потока), и что поток x_ij по дуге ограничен пропускной способностью дуги b_ij.

Обозначим через F_st множество неотрицательных чисел x_ij,удовлетворяющих поставленным ограничениям. Будем называть путь из S в t увеличивающим поток F_st, если x_ij<b_ij на всех прямых дугах и x_ji>0 на всех обратных дугах этого пути. Поток F_stмаксимален тогда и только тогда, когда не существует пути, увеличивающего поток F_st. Величина максимального потока в любой сети принимает, безусловно, единственное значение. Ну может существовать несколько различных максимальных потоков F_st, имеющих одинаковую величину.

Пусть задана ориентированная сеть с одним источником S и одним стоком t и пусть дуги (v_i, v_j) имеют ограниченную пропускную способность. Задача о максимальном потоке заключается в поиске таких потоков по дугам, что результирующий поток, протекающий из источника S в сток t, является максимальным. Задача о максимальном потоке может быть сформулирована как задача линейного программирования, и поэтому может быть решена симплекс – методом. Однако для её решения можно применить более эффективный метод – метод расстановки пометок (метод разработан Фордом и Фалкерсоном).

Алгоритм начинает работу с некоторого допустимого решения, вершины рассматривает как промежуточные пункты передачи потока, а дуги – пометки и увеличивающие (аугментальные) пути потока. Пометку вершину используют для указания как величины потока, так и источника потока, вызывающего изменение текущего потока по дуге, соединяющий этот источник с рассматриваемой вершиной. Если q_i единиц потока посылают из вершины v_i в вершину v_j и это вызывает увеличение потока по этой дуге , то будем говорить, что вершина v_jпомечена из вершины v_i символом (+ q_i); в данном случае вершине v_j приписывают пометку [+q_i; v_i]. Если посылка q_i единиц потока вызывает уменьшение потока по дуге, то будем говорить, что вершина v_j помечена из вершины v_i символом(-q_j). В таком случае вершине приписывают пометку [-q_i;v_i].

Текущий поток из вершины v_i в вершину v_j увеличивается, когда q_j единиц дополнительного потока посылается в вершину v_j по ориентированной дуге (v_i, v_j) в направлении, совпадающем с её ориентацией. В таком случае дугу называют прямой. Если q_i единиц дополнительного потока посылаются в вершину v_j по ориентированной дуге (v_j; v_i), т.е. в направлении, противоположном её ориентации, то текущий поток из v_j в v_i уменьшается, а дугу (v_j; v_i) называют обратной. Вершина v_j может быть помечена из вершины v_i только после того, как вершине v_i приписана пометка. Если вершина v_j помечена из вершины v_iи дуга (v_i, v_j) прямая, тот поток по данной дуге увеличивается, и величина, соответствующая оставшейся неиспользованной пропускной способности дуги, должна быть нужным образом скорректирована. Если некоторой вершине приписывают пометку и при этом используют прямую ветвь, то она может иметь только остаточную пропускную способность.

Увеличивающий (аугментальный) путь потока из S в t определяют как связанную последовательность прямых и обратных дуг, по которым из S в t можно послать несколько единиц потока. Поток по каждой прямой дуге увеличивается, при этом не превышает её пропускной способности, а поток по каждой обратной дуге уменьшается, оставаясь при этом неотрицательным. Аугментальный путь потока используют для выбора такого способа изменения потока, при котором поток в узле t увеличивается, и для каждого внутреннего узла сети при этом не будет нарушено условие сохранения потока.

Как конкретно можно увеличить поток на q_j единиц? Предположим, что дуге (v_i, v_j) уже приписан поток x_ij ≥ 0; причем x_ij≤ b_ij - пропускная способность дуги (v_i, v_j). Величина q_i не может превосходить остаточной пропускной способности b_ij – x_ij. Но из вершины v_i не всегда можно получить b_ij – x_ij единиц потока. Отметим, что в вершину v_j можно послать столько единиц потока, сколько их добавляется в вершину v_i , т. е. самое большое q_i. Следовательно, поток по прямой дуге (v_i, v_j) можно увеличить на q_i = min[q_i, x_ij-b_ij]. Аналогично получается для вершины, если дуга (v_j, v_i) является обратной. Уменьшение потока по дуге (v_j, v_i) возможно только в том случае, когда x_ji≥ 0. поток может быть уменьшен самое большее на число единиц потока, которые можно взять из вершины v_i т. е. на q_i. Следовательно, поток по обратной дуге (v_j, v_i) может быть уменьшен на q_j=min[q_i; x_ji].

В начале работы алгоритма источнику приписывают пометку [∞;-], указывающую на то, что из данной вершины может вытекать поток бесконечно большой величины. Далее мы ищем аугментальный путь потока от источника к стоку, проходящему через помеченные вершины. Все вершины (за исключением источника) в начальный момент не помечены. Пытаясь достичь стока, мы проходим, выбирая дуги с наибольшими пропускными способностями, по прямым и обратным дугам и последовательно помечаем принадлежащие им вершины. Возможны два случая:

1. стоку приписывают пометку [+q;k], k-номер вершины, связанный со стоком. В этом случае аугментальный путь потока найден и поток по каждой дуге этого пути может быть увеличен или уменьшен на q_t. После изменения дуговых потоков текущие пометки стирают и всю описанную процедуру повторяют заново.

2. сток t не может быть помечен. Этот означает, что аугментальный путь потока не может быть найден. Следовательно, построенные дуговые потоки образуют оптимальное решение (максимальный поток).

Задача.

Найти максимальное количество информации, которое может быть передано из источника S в сток t по сети, представленной на рисунке 1. Пропускные способности дуг b_ij отмечены.

4 рис.1 Исходные данные для задачи о максимальном

потоке (о максимальном 2 количества информации).

2 3

Итерация 1.

Каждой дуге (v_i, v_j) приписывают пометку [ x_ij; b_ij], где x_ij – текущий дуговой поток, b_ij_–пропускная способность дуги. приписываем вершине S пометку [∞;-]. Из источника S максимальный поток идет в вершину 2; вершине 2 приписываем пометку [+3;S], так как q₂=min[q_s;b_s₂]=min[∞;3]=3. из вершины 2 максимального пропускная способность принадлежит дуге (2,t) ведущей в сток t. Приписываем стоку пометку [2;2], так как q_t=min[q₂;b₂_t] = min[3;2]=2. изменение дуговых потоков возможно на 2 единицы: x_s₂=2, x₂_t=2. Дуги получают пометки, показанные на рисунке 2.

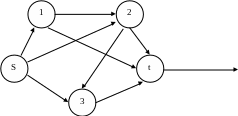[0,4] рис.2 первая итерация

[0,3] 3

[2,2] 0

[0,2] [2,3]

[0,1]

поток равен 2 ед.

[0,2] 2

[0,1]

Итерация 2.

Теперь просматриваем остаточные пропускные способности b_ij-x_ij (выделены голубым цветом или жирным шрифтом на рис.1). источнику S приписываем пометку [∞;-]. Из источника S предпочтительнее двигаться в вершину 1, вершине 1 приписываем пометку [2;S]. Из вершины 1 идем в вершину 2; вершине 2 приписываем пометку [2;1], так как q₂=min[q₁;b₁₂-x₁₂]=2. из вершины 2 идем в вершину 3. для третьей вершины q₃=min[q₂;b₂₃-x_23]=min[2;1]=1; вершине 3 приписываем пометку [1;2].из вершины 3 идем в сток. Стоку приписываем пометку [1;3]. Минимальное изменение дуговых потоков равно 1, т. е. изменение дуговых потоков будет x₃₁=1, x₁₂=1, x₂₃=1, x₃₁=1. максимальный поток равен 2+1=3 ед. дуги получают следующие пометки, показанные на рисунке 3.

[0,4] рис.3 вторая итерация

[0,3]3

[2,2] 0

[1, 2] [2,3]

[1,1]

Поток равен 3 ед.

[0,1]

[1,2] 1

Итерация 3.

Приписываем вершине S пометку [∞;-]. Из вершины S движемся в вершину 1:q₁=max[q_s;b_s₁-x_s₁]=min[∞;1]=+1. вершине 1 приписываем пометку [+1;S]. Из вершины 1 идем в сток t: q_t=min[q₁;b₁_t-x₁_t]=min[1;3]=1. стоку t приписываем пометку [1;1]. Изменение дуговых потоков для x_s₁ равно 1, для x₁_t равно 1; изменяются только значения потоков на дугах (S;1) и91;t). Полные потоки станут x_s₁=2; x₁_t=1. дуги получают пометки, показанные на рисунке 4. максимальный поток станет равным 3+1=4 ед.

[1,4] рис.4 третья итерация

[0,3]2

[2,2] 0

[2, 2] [2,3]

[1,1]

Поток равен 4 ед.

[0,1]

[1,2] 1

Итерация 4.

Приписываем вершине S пометку [∞;-]. Из вершины S направляемся в вершину 2:q₂=min[q_s;b_s₂-x_s₂]=min[∞;1]=+1; вершине 2 приписываем пометку [1;S]. из вершины 2 мы можем попасть в сток t, только пройдя по обратной дуге в вершину 1, а затем в сток t. Определим пометку для вершины 1 в данном случае: q₁=min[q₂,x₁₂]=min[1;4]=+1, т.е. вершине 1 приписываем пометку [1;2]. Для вершины t:q_t=min[q₁;u_1,_t-x₁_t]=min[1;1]=+1; вершине t приписываем пометку [1;1]. Изменение дуговых потоков для x_s₂, x₁₂, x₁_t равно 1. потоки по этим дугам будут соответственно x_s₂=2, x₁₂=0, x₁_t=2; максимальный поток из S в t равен 4+1=5 ед. Дуги получают пометки [изменяются пометки только на дугах (S,2); (1,2) и (1, t)], показанные на рисунке 5.

[0,4] рис.5 Четвертая итерация

[2,3]1

[2,2] 0

[2, 2] [3,3]

[1,1]

Поток равен 5 ед.

[0,1]

[1,2] 1

Итерация 5.

Приписываем вершине S пометку [∞;-1]. Из вершины S мы можем попасть только в вершину 3. для вершины 3:q₃=min[q_s;b_s₃-x_s₃]=min[∞,1]=+1. сток t получает пометку [1,3]. Изменение дуговых потоков для x_s₃ и x₃_t равно 1; соответственно потоки x_s₃=1, x₃_t=2. (на второй итерации было x₃_t=1). Максимальный поток равен 5+1=6 ед. дуги получают пометки, показанные на рис. 6.

[0,4] рис.6 пятая итерация

(оптимальное

[2,3] 1 решение)

[2,2] 0

[2,2] [3,3]

[1,1]

поток равен 6 ед.

[2,2] 0

[1,1]

Итерация 6.

Приписываем вершине S пометку [∞,-]. Аугментальный поток не может быть найден, т.е. построенные дуговые потоки образуют оптимальное решение. Максимальный поток (максимальное количество информации) из источника S в сток t равен 6ед. 2ед. потока идут из источника S через вершину 1 в сток t; 1ед. потока идет из источника S через вершину 3 в сток t; 3ед. потока идут из источника S в вершину 2, затем 2ед. потока поступают из вершины 2 в сток t, а 1ед. потока поступает в сток t через вершину 3. через дугу (1,2) информация не идет.

Образец решения задачи с использованием матриц.

Найти максимальный поток в сети.

Допусти S=v₁; t=v₆

(3)

(1) (2)

1 (3) 0

(1)

(6)

(5)

(3)

Алгоритм построения максимального потока.

Построить матрицу пропускных способностей сети B.
Построить некоторый начальный поток X₀.
Организовать процедуру составления подмножества А вершин, достижимых из истока S по ненасыщенным ребрам. Если в этом потоке сток не попадет в подмножество А, то построенный поток максимальный и задача решена. Если сток попал в это подмножество, то перейти к пункту 3.
Выделить путь из истока в сток, состоящий из ненасыщенных ребер (дуг), и построить новый поток, увеличив поток по этим ребрам на величину ∆=min[b_ij-x_ij], причем минимум берется по выбранным ненасыщенными ребрам. Перейти к пункту 2.

Решение.

1. Построить матрицу пропускных способностей:

B =

2. Построить матрицу начального потока:

X₀=

3. Построить матрицу остаточных пропускных способностей:

B – X =

Если ребро насыщено, тот соответствующий элемент матрицы остаточной пропускных способностей B – X равен нулю. Если ребро не насыщено, то элементы матрицы ненулевые.

4. Составить список вершин А от истока v₁ по ненулевым элементам и прямым дугам: выписать соответствующие номера вершин. Вершины, попавшие в список ранее, в него больше не включаются. Путь будет не насыщенным если в список попал сток. Если сток не попадет, то все ребра насыщены, и поток увеличить нельзя. Имеем: (1,2); (2,3); (3,4); (4,5);(5,6); A=(1,2,3,4,5,6)

получаем ненасыщенный путь 1-2-3-4-5-6. поток по этому ненасыщенному пути можно увеличить на величину минимальной остаточной пропускной способности

min{b_ij – x_ij}=min{2,1,1,1,2}=1

5. Составим матрицу потока X₁, увеличив соответствующие элементы (ребра, вошедшие в ненасыщенный путь) X₀ на величину 1:

X₁ =

(3)

2+1

(1) (2)

1 (3) 0+1

(1)

1+1

4+1

3+1

(6)

(5)

(3)

6. Построим матрицу остаточной пропускной способности:

B – X₁ =

7. Составим список вершин от истока 1 по ненулевым элементам и прямым дугам: выписываем номера вершин. Вершины, попавшие в список ранее в него больше не включаются. Путь будет ненасыщенным, если в список попал сток. Если сток не попадет, то все ребра насыщены, и поток увеличить нельзя. Имеем:

(1,2);(5,5) A=(1,2,3,4,5,6)

Получаем ненасыщенный путь 1-2. в данной цепочке отсутствует сток, поэтому все ребра насыщены, и поток более увеличит нельзя.

Максимальная величина потока

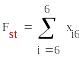
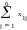
= 0 + 1 + 5 + 0 + 0 + 0=6 = = 0 + 0 + 0 + 2 + 4 + 0 = 6

Методы нахождения максимального потока в графе.

Введём некоторые обозначения:

Пропускная способность дуги – некоторое положительное b_ij число, поставленное в соответствие дуге (v_i, v_j).

-v, если v_j=s;

∑x_ij - ∑x_jk = 0, если v_j≠ s, v_j≠ t;

_{i
k}

v, если v_j = t;

v ≥ 0; 0≤x_ij≤b_ij для всех i, j

Здесь:

а) x_ij – поток между вершинами v_i и v_j

b) x_kj - поток между вершинами v_i и v_k

c) первую сумму берут по дугам, ведущим в вершину v_j,

d)вторую сумму берут по дугам, ведущим из вершину v_j

Задача.

4 рис.1 Исходные данные для задачи о максимальном

потоке (о максимальном 2 количества информации).

2 3

Итерация 1.

[0,4] рис.2 первая итерация

[0,3] 3

[2,2] 0

[0,2] [2,3]

[0,1]

поток равен 2 ед.

[0,2] 2

[0,1]

Итерация 2.

[0,4] рис.3 вторая итерация

[0,3]3

[2,2] 0

[1, 2] [2,3]

[1,1]

Поток равен 3 ед.

[0,1]

[1,2] 1

Итерация 3.

[1,4] рис.4 третья итерация

[0,3]2

[2,2] 0

[2, 2] [2,3]

[1,1]

Поток равен 4 ед.

[0,1]

[1,2] 1

Итерация 4.

[0,4] рис.5 Четвертая итерация

[2,3]1

[2,2] 0

[2, 2] [3,3]

[1,1]

Поток равен 5 ед.

[0,1]

[1,2] 1

Итерация 5.

[0,4] рис.6 пятая итерация

(оптимальное

[2,3] 1 решение)

[2,2] 0

[2,2] [3,3]

[1,1]

поток равен 6 ед.

[2,2] 0

[1,1]

Итерация 6.

Образец решения задачи с использованием матриц.

Найти максимальный поток в сети.

Допусти S=v₁; t=v₆

(3)

(1) (2)

1 (3) 0

(1)

(6)

(5)

(3)

Алгоритм построения максимального потока.

Построить матрицу пропускных способностей сети B.
Построить некоторый начальный поток X₀.
Организовать процедуру составления подмножества А вершин, достижимых из истока S по ненасыщенным ребрам. Если в этом потоке сток не попадет в подмножество А, то построенный поток максимальный и задача решена. Если сток попал в это подмножество, то перейти к пункту 3.
Выделить путь из истока в сток, состоящий из ненасыщенных ребер (дуг), и построить новый поток, увеличив поток по этим ребрам на величину ∆=min[b_ij-x_ij], причем минимум берется по выбранным ненасыщенными ребрам. Перейти к пункту 2.

Решение.

1. Построить матрицу пропускных способностей:

B =

2. Построить матрицу начального потока:

X₀=

3. Построить матрицу остаточных пропускных способностей:

B – X =

min{b_ij – x_ij}=min{2,1,1,1,2}=1

X₁ =

(3)

2+1

(1) (2)

1 (3) 0+1

(1)

1+1

4+1

3+1

(6)

(5)

(3)

6. Построим матрицу остаточной пропускной способности:

B – X₁ =

(1,2);(5,5) A=(1,2,3,4,5,6)

Максимальная величина потока

= 0 + 1 + 5 + 0 + 0 + 0=6 = = 0 + 0 + 0 + 2 + 4 + 0 = 6

Задачи в условиях неопределенности.

К этому разделу относятся задачи, следующих тем: Системы массового обслуживания, Имитационное моделирование, Прогнозирование, Теория игр, Теория принятия решений.

Теория систем массового обслуживания (СМО) восходит к работам А.К.Эрланга по исследованию причин неэффективности телефонных станций. Примерами СМО могут служить: телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, магазины, парикмахерские и т.п. Теория массового обслуживания – раздел исследования операций, который рассматривает разнообразные процессы в экономике, а также в телефонной связи, здравоохранении и других областях массового обслуживания, т.е. удовлетворения каких-то запросов, заказов. Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания. В качестве «каналов» могут фигурировать: линии связи, рабочие точки, приборы, железнодорожные пути, лифты, автомашины и т.д.

Имитационное моделирование – это процесс конструирования на ЭВМ модели сложной реальной системы, функционирующей во времени, и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии, обеспечивающие функционирование данной системы.

Имитационное моделирование предполагает два этапа: конструирование модели на и ЭВМ проведение экспериментов с этой моделью. Каждый из этих этапов предусматривает использование собственных методов. На первом этапе важно грамотно провести информационное обследование, разработку всех видов документации и их реализацию. Второй этап должен предполагать использование методов планирования эксперимента с учетом особенностей машинной имитации.

Научное познание и использование законов развития общества тесно связаны с прогнозами. Прогноз — научно обоснованное суждение о возможных состояниях объекта в будущем, альтернативных путях и сроках их осуществления.

Во многих областях человеческой деятельности часто встречается проблема принятия управленческих решений в условиях неопределенности. При этом неопределенность может быть связана как с сознательными действиями противниками, так и с другими факторами, влияющими на эффективность решения. Ситуация, в которых эффективность принимаемою одной стороной решения зависит от действий другой стороны называется конфликтными. Математическая модель конфликтной ситуации называется игрой. Конфликт не обязательно предполагает наличие антагонистических противоречий сторон, но всегда связан с определенного рода разногласиями.

Конфликтная ситуация будет антагонистической, если увеличение выигрыша одной из сторон на некоторую величину приведет к уменьшению выигрыша другой стороны на такую же величину и наоборот.

Выработкой рекомендаций по рациональному образу действий участников многократно повторяющегося конфликта занимается математическая теория конфликтных ситуаций – теория игр. Возникновение ее относится к 1944г., когда вышла в свет монография Дж. фон Неймана и О. Моргенштерна “Теория игр и экономическое поведение”.

В настоящее время теория игр бурно развивается. В последние годы помимо теории антагонистических, неантагонистических (кооперативных), конечных, бесконечных, позиционных и дифференциальных игр, начала развиваться теория рефлексивных игр. Рефлексивные игры изучают ситуации с учетом мысленного воспроизведения возможного образа действий и поведения противника. Дифференциальные игры изучают задачи преследования управляемого объекта другим управляемым объектом с учетом динамики их поведения; поведение объектов описывается дифференциальными уравнениями.

Игра представляет математическую модель реальной конфликтной ситуации, анализ которой ведется по определенным правилам.

В общем случае правилами игры устанавливается последовательность ходов, объем информации каждой стороны о поведении другой и результат (исход) игры. Правила определяют также конец игры, когда некоторая возможная последовательность выборов уже сделана, и больше ходов делать не разрешается.

В зависимости от числа участников игры подразделяются на парные и множественные. В парной игре число участников равно 2, в множественной – более 2^х. Участники множественной игры могут образовать коалиции (игры называют коалиционными). Множественная игра обращается в парную, если ее участники образуют 2 постепенные коалиции.

Рассмотрим еше один аспект классификации математических методов и моделей — элементы теории принятия решений.

Классификация решений

Будем говорить о принятии решений при управлении; опираясь на интуитивное понятие решения, как способа устранения проблемной ситуации.

Проблемная ситуация предполагает наличие:

• цели;

• ресурсов;

• альтернатив (способов действий);

• свойств окружающей среды.

Проблемная ситуация предполагает неудовлетворенность лица, принимающего решения («целеустремленное состояние»), и необходимость действий для устранения проблемы. Это может быть:

• снятие проблемной ситуации, т. е. такое изменение целей,

при котором неудовлетворенность исчезает;

• разрешение — изменение свойств окружающей среды или

ресурсов;

• решение ситуации, т. е. выбор альтернатив, которые позволяют

достичь данных целей при данных ресурсах.

Системы массового обслуживания.

СМО могут быть одноканальными или многоканальными.

Многоканальная система массового обслуживания – система, которой поступившее требование может быть обслужено одним из нескольких каналов.

Задачи массового обслуживания – класс задач исследования операций, заключающихся в нахождении оптимальных параметров системам массового обслуживания.

Неопределенность в системе – ситуация, когда отсутствует полностью или частично информация о возможных состояниях системы и внешней среды. Иначе говоря, когда в системе происходят те или иные непредсказуемые события. Это неизбежный атрибут больших (сложных) систем; чем сложнее система, тем большее значение приобретает фактор неопределенности в ее поведении (развитии).

Канал обслуживания (устройство, пункт, станция обслуживания) – понятие теории массового обслуживания, означающее устройство или средство, способное в данный момент времени обслуживать лишь одно требование. Пропускная способность канала – один из определяющих параметров при решении задач массового обслуживания. Другой его важнейшей характеристикой является среднее время обслуживания одной заявки.

Поток требований (заявок) – в теории массового обслуживания – последовательность требований или заявок, поступающих на пункт обслуживания (канал, станцию, прибор и т.д.)

Очередь – в теории массового обслуживания – последовательность требований или заявок которые, заставая систему обслуживания занятой, не выбывают, а ожидают ее освобождения (затем они обслуживаются в том или ином порядке). Очередью можно назвать также совокупность ожидающих (простаивающих) каналов или средств обслуживания.

Дисциплина обслуживания (в теории СМО) – совокупность правил, пользуясь которыми из очереди выбирают требования для обслуживания.

Каждая СМО предназначена для обслуживания (выполнения) какого-то потока заявок (требований), поступающих на СМО в какие-то случайные моменты времени. Обслуживание поступившей заявки продолжается некоторое (случайное) время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок, (они образуют очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или простаивать.

СМО в зависимости от числа каналов и их производительности, а также от характера потока заявок обладает какой-то пропускной способностью, позволяющей более или менее успешно справляться с потоком заявок. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и успешностью (эффективностью) обслуживания.

В качестве характеристик эффективности обслуживания, в зависимости от условий задачи и целей исследования, могут применяться различные величины и функции, например:

среднее количество заявок, которое может обслужить СМО в единицу времени;
средний процент заявок, получающих отказ и покидающих СМО необслуженными;
вероятность того, что поступившая заявка немедленно будет принята к обслуживанию;
среднее время ожидания в очереди;
закон распределения времени ожидания;
среднее количество заявок, находящихся в очереди;
средний доход, приносимый СМО в единицу времени, и т.п.

Случайный характер, как потока заявок, так и длительности обслуживания приводит к тому, что в СМО будет происходить какой-то случайный процесс. Случайный процесс (вероятностный, стохастический процесс) – случайная функция X(t) от независимой переменной t (время). Это такой процесс, течение которого может быть различным в зависимости от случая, причем вероятность того или иного течения определена. Случайный процесс дискретен или непрерывен в зависимости от того, дискретно или непрерывно множество его значений. Если дискретен аргумент t, говорят о процессе с дискретным временем или случайной последовательности. Если свойства процесса не зависят от начала отсчета времени, то такой процесс называется стационарным. Понятие случайных процессов широко используется в теории массового обслуживания, теории игр и т.д. Чтобы дать рекомендации по рациональной организации этого процесса и предъявить разумные требования к СМО, необходимо изучить случайный процесс, протекающий в системе, описать его математически. Этим занимается теория массового обслуживания. Область применения математических методов теории массового обслуживания непрерывно расширяется и все больше выходит за пределы задач, связанных с «обслуживающими организациями» в буквальном смысле слова. Как своеобразные системы массового обслуживания могут рассматриваться: информационно-вычислительные сети, операционные системы электронных вычислительных машин; системы сбора и обработки информации; автоматизированные производственные цехи, поточные линии; транспортные системы; системы противоздушной обороны и т.п.

Близкими к задачам теории массового обслуживания являются многие задачи, возникающие при анализе надежности технических устройств.

Математическое исследование СМО очень облегчается, если случайный процесс, протекающий в системе, является марковским. Марковский процесс – дискретный или непрерывный, случайный процесс X(t) называется марковским, если можно полностью задать с помощью двух величии: вероятности P(x,t) того, что случайная величина x(t) в момент времени t равна x и вероятности P(x₂,t₂| x₁,t₁) того, что величина x при t= t₁равна x₁, то при t= t₂ она равна x₂. P(x,t) – это распределение вероятности первого порядка для случайного процесса X(t), а P(x₂,t₂| x₁,t₁) – вероятность перехода из состояния x₁ при t₁ в состояние x2 при t₂. дискретные по времени и значению Марковские процессы называют цепями Маркова. Выделение Марковских процессов в отдельный класс связано с тем, что многие реальные процессы, например, в теории массового обслуживания, могут с хорошей точностью считаться Марковскими. Тогда удается сравнительно просто описать работу СМО с помощью аппарата обыкновенных дифференциальных (в предельном случае – линейных алгебраических) уравнений и выразить в явном виде основные характеристики эффективности обслуживания через параметры СМО и потока заявок.

a . b.

P₁₂ P₁₃

P₂₃

P₂₄P₂₅P₅₃

P₄₅

Граф состояний и переходов: a. – обычный b. – размеченный.

Пусть имеется система S с n дискретными состояниями: S₁, S_2, S₃, … S_n_. Каждое состояние изображается прямоугольником, а возможные переходы («перескоки») из состояния в состояние – стрелками, соединяющими эти прямоугольники.

Стрелками отмечаются только непосредственные переходы из состояния в состояние; если система может перейти из состояния S₁ в S₅ только через S₂, то стрелками отмечаются только переходы S₁ — S₂ и S₁ — S₅, но не S₁ — S₅.

Пусть система S – прибор, который может находиться в одном из пяти возможных состояний: S₁ – исправен, работает; S₂ – неисправен, ожидает осмотра; S₄ – осматривается; S₅ – ремонтируется; S₅ – списан. (ГСП системы показан на рис.1, а).

Основные понятия теории Марковских процессов.

Марковские цепи

Способы описания Марковского случайного процесса, протекающего в системе с дискретными состояниями, зависят оттого в какие моменты времени – заранее известные или случайные – могут происходить переходы («перескоки») системы из состояния в состояние.

Случайный процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, заранее фиксированные моменты времени: t₁, t₂, …, и т.д. В промежутки времени между этими моментами система S сохраняет свое состояние.

Случайный процесс называется процессом с непрерывным временем, если переход системы из состояния в состояние возможен в любой, наперед неизвестный, случайный момент t.

Рассмотрим Марковский процесс с дискретными состояниями и дискретным временем.

Пусть имеется система S, которая может находиться в состояниях S₁, S_2, S₃, … S_n, причем изменения состояния системы возможны только в моменты: t₁, t₂, …, t_к, … .

Назовем эти моменты «шагами» или «этапами» процесса и рассматривать случайный процесс, происходящий в системе S, как функцию целочисленного аргумента: 1, 2, …, к, …(номера шага).

Случайный процесс, происходящий в системе, состоит в том, что в последовательные моменты времени t₁, t₂, …, t_к, … система S оказывается в тех или других состояниях, ведя себя, например, следующим образом (в общем система может не только менять состояние, но и сохранять прежнее):

S₁ — S₃— S₃ — S₃— S₅ — S₄— S₄ — S₂— S₁ —… .

Условимся обозначать событие, состоящее в том, что после к шагов система находится в состоянии S_i. При любом к события , ,… ,… образуют полную группу и несовместны.

Процесс, происходящий в системе, можно представить как последовательность (цепочку) событий, например: , , , …

Такая последовательность событий называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния S_i в S_j не зависит от того, когда и как система пришла в состояние S_i.

Марковскую цепь можно описать с помощью вероятностей состояний. Пусть в любой момент времени (после любого к-го шага) система S может быть в одном из состояний S₁, S_2, S₃, … S_n, т.е. осуществится одно из полной группы несовместных событий: , ,… ,… . Обозначим вероятности этих событий для к-го шага через: , , …, ,…, .

Видно, что для каждого номера к …+ , так как это – вероятности несовместных событий, образующих группу.

Вероятности … называются вероятностями состояния.

В совокупности они образуют вектор: p^(к) = ( … ) (1).

Случайный процесс (Марковскую цепь) можно представить себе так, как будто точка, изображающая систему S, случайным образом перемещается (блуждает) по графу состояний, перескакивая из состояния в состояние в моменты t₁, t₂, …, t_к, …, а иногда (в общем случае) задерживаясь на какое-то число шагов в одном и том же состоянии.

Для любого шага (момента времени t₁, t₂, …, t_к, … или номера 1, 2, …, к, …) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из них равны нулю, если непосредственный переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии. Эти состояния называются переходными вероятностями Марковской цепи.

Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага. В противном случае Марковская цепь является неоднородной.

Рассмотрим однородную Марковскую цепь. Обозначим через Р_ij вероятность перехода за один шаг из состояния S_i в состояние S_j; Р_ii будет вероятность задержки системы в состоянии S_i. Запишем данные вероятности в форме квадратичной матрицы: (2). Некоторые из переходных вероятностей Р_ijмогут быть равны нулю, что означает невозможность перехода системы из i-го состояния в j-е за один шаг. По главной диагонали матрицы переходных вероятностей стоят вероятности Р_ij того, что система не выйдет из состояния S_i, а останется в нем.

Сумма членов, стоящих в каждой строке матрицы (2), должна быть равна единице, так как в каком бы состоянии система ни была перед к-м шагом события , ,… ,… несовместны и образуют полную группу.

При рассмотрении Марковских цепей часто удобно пользоваться ГСП, на котором у стрелок проставлены переходные вероятности, или «размеченным графом состояний».

На рис.1(b) проставлены не все переходные вероятности, а только те из них, которые не равны нулю и меняют состояние системы, т.е. Р_ij при i j; «вероятности задержки» Р₁₁, Р₂₂ и т.д. проставлять на графе излишне, так как каждая из них дополняет до единицы сумму переходных вероятностей, соответствующих стрелкам, исходящим из данного состояния. Например, для графа рис.1 b . Если из состояния S_i не исходит ни одной стрелки (переход из него ни в какое другое состояние невозможен), соответствующая вероятность задержки Р_ii равна единице.

Имея в расположении размеченный ГСП (или, что равносильно, матрицу переходных состояний) и зная начальное состояние, можно найти вероятности состояний … после любого (к-го) шага.

Предположим, что в начальный момент (перед первым шагом) система находится в каком-то определенном состоянии, например S_m. Тогда для начального момента (0) будем иметь: т.е. вероятности всех состояний равны нулю, кроме вероятности начального состояния S_m_,равной единице.

Найдем вероятности после первого шага. Перед первым шагом система заведомо находится в состоянии S_m. Значит, за первый шаг она перейдет в состояния S₁, S_2, …S_m, … S_n с вероятностями P_m_1, P_m₂,…P_mm,…,P_nn, находящимися в m-й строке матрицы переходных вероятностей. Таким образом, вероятности состояний после первого шага будут: p₁(1) = P_m₁, p₂=P_m₂,…,p_m(1)=P_mm,…,p_n(1)=P_mn (3). Найдем вероятности состояний после второго шага: . Будем вычислять их по формуле полной вероятности с гипотезами:

после первого шага система была в состоянии S₁;

после первого шага система была в состоянии S₂;

…………………………..

после первого шага система была в состоянии S_i;

…………………………..

после первого шага система была в состоянии S_n.

Вероятности гипотез известны (1); условные вероятности перехода в состояние S_i при каждой гипотезе тоже известны и записаны в матрице переходных вероятностей. По формуле полной вероятности получим:

(4) или (5)

Данное выражение может быть записано в вектор -матричной форме: р⁽²⁾= Р^Т*р⁽¹⁾ (6), где Р^Т – транспонированная матрица(2).

В формулах (4) – (5) суммирование распространяется формально на все состояния S₁, S_2, …S_m, … S_n; фактически учитывать надо только те из них, для которых переходные вероятности P_ij отличны о нуля, т.е. те состояния, из которых может совершиться переход в состояние S_i(или задержка в нем).

Таким образом, вероятности состояний после второго шага известны. Очевидно, после третьего шага они определяются аналогично: (7) и вообще после к-го шага: (8) или в матричной форме р^(к)= Р^Т*р^(к-1) (9).

Итак, вероятности состояний p_i(k) после k-го шага определяются рекуррентной формулой (8) через вероятности состояний после (k – 1)-го шага; те, в свою очередь, – через вероятности состояний после (k – 2)-го шага, и т.д.

Потоки событий. Уравнения Колмогорова.

Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени.

Примерами могут быть:

• поток вызовов на телефонной станции;

• поток включений приборов в бытовой электросети;

• поток грузовых составов, поступающих на железнодорож

ную станцию;

• поток неисправностей (сбоев) вычислительной машины;

• поток выстрелов, направляемых на цель, и т. д.

При рассмотрении процессов, протекающих в системе с дискретными состояниями и непрерывным временем, часто целесообразно представлять процесс так, как будто изменения состояний системы происходят под действием каких-то потоков событий (поток вызовов, поток неисправностей, поток заявок на обслуживание, поток посетителей и т. д.) Поэтому имеет смысл рассмотреть подробнее потоки событий и их свойства,

Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается на практике, но представляет определенный интерес как предельный случай.. Чаще приходится встречаться с потоками событий, для которых и моменты наступления событий, и промежутки времени между ними случайны.

Потоки событий, обладающие некоторыми простыми свойствами.

1. Стационарность. Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок зависит только от длины участка и не зависит от того, где именно на оси расположен этот участок.

Стационарность потока означает его однородность по времени; вероятностные характеристики такого потока не меняются в зависимости от времени. В частности, так называемая интенсивность (или «плотность») потока событий — среднее число событий в единицу времени — для стационарного потока должна оставаться постоянной. Это, разумеется, не значит, что фактическое число событий, появляющихся в единицу времени, постоянно, поток может иметь местные сгущения и разрежения. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера, а среднее число событий, попадающих на единичный участок времени, остается постоянным для всего рассматриваемого периода.

2. Отсутствие последействия. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой (или другие, если рассматривается больше двух участков).

В таких потоках события, образующие поток, появляются в последовательные моменты времени независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последействия, потому что причины, обусловившие приход отдельного пассажира именно в данный момент, а не в другой, как правило, не связаны с аналогичными причинами для других пассажиров. Если такая зависимость появляется, условие отсутствия последействия оказывается нарушенным.

3. Ординарность. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Ординарность означает, что события в потоке приходят поодиночке, а не парами, тройками и т. д.

Простейший поток

Рассмотрим поток событий, обладающий всеми тремя свойствами: стационарный, без последействия, ординарный. Такой поток называется простейшим (или стационарным пуассоновским) потоком. Название «простейший» связано с тем, что математическое описание событий, связанных с простейшими потоками, оказывается наиболее простым. Отметим, между прочим, что «самый простой», на первый взгляд, регулярный поток со строго постоянными интервалами между событиями отнюдь не является «простейшим» в вышеназванном смысле слова: он обладает ярко выраженным последействием, так как моменты появления событий связаны между собой жесткой функциональной зависимостью. Именно из-за этого последействия анализ процессов связанных с регулярными потоками, оказывается, как правило труднее, а не легче по сравнению с простейшими.

Простейший поток играет среди других потоков особую роль — можно доказать, что при суперпозиции (взаимном наложении) достаточно большого числа потоков, обладающих последействием (лишь бы они были стационарны и ординарны) образуется суммарный поток, который можно считать простейшим, и тем точнее, чем большее число потоков суммируется. Дополнительно требуется, чтобы складываемые потоки были сравнимы по интенсивности, т. е., чтобы среди них не было одного, превосходящего по интенсивности сумму все остальных.

Если поток событий не имеет последействия, ординарен, но не стационарен, он называется нестационарным пуассоновским потоком. В таком потоке интенсивность л (среднее число событий в единицу времени) зависит от времени: λ = λ(t), тогда как для простейшего потока λ = const.

Пуассоновский поток событий (как стационарный так и нестационарный) тесно связан с известным распределением Пуассона — число событий потока, попадающих на любой участок, распределено по закону Пуассона.

Уравнения Колмогорова

Вероятности состояний удовлетворяют определенного вида дифференциальным уравнениям, называемым уравнениями Колмогорова.

(1)

Эти уравнения для вероятностей состояний называются уравнениями Колмогорова.

Интегрирование этой системы уравнений дает искомые вероятности состояний как функции времени. Начальные условия берутся в зависимости от того, каково было начальное состояние системы S. Например, если в начальный момент времени (при t = 0) система S находилась в состоянии 5*,, то надо принять начальные условия: р(0) = (1,0,0,0)

В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак «минус», если в состояние — знак «плюс». Каждый член равен произведению плотности вероятности перехода, соответствующей данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.

Это правило составления дифференциальных уравнений для вероятностей состояний является общим и справедливо для любой непрерывной марковской цепи; с его помощью можно совершенно механически, без всяких рассуждений, записывать дифференциальные уравнения для вероятностей состояний непосредственно по размеченному графу состояний.

Составление уравнений Колмогорова.

Уравнения Колмогорова

(1)

Эти уравнения для вероятностей состояний называются уравнениями Колмогорова.

Опорные знания (основные понятия Марковских процессов):

случайный процесс,
Марковский процесс,
граф состояния,
поток событий,
простейший поток,
вероятность состояния

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени P_i=P_i(t). Особенно, интересен случай, когда система находится в предельном (стационарном) режиме, т.е. при t  ∞. Такие вероятности

называются финальными (предельными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы S конечно, и из каждого из них можно за конечное число шагов перейти в любое другое состояние, то финальные вероятности существуют.

Предельная вероятность P_i, состояния S_i, имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Пример:

Рассмотрим некоторую СМО, которая имеет следующий граф состояний:

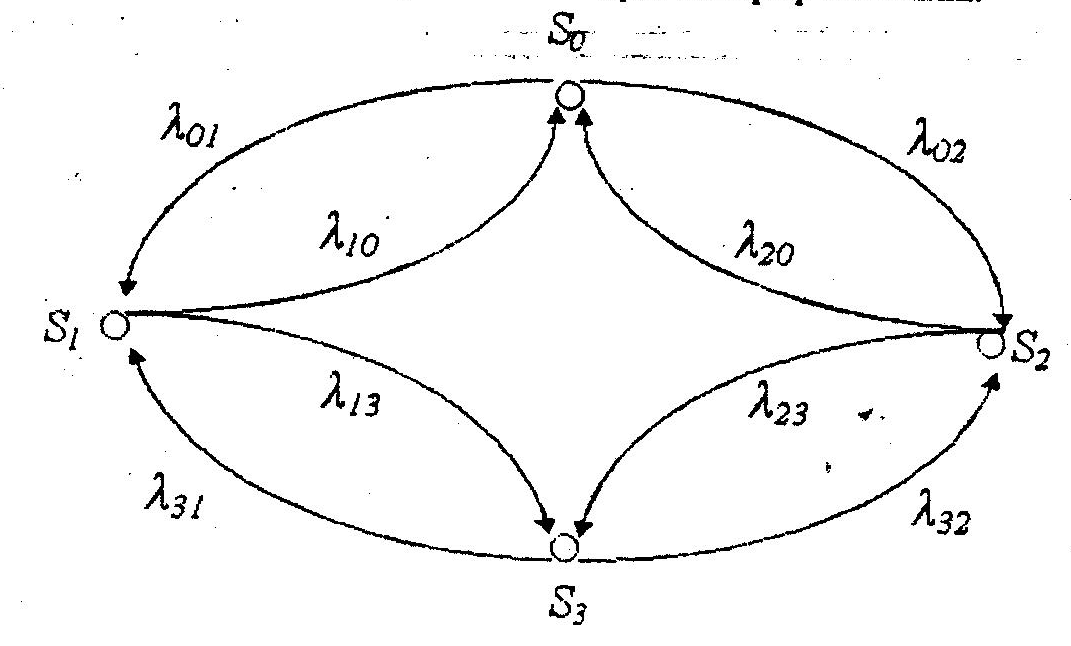
Предположим, что рассматриваемая система S имеет четыре возможных состояния S₀, S₁, S₂, S₃ а все переходы системы из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностям (i,j=0,1,2,3).

Вероятностью i-го состояния системы называется вероятностью p_i(t) того, что в момент t система будет находиться в состоянии S_i.

Очевидно, что для любого момента t сумма вероятностей всех состоянии равна единице:

Пусть Р₀= 0,5. Это означает, что в среднем половину времени система находится в состоянии S₀.

Система уравнений Колмогорова для стационарных режимов составляется непосредственно по провешенному графу состояний, если руководствоваться следующим правилом:

Слева в уравнениях стоит предельная вероятность данного состояния P_i умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа - сумма произведений интенсивностей всех потоков, входящих в i-ое состояние, на вероятности тех состояний, из которых эти потоки исходят.

Для данной СМО с указанным графом состояний такая система уравнений имеет вид:

( ₀₁+ ₀₂)P₀= ₁₀P₁+ ₂₀P₂

( ₁₀+ ₁₃)P₁= ₀₁P₀+ ₃₁P₃

( ₂₀+ ₂₃)P₀= ₀₂P₀+ ₃₂P₃

( ₃₁+ ₃₂)P₀= ₁₃P₁+ ₂₃P₂

Образец решения.

Найти предельные вероятности для системы S при условии, что матрица интенсивности потоков выглядит так:

Составим систему уравнений для предельных вероятностей состояний:

(1+2)*P₀=2*P₁+3*P₂

(2+2)*P₁=1*P₀+3*P₃

(3+1)*P₂=2*P₀+2*P₃

(3+2)*P₃=2*P₁+1*P₂

Преобразуем:

Приведем систему к стандартному виду:

Одно из первых четырех уравнений является следствием других трех уравнений, поэтому его можно исключить из системы.

Получаем систему четырех уравнений с четырьмя неизвестными. Решим систему методам Гаусса.

Расширенная матрица преобразована к треугольному виду, и по ней можно восстановить систему линейных уравнений:

Окончательно:

P₀=0,4 P₁=0,2 P₂=0,27 P₃=0,13

Таким образом, в предельном, стационарном режиме система S в среднем 40% времени будет находиться в состоянии S₀.

20% времени будет находиться в состоянии S₁

27% времени будет находиться в состоянии S₂

13% времени будет находиться в состоянии S₃

Понятие системы массового обслуживания. Классификация СМО.

СМО могут быть одноканальными или многоканальными.

среднее количество заявок, которое может обслужить СМО в единицу времени;
средний процент заявок, получающих отказ и покидающих СМО необслуженными;
вероятность того, что поступившая заявка немедленно будет принята к обслуживанию;
среднее время ожидания в очереди;
закон распределения времени ожидания;
среднее количество заявок, находящихся в очереди;
средний доход, приносимый СМО в единицу времени, и т.п.

a . b.

P₁₂ P₁₃

P₂₃

P₂₄P₂₅P₅₃

P₄₅

Граф состояний и переходов: a. – обычный b. – размеченный.

Системы массового обслуживания, их классы и основные характеристики. Для того чтобы процесс, протекающий в системе, был Марковским, нужно, чтобы все потоки событий, переводящие систему из состояния в состояние, были пуассоновскими (потоками без последействия). Для СМО потоки событий — это потоки заявок, потоки «обслуживании» заявок и т. д. Если эти потоки не являются пуассоновскими, математическое описание процессов, происходящих в СМО, становится несравненно более сложным и требует более громоздкого аппарата, доведение которого до аналитических формул удается только в простейших случаях.

Однако, аппарат «Марковской» теории массового обслуживания может пригодиться и в том случае, когда процесс, протекающий в СМО, отличен от марковского — с его помощью характеристики эффективности СМО могут быть оценены приближенно. Следует заметить, что чем сложнее СМО, чем больше в ней каналов обслуживания, тем точнее оказываются приближенные формулы, полученные с помощью марковской теории. Следует также заметить, что в ряде случаев для принятия обоснованных решений по управлению работой СМО вовсе и не требуется точного знания всех ее характеристик — зачастую достаточно приближенного, ориентировочного.

Основные классы СМО следующие.

1. Системы с отказами (с потерями). В таких системах заявка, поступившая в момент, когда все каналы заняты, получает «отказ», покидает СМО и в дальнейшем процессе обслуживания не участвует.

2.Системы с ожиданием (с очередью). В таких системах заявка, поступившая в момент, когда все каналы заняты, становится в очередь и ожидает, пока не освободится один из каналов. Когда канал освобождается, одна из заявок, стоящих в очереди, принимается к обслуживанию.

Обслуживание (дисциплина очереди) в системе с ожиданием может быть упорядоченным (заявки обслуживаются в порядке поступления), неупорядоченным (заявки обслуживаются в случайном порядке) или стековым (первой из очереди выбирается последняя заявка). Кроме того, в некоторых СМО применяется так называемое обслуживание с приоритетом, когда некоторые заявки обслуживаются в первую очередь, предпочтительно перед другими. Здесь также различаются системы со статическими и динамическими приоритетами (в последнем случае приоритет может, например, увеличиваться с длительностью ожидания заявки).

Системы с очередью делятся на системы с неограниченным и с ограниченным ожиданием.

В системах с неограниченным ожиданием каждая заявка, поступившая в момент, когда нет свободных каналов, становится в очередь и «терпеливо» ждет освобождения канала, который примет ее к обслуживанию. Любая заявка, поступившая в СМО, рано или поздно будет обслужена.

В системах с ограниченным о ж и д а н и е м на пребывание заявки в очереди накладываются те или другие ограничения. Эти ограничения могут касаться длины очереди (числа заявок, одновременно находящихся в очереди — система с ограниченной длиной очереди), времени пребывания заявки в очереди (после какого-то срока пребывания в очереди заявка покидает очередь и уходит — система с ограниченным временем ожидания), общего времени пребывания заявки в СМО и т. д.

В зависимости от типа СМО при оценке ее эффективности могут применяться те или другие величины (показатели эффективности). Например, для СМО с отказами одной из важнейших характеристик ее продуктивности является так называемая абсолютная пропускная способность — среднее число заявок, которое может обслужить система за единицу времени.

Наряду с абсолютной часто рассматривается относительная пропускная способность СМО — средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок).

Помимо абсолютной и относительной пропускной способностей при анализе СМО с отказами нас могут, в зависимости от задачи исследования, интересовать и другие характеристики, например:

• среднее число занятых каналов;

• среднее относительное время простоя системы в целом и

отдельного канала и т. д.

СМО с ожиданием имеют несколько другие характеристики. Очевидно, для СМО с неограниченным ожиданием как абсолютная, так и относительная пропускная способность теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Зато для такой С МО весьма важными характеристиками являются:

• среднее число заявок в очереди;

• среднее число заявок в системе (в очереди и под обслуживанием);

• среднее время ожидания заявки в очереди;

• среднее время пребывания заявки в системе (в очереди под обслуживанием);

и другие характеристики ожидания.

Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик: как абсолютная и относительная пропускная способности, так и характеристики ожидания.

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n, интенсивность потока заявок λ, производительность каждого канала (среднее число заявок ,и, обслуживаемое каналом в единицу времени)условия образования очереди (ограничения, если они есть).

В зависимости от значений этих параметров выражаются характеристики эффективности работы СМО.

Нахождение характеристик простейших систем массового обслуживания.

Наиболее легко поддаются анализу СМО с Марковскими процессами. Для того чтобы процесс, протекающий в системе, был марковским ,нужно, чтобы все потоки событий, переводящие систему из состояния в состояние, были пуассоновскими (потоками без последействия). Для СМО потоки событий — это потоки заявок, потоки «обслуживании» заявок и т. д. Если эти потоки не являются пуассоновскими, математическое описание процессов, происходящих в СМО, становится несравненно более сложным и требует более громоздкого аппарата, доведение которого до аналитических формул удается только в простейших случаях.

Основные классы СМО следующие.

Системы с очередью делятся на системы с неограниченным и с ограниченным ожиданием.

• среднее число занятых каналов;

• среднее относительное время простоя системы в целом и

отдельного канала и т. д.

• среднее число заявок в очереди;

• среднее число заявок в системе (в очереди и под обслуживанием);

• среднее время ожидания заявки в очереди;

• среднее время пребывания заявки в системе (в очереди под обслуживанием);

и другие характеристики ожидания.

В зависимости от значений этих параметров выражаются характеристики эффективности работы СМО.

Имитационное моделирование.

Выделяют две возможные цели имитационных экспериментов:

понять поведение исследуемой системы – потребность в этом часто возникает, например, при создании принципиально новых образцов продукции;
оценить возможные стратегии управления системой, что также очень характерно для решения широкого круга экономико- прикладных задач.

С помощью имитационного моделирования исследуют сложные системы. Методом имитационного моделирования исследуют системы, функционирующие во времени, что определяет необходимость создания и использования специальных методов (механизмов) управления системным временем.

Основные достоинства имитационного моделирования:

имитационная модель позволяет описать моделируемый процесс с большей адекватностью, чем другие;
имитационная модель обладает известной гибкостью варьирования структуры, алгоритмов и параметров системы;
применение ЭВМ существенно сокращает продолжительность испытаний по сравнению с натуральным экспериментом (если он возможен), а также их стоимость.

Основные недостатки:

решение, полученное на имитационной модели, всегда носит частный характер, так как оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы;
большие трудозатраты на создание модели и проведение экспериментов, а также обработку их результатов;
если использование системы предполагает участие людей при проведении машинного эксперимента, на результаты может оказать влияние так называемый «хаутонский эффект» (заключающийся в том, что люди зная и чувствуя, что за ними наблюдают, могут изменить поведение).

Имитационное моделирование предполагает работу с такими математическими моделями, с помощью которых результат исследуемой операции нельзя заранее вычислить или предсказать, поэтому необходим эксперимент (имитация) на модели при заданных исходных данных. В свою очередь, сущность машинной имитации заключается в реализации численного метода проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени.

Имитационная модель представляет собой комбинацию шести составляющих:

компонентов;
переменных;
параметров;
функциональных зависимостей;
ограничений;
целевых функций.

Структура имитационной модели

Составление расписание событий как способ организации квазипараллелизма получило широкое распространение в силу простоты и наглядности реализации.

Имитационная модель с календарем (расписанием) событий состоит из трех частей:

управляющей;
функциональной, состоящей из функциональных модулей;
информационной, включающей базу данных.

Управляющая часть содержит:

блок управления моделированием – предназначен для реализации принятого плана имитационного эксперимента;
блок диалога – предназначен для обеспечения комфортной работы пользователя с интерактивной моделью (в автоматических моделях этого блока нет);
блок обработки результатов моделирования – осуществляет обмен информацией с базой данных, и реализует процедуры расчета показателя эффективности. Если отсутствует блок диалога, на блок обработки возлагаются функции выдачи результатов моделирования на внешние устройства;
календарь событий – является важнейшим элементом имитационной модели, предназначенным для управления процессом появления событий в системе с целью обеспечения необходимой причинно-следственной связи между ними. Календарем событий решаются следующие основные задачи: ранжирование во времени плановых событий, вызов необходимых функциональных модулей в моменты наступления соответствующих событий, получение информационных выводных сигналов, их хранение и передача в нужные моменты времени адресатам.

Функциональная часть модели состоит из функциональных модулей, являющихся ее основными элементами. Именно в них описываются и реализуются все процессы в моделируемой системе. Обычно один функциональный модуль описывает либо отдельный ее элемент.

В функциональный модуль поступать пять видов входных сигналов:

стартовый сигнал (сигнал о начале моделирования);

сигнал о наступлении планового события;
информационный сигнал;
сигнал о прерывании моделирования;
сигнал об окончании моделирования.

Важнейшей задачей функционального модуля является планирование следующих событий, т.е. определение видов и ожидаемых моментов наступления. Для выполнения этой функции в функциональном модуле реализуется специальный оператор планирования. Для больших моделей остро стоит вопрос о «глубине планирования» т.е. о длительности интервала времени, на который прогнозируется наступление событий, поскольку для больших интервалов почти наверняка придется осуществлять повторное планирование после при хода очередного информационного сигнала.

Информационная часть имитационной модели. База данных представляет совокупность специальным образом организованных (структурированных) данных о моделируемой системе. Как правило, информация из БД выдается в другие части имитационной модели в автоматическом режиме. Наличие БД в имитационной модели не является обязательным и полностью, а определяется масштабами модели, объемами необходимой информации и требованиями по оперативности получения результатов моделирования и их достоверности. Если принято решение о включении БД в состав имитационной модели, проектирование БД не имеет каких-либо специфических особенностей.

Идея метода имитационного моделирования.

Выделяют две возможные цели имитационных экспериментов:

понять поведение исследуемой системы – потребность в этом часто возникает, например, при создании принципиально новых образцов продукции;
оценить возможные стратегии управления системой, что также очень характерно для решения широкого круга экономико- прикладных задач.

Основные достоинства имитационного моделирования:

имитационная модель позволяет описать моделируемый процесс с большей адекватностью, чем другие;
имитационная модель обладает известной гибкостью варьирования структуры, алгоритмов и параметров системы;
применение ЭВМ существенно сокращает продолжительность испытаний по сравнению с натуральным экспериментом (если он возможен), а также их стоимость.

Основные недостатки:

решение, полученное на имитационной модели, всегда носит частный характер, так как оно соответствует фиксированным элементам структуры, алгоритмам поведения и значениям параметров системы;
большие трудозатраты на создание модели и проведение экспериментов, а также обработку их результатов;
если использование системы предполагает участие людей при проведении машинного эксперимента, на результаты может оказать влияние так называемый «хаутонский эффект» (заключающийся в том, что люди зная и чувствуя, что за ними наблюдают, могут изменить поведение).

Имитационная модель представляет собой комбинацию шести составляющих:

компонентов;
переменных;
параметров;
функциональных зависимостей;
ограничений;
целевых функций.

Структура имитационной модели

Имитационная модель с календарем (расписанием) событий состоит из трех частей:

управляющей;
функциональной, состоящей из функциональных модулей;
информационной, включающей базу данных.

Управляющая часть содержит:

блок управления моделированием – предназначен для реализации принятого плана имитационного эксперимента;
блок диалога – предназначен для обеспечения комфортной работы пользователя с интерактивной моделью (в автоматических моделях этого блока нет);
блок обработки результатов моделирования – осуществляет обмен информацией с базой данных, и реализует процедуры расчета показателя эффективности. Если отсутствует блок диалога, на блок обработки возлагаются функции выдачи результатов моделирования на внешние устройства;
календарь событий – является важнейшим элементом имитационной модели, предназначенным для управления процессом появления событий в системе с целью обеспечения необходимой причинно-следственной связи между ними. Календарем событий решаются следующие основные задачи: ранжирование во времени плановых событий, вызов необходимых функциональных модулей в моменты наступления соответствующих событий, получение информационных выводных сигналов, их хранение и передача в нужные моменты времени адресатам.

В функциональный модуль поступать пять видов входных сигналов:

стартовый сигнал (сигнал о начале моделирования);

сигнал о наступлении планового события;
информационный сигнал;
сигнал о прерывании моделирования;
сигнал об окончании моделирования.

Генерация случайных чисел.

Общая схема метода Монте-Карло. Пусть необходимо вычислить какую-то величину m, рассматривая величину ξ такую, что ее математическое ожидание равно: Мξ = m. При этом дисперсия данной случайной величины Dξ = b. Рассмотрим N случайных независимых величин ξ₁, ξ₂,… ξ_N, причем их распределения совпадают с распределением случайной величины ξ.

Тогда распределение суммы ρ_N= ξ₁ + ξ₂+,…+ ξ_N приблизительно нормальное со средним, равным μ = Nm, и дисперсией σ² = Nb². тогда расчет и оценка m погрешности метода производится по формуле: .

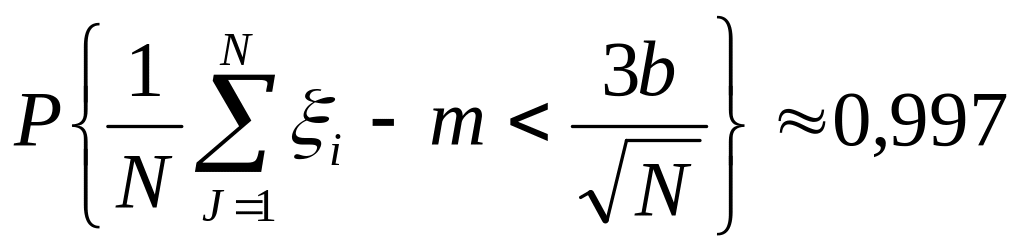Сущность применения метода Монте-Карло заключается в определении результатов на основании статистики, полученной к моменту принятия решения. Достоверность результатов, полученных с помощью метода Монте-Карло, определяется качеством генератора случайных чисел, т.е. некоторая случайная величина вычисляется с помощью последовательности равномерно распределенных случайных чисел, заключенных в интервале от 0 до 1 и выбранных в соответствии с функцией распределения: , где — вероятность того, что величина Х принимает значение меньше х.

При таком распределении возможно появление значений случайной величины из рассматриваемого интервала.

Основной метод получения случайных чисел – генерация по модулю, т.е. псевдослучайное число х последовательности {x_i} получается согласно рекурсивному соотношению: x_i = ax_i_-1 + c(mod m), где m,a, c, x₀ – целые положительные числа и m, x₀. неудачный выбор величин m, a, c приводит к ошибкам при моделировании методом Монте-Карло. При численном моделировании необходимо большое количество случайных чисел. Значит за период последовательности генерируемых случайных чисел должен быть достаточно большим, гораздо больше требуемого количества случайных чисел, чтобы результаты моделирования не искажались.

Построение генератора случайных чисел происходит с учетом следующих принципов (для машинного языка программирования).

начальное число Х выбирается произвольно.
число m должно быть большим (например 2³⁰), так как оно определяет период генерируемой псевдослучайной последовательности.
число а выбирается таким образом, чтобы а mod 8 = 5 при m равным степени двойки или а mod 10 = 21 при m равным степени 10. при этом генератор будет вырабатывать все m возможных значений еще до начала повторения.
двоичные или десятичные цифры числа а не должны иметь простую регулярную структуру, само число а должно лежать в интервале: 0,01m < a < 0.99m.
значение числа с не должно иметь общего множителя с числом m.
можно генерировать не больше m/1000 случайных чисел, при дальнейшей генерации выбирается новый множитель а.

При программировании на языках высокого уровня число m выбирается простым, близким к максимальному легко вычисляемому целому числу, число а берется равным первообразному корню их m, число с = 0. Например, а = 48 271, m = 2³¹ – 1.

Применение метода имитационного моделирования к простейшим задачам управления запасами.

Управление запасами — комплекс моделей и методов, предназначенных для оптимизации запасов, т. е. ресурсов, находящихся на хранении и предназначенных для удовлетворения спроса на эти ресурсы. Термины ресурсы и з а п а сы здесь понимаются обобщенно: можно говорить о запасах конечной продукции, о запасах полуфабрикатов (тогда соответствующая задача будет задачей об оптимизации незавершенного производства), о запасах сырья, природных и трудовых ресурсов, денежных средств и т. д. Роль производства сводится здесь к пополнению уровня запасов по мере возникновения потребности в них. Другим источником удовлетворения заявок на ресурсы является склад, собственно запас.

В качестве целевой функции в задачах управления запасами выступают суммарные затраты на содержание запасов, на складские операции, потери от порчи при хранении и моральное старение, потери от дефицита и штрафы и т. д. Естественно, что отыскивается минимум этой функции. Управляемыми переменными в таких задачах являются объем запасов, частота и сроки их пополнения (путем производства, закупки и т. д.), степень готовности продукции, хранящейся в виде запасов и др. Задачи бывают статические (когда принимается разовое решение об уровне запаса на определенный период) и динамические, или многошаговые, когда принимаются последовательные решения или корректируется ранее принятое решение с учетом происходящих изменений.

Упрошенным примером задач управления запасами может служить задача об оптимальной партии.

Теория игр — раздел, изучающий математические модели__

А н а л и т и ч е с к о е м о д е л и р о в а н и е сложных систем, очевидно, имеет ограниченные возможности, что и вызвало к жизни и м и т а ц и о н н ы е модели (реализуемые в форме аппаратурных комплексов и программ для ЭВМ). Могут быть выделены следующие основные классы имитационных моделей:

• непрерывные;

• дискретные;

• пространственные.

В первом случае предметная область описывается совокупностью динамических связей, отражающих развитие процесса во времени в форме конечно-разностных уравнений и рекуррентных соотношений. Модель воспроизводит поведение объекта за определенный период времени; в этом смысле имитационная модель является динамической. Значения всех переменных, входящих в имитационную модель, вычисляются в каждый момент модельного времени. Затем, через определенный интервал на основе старых значений вычисляются новые значения переменных, и т. д. Таким образом, имитационная модель «развивается» по определенной траектории в течение заданного отрезка модельного времени. Исходные аналитические модели — системы о б ы к н о в е н н ы х д и ф ф е р е н ц и а л ь н ы х уравнений.

Второй тип моделей описывает потоки случайных событий, проходящие через сложную совокупность путей и узлов, и направлен на исследование стационарных, установившихся процессов.

Здесь в качестве аналитического прототипа выступает теория с и с т ем м а с с о в о г о обслуживания.

В третьем случае рассматриваются процессы, проходящие впространстве (на плоскости или в объеме). Исходные аналитические модели — системы д и ф ф е р е н ц и а л ь н ы х уравнений в частных производных, особенно часто — такой их класс, как у р а в н е н и я м а т е м а т и ч е с к о й физики.

Следует отметить, что в настоящее время данная классификация во многом становится условной, поскольку современные интегрированные средства моделирования — ИСМ (например, отечественная разработка Pilgrim и ее зарубежные аналоги) охватывают как непрерывные, так и дискретные, и пространственно-временные процессы.

Модели системной динамики

В классической работе Дж. Форрестера в начале 1970-х гг. была построена математическая модель мировой динамики. Мировая система в этой модели описывается следующими переменными: население Земли Р, капитал К, доля капитала в сельском хозяйстве X, загрязнение Z\\ запасы не возобновляемых природных ресурсов R. Динамику этих переменных определяет система дифференциальных уравнений

Компьютерный анализ этой системы показал, что при сохранении тенденций развития глобальной системы, имевших место в начале 70-х гг., рост населения Р, капитала К, материального обеспечения приведет к истощению невозобновляемых ресурсов, чрезмерному загрязнению Земли и сменится быстрым падением численности населения и упадком производства. В качестве альтернативы такому упадку Дж. Форрестер предлагал перейти к глобальному равновесию, которое понималось им как выход переменных модели на стационарные значения.

Общепризнано, что работы Дж. Форрестера положили начало направлению с и с т е м н а я д и н а м и к а .

Системная динамика представляет собой совокупность принципов и методов анализа динамических управляемых систем с обратной связью и их применения для решения производственных, организационных и социально-экономических задач. Три достижения, обеспеченные в основном благодаря разработкам в области вооружений, сделали возможным применение системной динамики:

• успехи в проектировании и анализе систем управления с

обратной связью;

• прогресс в методах компьютерного моделирования и развитие

вычислительной техники;

• накопленный опыт в моделировании процесса принятия

решений.

Методология системной динамики базируется на предположении, что поведение (или история развития во времени) организации главным образом определяется ее информационно-логической структурой. Она отражает не только физические и технологические аспекты производственных процессов, но, что гораздо важнее, политику и традиции, которые явно или неявно определяют процесс принятия решений в организации. Такая структурная схема содержит источники усиления временных задержек и информационных обратных связей, подобных тем, которые встречаются в сложных инженерных системах.

Другой аспект системной динамики заключается в предположении, что организация более эффективно представляется в терминах лежащих в ее основе потоков, нежели в терминах отдельных функций. Потоки людей, денег, материалов, заявок и оборудования, а также интегрированные потоки информации могут быть выявлены во всех организациях. Направленность на потоковую структуру заставляет аналитика естественным образом преодолевать внутриорганизационные границы.

Для описания сложных систем с обратными связями используются четыре основных понятия: переменная, связь, цикл обратной связи, система с обратными связями:

• п е р е м е н н а я представляет собой количество некоторого продукта, которое изменяется во времени. Переменная может выражать решение, например, «объем дополнительных ресурсов», или показывать результат ранее принятого решения, например «затраты». Если переменная не изменяется в зависимости от изменения других переменных системы, она называется «экзогенной», т. е. внешней для системы. Переменная, значение которой изменяется в зависимости от изменения других переменных внутри системы, называется «эндогенной»;

• с в я з ь отражает причинно-следственные соотношения между двумя переменными. Графически се легко себе представить как стрелку, в начале которой лежит исходная переменная, а на конце — зависимая переменная;

• цикл с о б р а т н о й с в я з ью в простейшем случае можно представить как совокупность двух переменных и двух связей, такую, что начальная переменная сначала влияет на значение зависимой (прямая связь), а та, в свою очередь, влияет на значение исходной (обратная связь). Характерным

для такого цикла является наличие временных задержек: сначала задержка между решением и следствием от него, а затем, задержка между следствием и тем моментом времени, когда информация об этом следствии повлияет на новое решение;

• с и с т е м а с обратными с в я з я м и — совокупность связанных между собой циклов с обратными связями. Поведение переменной, входящей в один цикл с обратной связью, может влиять на поведение другой переменной, входящей в другой цикл. Сложные задачи управления, представляемые в виде таких систем, могут состоять из большого числа циклов. Именно такие сложные системы с большим числом циклов и составляют предмет изучения системной динамики. По мере усложнения системы соответственно возрастает сложность получения формального аналитического решения. Поэтому для анализа таких систем применяется имитационное моделирование.

Для построения имитационных моделей динамических систем используются переменные четырех типов — время, фонд, поток и конвертор:

• время является первичной переменной для имитационной модели динамической системы: ее значение генерируется системным таймером и изменяется дискретно, т. е., начиная с некоторого начального значения, время за каждый такт увеличивается на заранее заданную величину, которая служит единицей модельного времени. Число тактов и единица времени являются параметрами «прогона» модели и определяются заранее;

• фонд — переменная, равная объему (количеству) некоторого «продукта», накопленного в некотором хранилище за время «жизни» модели с начального по текущий момент. Продукт может поступать в фонд и/или извлекаться из него. Поэтому значение фонда в текущий момент времени можно вычислить как сумму его значения в предыдущий момент и величины, равной разности величин входящего.и исходящего потоков продукта за единицу модельного времени. Помимо очевидных примеров, таких, как фонды материальных и людских ресурсов, переменные этого типа могут характеризовать объемы накопленной информации, служить оценкой субъективных вероятностей наступления некоторых событий к определенному моменту времени, выражать меру влияния одних субъектов некоторого процесса на другие. Средние величины всех видов также можно рассматривать как информационные фонды специального вида;

•поток —переменная, равная объему (количеству) продукта, который поступает или извлекается из соответствующего фонда в единицу модельного времени. Значение этой переменной может изменяться в зависимости от внешних воздействий на нее. В частности, поток можно представить ак функцию от значений других потоков и фондов. Простейший пример цикла с обратной связью образует входящий поток, величина которого зависит от значения фонда, в который этот поток поступает.

Фонды характеризуют статическое состояние системы, а потоки —ее динамику. Если, например, представить себе, что в какой-то момент времени все процессы в системе остановятся, то фонды будут иметь те значения, которые были на момент остановки, а потоки будут равны нулю. С другой стороны, о величине потока можно судить только за определенный промежуток времени.

Помимо фондов и потоков, при построении имитационных моделей динамических систем используются вспомогательные переменные —конверторы. Эти переменные могут быть равны константам или значениям математических функций от других переменных (в том числе и от переменной время), т. е. позволяют преобразовывать (конвертировать) одни числовые значения в другие.

Применение метода имитационного моделирования к простейшим задачам теории массового обслуживания.

Имитационное моделирование систем массового обслуживания (СМО) включает имитацию входных потоков и обслуживающих приборов для изучения характеристик работы системы на интервале моделирования.

Система массового обслуживания характеризуется следующими показателями: долей времени занятости приборов, числом обслуживаний, максимальной длиной очереди, средней длиной очереди, средней продолжительностью одного обслуживания, общим числом входов в очередь без последующего ожидания, средним временем, проведенным в очереди и некоторым другим.

К моделированию СМО есть два подхода:

1. Разбиение временного промежутка моделирования на малые дискретные промежутки, на каждом из которых затем с помощью соответствующих датчиков бернулиевых случайных величин рассматривается одно из событий, а потом производится проверка, не является ли рассматриваемый дискрет последним.

2. По наступлению критических событий, т.е. просматриваются только моменты прихода заявок и окончания обслуживания и проверяется, не истекло ли время моделирования.

При имитационном моделировании по наступлению критических событий на интервале имитации последовательно моделируются моменты критических событий в процессе выполнения некоторых стандартных шагов – тактов. Главными величинами являются: значение ближайшего для данного такта момента окончания обслуживания заявки прибором и значение ближайшего момента прихода заявки. Эти величины меняются от такта к такту, и согласованное изменение и х составляет суть их имитации.

В системе в установившемся режиме среднее время ожидания (пребывания в системе) не зависит от правила выбора из очереди. В частности, при случайном равновероятностном выборе и при инверсном выборе (при освобождении прибора на обслуживание поступает требование, пришедшее последним) среднее время ожидания то же, что и при обслуживании в порядке очереди.

Однако это свойство нарушается при обслуживании с прерыванием в системе, где при поступлении нового требования текущее обслуживание прерывается, а при окончании обслуживания из очереди выбирается поступившее последним требование.

Методы и приемы прогнозирования.

В прогнозировании большое значение имеет выбранный метод, а также прием.

Прием прогнозирования — это одна или несколько математических или логических операций, направленных на получение конкретного результата при прогнозировании. В качестве примеров таких приемов можно назвать сглаживание или выравнивание динамических рядов, расчет средневзвешенного значения величин.

Метод прогнозирования — это способ исследования объекта прогнозирования, направленный на разработку прогноза. Совокупность специальных правил, приемов и методов составляет методику прогнозирования.

К наиболее распространенным методам прогнозирования относятся: экстраполяция, нормативные расчеты, в том числе интерполяция, экспертные оценки, аналогия, математическое моделирование.

Экстраполяция — это метод, при котором прогнозируемые показатели рассчитываются как продолжение динамического ряда на будущее по выявленной закономерности развития. По существу экстраполяция является -переносом закономерностей и тенденций прошлого на будущее на основе взаимосвязей показателей одного ряда. Метод позволяет найти уровень ряда за его пределами в будущем. Экстраполяция эффективна для краткосрочных прогнозов, если данные динамического ряда выражены ярко и устойчиво.

Экстраполяция называется формальной экстраполяцией, если предполагается сохранение прошлых и настоящих тенденций развития на будущее. Если же фактическое развитие увязывается с гипотезами о динамике процесса развития с учетом физической и логической сущности, то говорят о прогнозной экстраполяции. Она может быть в виде тренда, огибающих кривых, корреляционных и регрессионных зависимостей, может быть основана на факторном анализе и др. Экстраполяция сложного порядка может перерасти в моделирование.

Нормативный метод прогнозирования заключается в определении путей и сроков достижения возможных состояний явления, принимаемых в качестве цели. Речь идет о прогнозе достижения желаемых сочетаний явления на основе заранее заданных норм, идеалов, стимулов и целей. Такой прогноз отвечает на вопрос: каким путем или путями можно достичь желаемого состояния системы.

Нормативный метод чаше применяется для программных или целевых прогнозов. Используются как количественное выражение норматива, так и определенная шкала возможностей оценочной функции.

Метод экспертных оценок используется преимущественно в

долгосрочных прогнозах. В качестве эксперта выступает квалифицированный

специалист (группа специалистов) по конкретной проблеме, который может сделать (долгосрочный) достоверный вывод об объекте прогнозирования. Метод чаще используется в тех случаях, когда трудно количественно оценить прогнозный фон, и специалисты делают это на основе своего понимания вопроса. По существу мнение специалиста — это результат мысленного анализа и обобщения процессов, относящихся к прошлому, настоящему и будущему, на основании своего собственного опыта, квалификации и интуиции.

Метод экспертных оценок имеет несколько видов:

• индивидуальная экспертная оценка;

• коллективная экспертная оценка;

• метод генерации идей;

• аналитический метод;

• метод интервью;

• метод экспертных комиссий;

• дельфийский метод;

• метод коллективной генерации идей;

• синоптический метод и др.

Метод аналогии предполагает перенос знаний об одном предмете (явлении) на другой. Такой перенос верен с определенной долей достоверности (вероятности), так как сходство между явлениями редко бывает полным. Различают аналогию историческую и математическую. Историческая аналогия основана на установлении и использовании аналогии объекта прогнозирования с одинаковыми по природе объектами, которые опережают прогнозируемые в своем развитии.

Метод математической аналогии основан на установлении аналогии математических описаний процессов развития различных по природе объектов с последующим использованием более изученного и более точного математического описания одного из них для разработки прогнозов другого. Этот метод используется в экономико-математическом моделировании и при экспериментальном подходе к изучению экономики, когда знание о признаках одного предмета возникает на основании его сходства с другими предметами. Моделирование и эксперимент обязательно используют метод аналогии.

Моделирование (математическое моделирование) означает описание экономического (моделируемого) явления посредством математических формул, уравнений и неравенств. Математический аппарат должен достаточно точно отражать прогнозный фон, хотя полностью отразить всю глубину и сложность прогнозируемого объекта довольно трудно. В широком смысле модель — это заместитель оригинала (объекта исследования), имеющий с ним такое сходство, которое позволяет получить новое знание об объекте. При более узком понимании модели она рассматривается как объект прогнозирования. Ее исследование позволяет получить информацию о возможных состояниях объекта в будущем и путях достижения этих состояний.

С помощью математических моделей определяют:

• зависимость между различными экономическими показателями;

• различного рода ограничения, накладываемые на показатели;

• критерии, позволяющие оптимизировать процесс.

В прогнозировании различают: макромоделирование, т. е. укрупненное моделирование показателей экономики развития страны в целом; микромоделирование, т. е. построение моделейдля отдельного объекта (фирмы); моделирование на мезоуровне, характеризующем моделирование экономических процессов региона, отрасли.

Возможности экономико-математического моделирования весьма широки — от анализа до выработки управленческого решения, включая вопросы прогнозирования развития хозяйственных процессов. Однако нельзя переоценивать значение моделирования. Моделирование обычно рекомендуется использовать как «консультирующее средство», но окончательное решение всегда должно оставаться за специалистом. Сложное экономическое явление (процесс) требует создания (разработки) сложных математических моделей, а они, в свою очередь, приводят к трудностям в расчетах. При упрощении модели возможно снижение ее достоверности.

Эти два полюса (две крайности) должны учитываться прогнозистом при использовании метода моделирования. Методы прогнозирования не исчерпываются перечисленными выше. Существуют иные методы и подходы:

•морфологический анализ;

•прогнозный сценарий;

•прогнозный граф и «дерево целей»;

•корреляционный и регрессионный анализ;

•метод группового учета аргументов;

•факторный анализ;

• теория распознавания образов;

• вариационное исчисление;

• спектральный анализ;

• цепи Маркова;

• элементы алгебры логики;

• теория игр и др.

Таким образом, существуют различные типовые методы прогнозирования. Задача прогнозиста — выбрать такой метод, который в наибольшей мере соответствовал бы задачам и принципам прогнозирования данного явления (объекта).

Классификация прогнозов.

Сущность и классификация прогнозов

1. Прогноз является следствием действительности как единого целого, а будущее, отражаемое в прогнозе, — это результат сложного комплекса причин и условий. Прогноз — это итог выводов, эмпирических данных и обоснованных предположений, представляет аргументированное заключение о направлениях развития в будущем.

2. Возникновение будущего как следствия реальных событий содержит элемент случайности. Поэтому прогноз должен иметь оценку степени вероятности наступления события.

3. Прогноз, обладающий потенциалом будущего, испытывает влияние различных признаков действительности или моделирует эти признаки. При отсутствии изученных закономерностей развития для прогноза используется гипотеза о закономерностях.

4. Для составления прогноза необходимы научные исследования количественного и качественного характера, включая количественную

оценку на будущее.

5. Прогноз является ориентиром для планирования, создает исследовательскую основу для подготовки плана.

6. Прогноз носит вероятностный характер, и является многовариантным

7. Временные и пространственные горизонты прогноза зависят от сущности рассматриваемого явления, он удобен как итеративный, т. е. повторяющийся и непрерывный процесс.

8. При разработке прогноза не ставятся конкретные задачи и исключается детализация.

9. Точность прогноза проверяется временем.

10. При разработке прогноза от специалиста требуются прежде всего объективность и научная добросовестность, субъективизм оценке прошлого, настоящего и будущего не допускается.

В основе прогноза лежит научное предвидение. Научное предвидение может иметь форму предсказания , которому присущ описательный характер, или предуказания , когда указываются необходимые действия для достижения цели.

Прогноз не просто интерпретирует закономерности и внешние условия развития, а используется для поиска нужных решений. Он может рассматриваться как начальная стадия планирования, определяющая выбор путей достижения целей этого плана. В дополнение к ранее указанным общим характеристикам прогноза отметим, что экономический прогноз позволяет:

• оценить состояние и осуществить поиск возможных вариантову правленческих решений;

• определить область для направления изменения будущих событий;

• выявить проблемы, слабо выраженные в настоящем, но возможные в будущем;

• осуществить поиск вариантов активного воздействия на объективные факторы будущего;

• смоделировать варианты событий при учете ведущих факторов.

Назначение прогноза выражается в его функциях. К основным функциям прогноза относятся:

• анализ социально-экономических и научно-технических процессов и тенденций, объективных причинно-следственных связей этих явлений в конкретных условиях, в том числе оценка сложившейся ситуации и выявление проблем хозяйственного развития;

• оценка этих тенденций в будущем, предвидение новых экономических условий и проблем, требующих разрешения;

• выявление альтернативы развития в перспективе, накопление экономической информации и расчетов для обоснования выбора и принятия оптимального управленческого решения.

Принцип прогнозирования характеризует основную идею теории, или исходное положение. К основным принципам прогнозирования относятся: системность, согласованность, вариантность, непрерывность, верифицируемое™ и эффективность:

• системность означает требование взаимоувязанное и соподчиненное объекта прогнозирования, прогнозного фона и элементов прогнозирования, т. е. прогнозирование — сложный процесс, реализуемый системой;

• согласованность означает необходимость согласования поисковых и нормативных прогнозов различной природы (признаков) и различного срока упреждения времени;.

• вариантность в прогнозировании означает требование разработки вариантов прогнозного фона;

• непрерывность означает необходимость корректировки прогноза по мере поступления новой информации об объекте прогнозирования;

• верифицируемость — т. е. определение достоверности, точности и обоснованности прогноза;

• эффективность определяет необходимость превышения экономического эффекта от использования прогноза над затратами по его разработке.

В соответствии с проблемно-целевым признаком различают прогнозы поисковый и нормативный:

• поисковый прогноз (или исследовательский, трендовый, генетический)— это прогноз определения возможных состояний явления в будущем, отвечающий на вопрос: что вероятнее всего произойдет при условии сохранения действующих тенденций. Его метод — экстраполяция.

• нормативный прогноз (или программный, целевой) выполняется с целью определения путей и сроков достижения возможных состояний объекта прогнозирования в будущем, принимаемых в качестве цели. Основной метод прогнозирования — интерполяция.

По критерию природы объекта выделяют прогнозы:

• социальные (в том числе демографические);

• ресурсные (природные, материальные, трудовые, финансовые);

• научно-технические (перспективы развития науки и техники и влияние этих достижений на экономику);

• общественных и личных потребностей (спрос, потребление, потребности в образовании, здравоохранении, правопорядке, культуре и т. д.).

По критерию времени выделяют прогнозы: оперативные (до одного месяца); краткосрочные (от двух месяцев до года); среднесрочные (от 1 до 5 лет); долгосрочные (от 5 до 15 лет); даль несрочные (свыше 15 лет).

По критерию сложности различают прогнозы: сверхпростой, простой, сложный, сверхсложный. Эти прогнозы отличаются наличием взаимосвязанных переменных в их описании: в сверхпростом прогнозе отсутствуют существенные взаимосвязи, в сверхсложном — взаимосвязи тесные (с коэффициентом корреляции, близким к 1).

По степени детерминированности объекта прогнозы могут быть: детерминированными, т. е. без существенных потерь информации в описании условий; стохастическими, в которых требуется учет случайных величин; смешанными, включающими характеристики двух вышеуказанных прогнозов.

По критерию характера развития объекта во времени различаются прогнозы: дискретные, для которых характерен тренд со скачкообразными изменениями в фиксированные периоды времени; апериодические, которые представлены в виде непериодических функций времени; циклические, для которых характерна периодическая функция времени.

По критерию масштабности объекта различают прогнозы: сублокальные; локальные; суперлокальные (субглобальные); глобальные. Если говорить об отдельной фирме или объединении предприятий, то речь должна идти, как правило, о первых трех видах, а для стран или групп стран более характерны глобальные прогнозы.

Системы прогнозирования.

Прогнозирование как целенаправленный процесс должно реализовываться (осуществляться) в системе. В зависимости от масштаба и целей прогнозирования различают следующие системы:

• мирохозяйственная система;

• государственная система;

• отраслевая система;

• региональная система;

• межфирменная система (межфирменный проект);

• внутрифирменная система;

• система прогнозирования отдельной сферы деятельности,параметра, показателя.

Функционирование системы связано с периодической разработкой прогнозов и их корректировкой. Конечно, прогнозирование масштабной системы отличается от прогнозирования на уровне фирмы. Несмотря на многообразие организационных форм (видов) систем прогнозирования, в любой из них обязательно должны присутствовать следующие компоненты (составные части):

• объекты прогнозирования (явления, процессы, виды хозяйственной деятельности и т. д.);

• специалист (коллектив специалистов), осуществляющий прогнозирование;

• технические средства (ЭВМ, модели, алгоритмы и т. д.);

• метод (совокупность методов) прогнозирования;

• организационные мероприятия (управление процессом прогнозирования).

Коллектив специалистов, т. е. исполнителей работы, может включать специалистов в сфере экономики, финансов, маркетинга, менеджмента, социологии, технологии и ряда других областей знаний. Усилиями этих специалистов выполняется работа в соответствии с действующей методологией прогнозирования.

Рассматривая систему прогнозирования, необходимо учесть следующие элементы, обеспечивающие ее функционирование:

• система входной информации — вход в систему;

• прогнозный фон — совокупность внешних факторов, воздействие которых необходимо учитывать при прогнозировании;

• целевая функция — выход системы прогнозирования, то, ради чего создается система и осуществляется прогноз.

Следует остановиться, учитывая их роль и вес, на системе информации (вход системы прогнозирования) и организации прогнозирования (управление).

Система информации — это один из основных элементов системы прогнозирования, представляющий собой совокупность исходных данных, предпосылок, требований к прогнозу и т. д.

Х = (х₁, х₂, …, x_n), где x_i, i= 1, ..., п, — составляющая, элемент совокупности, последовательности. Расчет прогноза должен опираться на такую информацию по проблеме, которая существенно опережает по времени реально протекающий процесс развития. Желательно, чтобы временной лаг опережения информации составлял более 10 лет. Величина минимального опережения информации является условием эффективности использования самого прогноза. Она позволяет уменьшить неопределенность знаний о каком-либо явлении, событии. Для задач прогнозирования требуется создание лишь определенного массива информации. Он представляет собой совокупность данных об объекте прогнозирования, приведенных в соответствие с задачами и методами прогнозирования. Здесь важны качество и надежность исходной информации. В прогнозировании различают четыре категории надежности информации:

1-я категория — надежные ожидания, т. е. имеется полная и точная информация. Такая ситуация благоприятна для прогноза, но редко встречается;

2-я категория — рискованные ожидания, т. е. имеющаяся информация не является достаточно надежной. В таком случае рекомендуется выполнить расчет с целью определения ее отклонения от предполагаемой;

3-я категория — субъективно ненадежные ожидания, т. е. имеющаяся информация является неточной и ненадежной, но получить новую невозможно;

4-я категория — объективно ненадежные ожидания. В этом случае говорят об отсутствии данных для оценки возможного реального, развития события.

При прогнозировании может использоваться следующая информация:

• фактографическая, содержащая фактические данные;

• экспертная, содержащая экспертные оценки для достижения задач прогноза;

• научно-техническая;

• информация по переменной объекта прогнозирования, т. е. содержащаяся в значениях переменной.

Информация прогнозного фона должна учитывать происходящие изменения в окружающей среде, в том числе: социально экономические, технические, технологические, политические факторы, оказывающие влияние на объект прогнозирования.

Организация прогнозирования. Основа функционирования системы прогнозирования (независимо от ее сложности) — это организация прогнозирования или управление процессом прогнозирования. Как и любое управление, организация прогнозирования включает (в общем случае):

• планирование;

• оперативное управление, связанное с корректировкой ранее принятых решений (планов) с учетом изменившегося прогнозного фона;

• контроль, заключающийся в оценке полученных результатов прогнозирования и определении эффективности функционирования системы.

Прогностические исследования крупного масштаба начинаются, как правило, с разработки задания на прогноз, т. е. нормативного акта — документа, определяющего объект прогнозирования, его цель, задачи и порядок разработки. Задание на прогноз — это основание для разработки прогноза. Оно составляется с участием заказчика и исполнителя. В случае значительного количества исполнителей может составляться координационный план, утверждаемый заказчиком.

Порядок и последовательность работ как элемент организации прогнозирования определяется в зависимости от основных элементов системы прогнозирования. Обычно эта работа выполняется в несколько этапов.

Первый этап — прогнозная ретроспекция, т. е. установление объекта прогнозирования и прогнозного фона. Работа на первом этапе выполняется в такой последовательности:

• формирование описания объекта в прошлом, что включает пред прогнозный анализ объекта, оценку его параметров, их значимости и взаимных связей;

• определение и оценка источников информации, порядка и организации работы с ними, сбор и размещение ретроспективной информации;

• постановка задач исследования.

Второй этап — прогнозный диагноз. В ходе него исследуется систематизированное описание объекта прогнозирования и прогнозного фона с целью выявления тенденций их развития и выбора моделей и методов прогнозирования. Работа выполняется в такой последовательности:

• разработка модели объекта прогноза, в том числе формализованное описание объекта, проверка степени адекватности модели объекту;

• выбор методов прогнозирования (основного и вспомогательных), разработка алгоритма и рабочих программ.

Третий этап — проспекция, т. е. процесс обширной разработки прогноза, в том числе:

• расчет прогнозируемых параметров на заданный период;

• синтез отдельных составляющих прогноза.

Четвертый этап — оценка прогноза, в том числе его верификация, т. е. определение степени достоверности, точности и обоснованности.

Результаты прогноза оформляются в виде справки, доклада или иного материала и представляются заказчику. В ходе прогнозирования у исполнителей могут возникнуть прогнозный вариант, прогнозная альтернатива и необходимость проверки прогнозного эксперимента.

Прогнозный вариант — это один из прогнозов, составляющих группу взаимоисключающих прогнозов.

Прогнозный эксперимент — это варьирование характеристик объекта прогнозирования на прогнозных моделях с целью выявления возможных, допустимых и недопустимых прогнозных и альтернативных вариантов развития объекта прогнозирования.

Полученные результаты прогнозов могут в дальнейшем корректироваться, т. е. подвергаться уточнению по итогам верификации с учетом дополнительных материалов и исследований. В прогнозировании может быть указана величина отклонения прогноза от действительного состояния объекта, которая называется ошибкой прогноза.

Макро– и микропрогнозирование.

Макроэкономические показатели, отражающие масштабные экономические явления, прогнозируются на уровне государства. Эти прогнозы используются для:

• применения в качестве самостоятельных расчетов;

• планирования, прежде всего бюджетного.

В макроэкономических показателях страны находят отражение параметры функционирования экономики, структура и потенциал ее отраслей, пропорции и взаимосвязи субъектов РФ.

К макроэкономическим показателям, прогнозы которых по заказу правительства страны осуществляет система государственного прогнозирования, относятся:

• валовой внутренний продукт (ВВП);

• объем промышленной продукции;

• объем продукции сельского хозяйства;

• производство потребительских товаров, в том числе продовольственных

и непродовольственных;

• объем розничного товарооборота;

• объем инвестиций (в том числе долговременных материальных

активов);

• эмиссия денег;

• индекс изменения цен, включая и потребительские товары;

• уровень безработицы и др.

Кроме того, к прогнозам макроуровня относятся прогнозные обзоры состояния экономики страны. Их осуществляют не только специальные научные учреждения, но и независимые лица. Варианты прогнозов развития экономики страны часто публикуются в периодической печати. Многообразие альтернатив социально- экономического развития подтверждает факт отсутствия в обществе монополии взглядов на будущее, но одновременно усложняет процедуру выбора одного из вариантов для последующего использования при разработке планов или собственных прогнозов.

Прогнозы макроэкономических показателей, используемых в планировании в качестве базы для обоснования планов государства и регионов, учитываются в расчетах:

• бюджетных планов;

• индикативных планов всей страны и ее регионов;

• планов государственных и муниципальных предприятий, входящих в предпринимательский сектор экономики страны

и пр.

Для получения достоверных прогнозов необходимо знание законов развития общества, особенностей состояния экономики страны, причин и движущих сил развития. Высокая степень неопределенности будущего, особенно в политическом аспекте, обусловливает вероятностный характер достижения параметров макроэкономических прогнозов.

К основным факторам влияния на макроэкономические показатели (объект прогнозирования) относятся (прогнозный фон):

• международная обстановка;

• социальные потребности;

• технические возможности;

• политическое состояние;

• состояние ресурсов;

• экономическая целесообразность.

Результаты макроэкономического прогнозирования используются при решении следующих основных задач:

• установление целей развития:

• изыскание оптимальных путей и средств достижения целей;

• определение потребностей в ресурсах для достижения целей развития. Например, определение доходной части государственного бюджета страны для решения социальных задач общества, определение необходимой суммы инвестиций региону на ближайшие 5—10 лет и т. д.;

• разработка действий различных органов по достижению поставленных целей развития, например действий правительства страны, в том числе Министерства экономики и Министерства финансов, ЦБ РФ, отраслевого министерства и учредителей по оздоровлению убыточной отрасли;

• определение возможных действий противоборствующих

сил и их влияния на решение проблемы, например возможного

воздействия на структуру распределения бюджетных

средств отдельными партиями, олигархами и иными

лоббистами.

На уровне государства задачи экономического предвидения — прогнозирование и планирование — должны рассматриваться взаимосвязано. В процессе разработки прогноза макроэкономического показателя анализируется взаимодействие целей, способов и средств его достижения, а также определяются необходимые ресурсы для реализации. По сути, прогноз на этом уровне приближается к плану.

Несмотря на общность задач, постановка их при прогнозировании и планировании бывает различной (табл.).

Таблица 7.1. Макро- и микропрогнозы

Постановка задачи	Цели	Пути и средства	Ресурсы
Прогноз	Теоретически достижимые	Возможные	Вероятностные
План	Рекомендательные (индикативный план), обязательные (директивный план)	Детерминированные (однозначно достижимые)	Ограниченные

Аналитическое моделирование в прогнозировании.

Простейшие модели, использующие обыкновенные

дифференциальные уравнения

Модель Ланчестера. В простейшей модели борьбы двух противников (скажем, двух армий) — уравнениях Ланчестера (уравнениях динамики боя) — состояние системы описывается точкой (х, у) положительного квадранта плоскости. Здесь рассматривается упрощенная модель (уравнения Ланчестера в общей форме учитывают п р о с т р а н с т в е н н ы й ф а к т о р — расположение.армий на территории, и в конечном итоге должны описывать изменения кривой линии фронта со временем).

Координаты этой точки, х и у — численности противостоящих

армий. Модель имеет вид

Здесь а — мощность оружия армии х, a b — армии у. Попросту говоря, предполагается, что каждый солдат армии х убивает за единицу времени а солдат армии у (и, наоборот, каждый солдат

армии у убивает b солдат армии х). Точка над буквой означает производную по времени, т. е. скорость изменения обозначенной буквой величины.

Это модель, которая позволяет получить решение путем интегрирования

Эволюция численностей армий х и у происходит вдоль гиперболы, заданной этим уравнением. По какой именно гиперболе (/ или 2) пойдет война, зависит от начальной точки.

Эти гиперболы разделены прямой х = y . Если начальная точка лежит выше этой прямой, то гипербола выходит на ось у. Это значит, что в ходе войны численность армии х уменьшается до нуля (за конечное время). Армия у выигрывает, противник уничтожен.

Если начальная точка лежит ниже (кривая 2), то выигрывает армия х.

В разделяющем эти случаи состоянии (на прямой) война заканчивается ко всеобщему удовлетворению истреблением обеих армий. Но на это требуется бесконечно большое время: конфликт продолжает тлеть, когда оба противника уже обессилены.

Вывод модели таков: для борьбы с вдвое более многочисленным противником нужно в 4 раза более мощное оружие, с втрое более многочисленным — в 9 раз и т. д. (на это указывают квадратные корни в уравнении прямой).

Можно думать, что описанная модель отчасти объясняет как неудачи Наполеона и Гитлера, так и успех Батыя и надежды мусульманских фундаменталистов.

Модель Лотка—Вольтерра. Важно, чтобы простейшая модель была структурно устойчивой, т. е. чтобы выводы выдерживали малое изменение параметров и функций, описывающих модель. Описанная выше модель обладает этим свойством структурной устойчивости.

Модели экспоненциального и логистического роста. Простейшее дифференциальное уравнение экспоненциального роста: x = kx

хорошо известно (например, оно было предложена Мальтусом для описания роста численности населения Земли). В результате интегрирования получаем:

Эта модель применима, например, к развитию мировой науки в 1700—1950 гг. (измеряемому числом публикаций или научных работников)

Логистическая модель с внешним воздействием. Логистическая модель является обычной в экологии. Можно себе представить, например, что х — это количество рыб в озере или в мировом океане. Посмотрим теперь, как скажется на судьбе этих рыб рыболовство с интенсивностью (квота вылова) с: x = x-x²-c

Интегрирование показывает, что ответ чувствительно зависит от значения квоты вылова (с). Для рассматриваемой модели это критическое значение есть с = '/4, но аналогичные явления имеют место и для общей модели

x = k(x)x -c

(критическое значение с в этом случае — максимум функции к(х)х).

Проектирование устойчивой динамической системы. Рассмотренная простая модель позволяет, однако, указать способ борьбы с неустойчивостью. Оказывается, устойчивость восстанавливается, если заменить жесткое планирование гибкой обратной связью. Иными словами, решение о величине эксплуатации (квоты вылова, налогового пресса и т. д.) следует принимать не директивно (с = const), а в зависимости от достигнутого состояния системы: c = kx

где параметр к («коэффициент квоты») подлежит выбору.

В этом случае модель принимает вид:

x = x-x²-kx =x(1-x) - x²

Предмет и задачи теории игр.

При изучении процессов принятия решений несколькими субъектами, интересы которых могут не совпадать. При этом возникают задачи со многими целевыми функциями (критериями). Область математики, изучающая данные проблемы, получила название теории игр. Задачи теории игр относятся к области принятия решений в условиях неопределенности, а их специфика состоит в том, что, как правило, подразумевается неопределенность, возникающая в результате действий двух или более «разумных» противников, способных оптимизировать свое поведение за счет других. Среди типичных примеров такого поведения могут быть названы действия конкурирующих фирм на одном рынке или планирование военных операций.

Одним из основных вопросов в задачах с коллективным выбором решений является вопрос об определении оптимальности, т. е. вопрос, какие решения следует признавать наилучшими в ситуации оптимизации по нескольким критериям, отражающим различные интересы. Многие методы решения проблем теории игр основываются на сведении их к задачам математического программирования. На наиболее простых из них мы остановимся в настоящей главе.

- Теория игр берет начало от работ Э. Бореля (1921 г.), а принципиальным этапом в ее становлении как самостоятельного научного направления стала монография Дж. Неймана, вышедшая в 1944 г.

Теория игр — раздел, изучающий математические модели конфликтных ситуаций (т. с. ситуаций, при которых интересы участников либо противоположны и тогда эти модели называются «антагонистическими играми», либо не совпадают, хотя и не противоположны, и тогда речь идет об «играх с не противоположными интересами».) Основоположники теории Дж. фон Нейман и О. Моргенштерн попытались математически описать явления конкуренции как некую «игру». В наиболее простом случае речь идет о противоборстве только двух противников, например двух конкурентов, борющихся за рынок Сбыта. В более сложных случаях в игре участвуют многие, причем они могут вступать между собой в постоянные или временные коалиции, союзы. Игра двух лиц называется парной; когда в ней участвуют п игроков, это «игра п лиц», в случае образования коалиций игра называется «коалиционной».

Суть игры в том, что каждый из участников принимает такие решения (т. е. выбирает стратегии действий), которые, как он полагает, обеспечивают ему наибольший выигрыш или наименьший проигрыш, причем этому участнику игры ясно, что результат зависит не только от него, но и от действий партнера (или партнеров), иными словами, он принимает решения в условиях неопределенности. Эти решения отражаются в таблице, которая называется платежной матрицей. Часто обнаруживается такая точка («седловая»), в которой достигается равновесие, приемлемое для партнеров.

Чисто математическая и потому весьма абстрактная теория игр, разумеется, далеко не полно отражает сложные процессы, происходящие в экономике, однако теоретическое и практическое ее значение намного шире.

Принципиальным достоинством теории игр считают то, что она расширяет общепринятое понятие оптимальности, включая в него такие важные элементы, как, например, компромиссное решение, устраивающее разные стороны в подобном споре (игре). Кроме того, математические приемы теории игр могут применяться для решения многочисленных практических экономических задач на промышленных предприятиях. Например, для выбора оптимальных решений в области повышения качества продукции или определения запасов. «Противоборство» здесь происходит в первом случае между стремлением выпустить больше продукции (затратить на нее меньше труда) и сделать ее лучше, т. е. затратить больше труда, во втором случае — между желанием запасти ресурсов побольше, чтобы быть застрахованным от случайностей, и запасти поменьше, чтобы не замораживать средства.

Следует отметить, что подобные задачи решаются и другими способами. И это не случайно — многие задачи теории игр могут быть сведены, например, к задачам линейного программирования, и наоборот.

Основные понятия теории игр.

Терминология и классификация игр. Особенностью теории игр как научной дисциплины стала употребляемая в ней специфическая терминология. Термин «игра» применяется для обозначения совокупности правил и соглашений, которыми руководствуются субъекты, поведение которых мы изучаем. Каждый такой субъект k, где k  1: К, или игрок, характеризуется наличием индивидуальной системы целевых установок и стратегий ,т. е. возможных вариантов действий в игре.

Достаточно распространенный способ математического описания игры основан на задании функций , каждая из которых определяет результат (платеж, выигрыш), получаемый k-м игроком в зависимости от набора стратегий , примененного всеми участниками игры. Функции f_k,k1:K также называют функциями выигрыша, или платежными функциями. В том случае, если для любых S

игра называется игрой с нулевой суммой. Игру с двумя участниками и нулевой суммой называют антагонистической. Антагонистические игры, т. е. игры, в которых выигрыш одного участника равен проигрышу другого, в силу относительно простой постановки задачи являются наиболее изученным разделом теории игр. Однако содержание теории игр, безусловно, не исчерпывается ими. В классификации игровых моделей выделяют игры с конечными и бесконечными наборами стратегий у игроков, выделяют игры по возможным количествам ходов у участников. Также игры делят на некооперативные и кооперативные, т. е. те, в которых функции выигрыша участников зависят от образуемых ими коалиций. Помимо этого игры можно различать по объему информации, имеющейся у игроков относительно прошлых ходов. В этой связи они делятся на игры с полной и неполной информацией.

Стороны, участвующие в игре (конфликте), называются игроками. В спортивной игре игроками могут быть отдельные лица или команды; в военном конфликте – воюющие стороны; в хозяйственной жизни – предприятия, фирмы.

Иногда под игроком понимается природа, формирующая условия, в которых необходимо принимать решения.

Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от ситуации, сложившейся в процессе игры.

Игра называется конечной, если число стратегий игроков конечно, и бесконечной, если хотя бы у одного из игроков число стратегий является бесконечным.

Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний проигрыш, независимо от поведения противника.

Выбор одной из предусмотренных правилами игры стратегий и ее осуществлением называется ходом. Ходы бывают личные и случайные. Ход называется личным, если игрок сознательно выбирает один из возможных вариантов действий и осуществляет его ( ход в шахматах). Ход называется случайным, если выбор производится не игроком, а каким-либо механизмом случайного выбора (бросание игральной кости или монеты).

Для того, чтобы решить игру, или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности.

Существуют 2 способа описания игр: позиционный и нормальный. Позиционный способ сводится к графу последовательных шагов. Нормальный заключается в явном представлении совокупности стратегий игроков и платежной функции. Платежная функция в игре определяет для каждой совокупности выбранных игроками стратегий выигрыш каждой из сторон. Если в парной игре выигрыш одного игрока равен проигрышу 2^го, то такую игру принято называть игрой с нулевой суммой. Парную игру с нулевой суммой удобно исследовать, если она описана в виде платежной матрицы.

Рассмотрим конечную игру 2^х лиц (I и II) с нулевой суммой. Предположим, что игрок I имеет m стратегий (обозначим их А_1, А_2, …А_n), а игрок II (противник) – n стратегий (В_1, В_2,…В_n). Такая игра называется игрой размерности mxn.

Пусть игрок I выбрал одну из своих возможных стратегий А_i, I=1,2,3,…,m, а игрок II, не зная результата выбора игрока I, выбрал стратегию В_j, j=1,2,3,…,n. Выигрыш игрока I W₁(A_i,B_j) и игрока II W₂(A_i_,B_j) в результате выбора стратегий удовлетворяет соотношение W₁(A_i,B_j)+ W₂(A_i_,B_j)=0. Если положить W₁(A_i,B_j)= W(A_i_,B_j), тогда имеем: W₂(A_i_,B_j)= - W(A_i_,B_j)

Пусть W(A_i_,B_j)=а_ij_.Предположим, что значения а_ijнам известны при каждой паре стратегий. Запишем эти значения в виде таблицы: строке которой соответствуют стратегиям игрока I, а столбцы – стратегиям игрока II. Такая таблица называется платежной матрицей.

II I	B1	B2	_…_._..	Bn
A₁	а₁₁	а₁₂	……	а_1n
A₂	а₂₁	а₂₂	……	а₂_n
……	……	……	.…..	……
A_m	а_m1	а_m2	……	а_mn

Каждый положительный элемент а_ijматрицы определяет величину выигрыша игрока I и проигрыша игрока II при применении ими соответствующих стратегий. Цель игрока I – максимизировать свой выигрыш, а игрока II – минимизировать свой проигрыш.

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.20162.08 Mб454организ.- произв. структ. тр-та.doc
#
16.02.20162.09 Mб353организ.- произв. структ. тр-та.doc
#
16.02.20161.21 Mб145осбен.уголовное.doc
#
16.02.2016439.81 Кб47Основы маркетинга.doc
#
16.02.2016266.95 Кб74Ответы еще_Экономическая теория.pdf
#
10.11.20192.79 Mб35Ответы Мат Методы.doc
#
16.02.2016162.06 Кб244ответы на Госы по ТГП.docx
#
16.02.2016286.21 Кб39Ответы на ПРАВО.doc
#
16.02.201689.6 Кб367ОТВЕТЫ Общий тестя.doc
#
16.02.201695.23 Кб249ОТВЕТЫ ТЕСТ ЭКОНОМИКЕ.doc
#
16.02.201624.3 Кб37Отзыв НР (с компетенциями).docx

х
1	0,2	1,0	2,1	0
2	0,9	1,1	2,5	2,0
3	1,0	1,3	2,9	2,5
4	1,2	1,4	3,9	3,0
5	2,0	1,8	4,9	4,0

х
1	0,2	1,0	2,1	0
2	0,9	1,1	2,5	2,0
3	1,0	1,3	2,9	2,5
4	1,2	1,4	3,9	3,0
5	2,0	1,8	4,9	4,0

х
1	0,2	1,0	2,1	0
2	0,9	1,1	2,5	2,0
3	1,0	1,3	2,9	2,5
4	1,2	1,4	3,9	3,0
5	2,0	1,8	4,9	4,0