1. Постановка задачи.

2. Построение содержательной (вербальной) модели рас­сматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возмож­ных управляющих воздействий, влияющих на достижение сфор­мулированной цели, а также описание системы ограничений на управляющие воздействия. \

3. Построение математической модели, т. е. перевод сконст­руированной вербальной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

4. Решение задач, сформулированных на базе постро­енной математической модели.

5. Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная коррек­тировка первоначальной модели.

6. Реализация полученного решения на практике.

Центральное место в данной книге отведено вопросам, отно­сящимся к четвертому пункту приведенной выше схемы. Это делается не потому, что он является самым важным, сложным или интересным, а потому, что остальные пункты существенно зависят от конкретной природы изучаемой системы, в силу чего для действий, которые должны производиться в их рамках, не могут быть сформулированы универсальные и содержательные рекомендации. По этому поводу, например, X. Таха заметил, что исследование операций одновременно является как наукой, так и искусством [27].

Математическое моделирование в исследовании операций является, с одной стороны, очень важным и сложным, а с дру­гой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся по­пытки выделить общие принципы создания математических мо­делей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкрет­ных проблем, либо, наоборот, к появлению рецептов, примени­мых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой мате­матического моделирования на конкретных примерах.

В качестве таких примеров приведем несколько классиче­ских экономико-математических моделей и задач, которые мо­гут быть сформулированы на их основе.

Управление портфелем активов. Рассмотрим проблему принятия инвестором решения о вложении имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные имена от А до F, задается следующей таблицей.

Название	Доходность (в %)	Срок выкупа (год)	Надежность (в баллах)
А	5,5	2001	5
В	6,0	2005	4
С	8,0	2010	2
D	7,5	2002	3
Е	5,5	2000	5
F	7,0	2003	4

Предположим, что при принятии решения о приобретении активов должны быть соблюдены условия:

1. суммарный объем капитала, который должен быть вложен, составляет $ 100 000;

2. доля средств, вложенная в один объект, не может превы­шать четверти от всего объема;

3. более половины всех средств должны быть вложены в дол­госрочные активы (допустим, на рассматриваемый момент к тако­вым относятся активы со сроком погашения после 2004 г.);

4. доля активов, имеющих надежность менее чем 4 балла, не может превышать трети от суммарного объема.

Приступим к составлению экономико-математической моде­ли для данной ситуации. Целесообразно начать процесс с опре­деления структуры управляемых переменных. В рассматривае­мом примере в качестве таких переменных выступают объемы средств, вложенные в активы той или иной фирмы. Обозначим их как х_А, х_В, х_С, х_D, х_E, х_F. Тогда суммарная прибыль от раз­мещенных активов, которую получит инвестор, может быть представлена в виде

(1)

На следующем этапе моделирования мы должны формально описать перечисленные выше ограничения a-d на структуру портфеля.

a) Ограничение на суммарный объем активов:

x_A + x_B + x_С + x_D + x_E + x_F  100 000 . (2)

b) Ограничение на размер доли каждого актива:

х_А  25 000, х_В  25 000, х_С  25 000,

x_d  25 000, х_е  25 000, x_f  25 000. (3)

c) Ограничение, связанное с необходимостью вкладывать по­ловину средств в долгосрочные активы:

х_В + х_С  50 000 (4)

d) Ограничение на долю ненадежных активов:

x_C + x_D  30 000. (5)

Наконец, система ограничений в соответствии с экономиче­ским смыслом задачи должна быть дополнена условиями неот­рицательности для искомых переменных:

х_А  0, х_B  0, х_C  0, x_D  0, х_Е  0, x_F  0. (6)

Выражения (1)-(6) образуют математическую модель поведения инвестора. В рамках этой модели может быть по­ставлена задача поиска таких значений переменных х_а, х_B, х_C, x_d, x_e, х_F, при которых достигается наибольшее значение при­были (т. е. функции (1)) и одновременно выполняются ограни­чения на структуру портфеля активов (2)-(6).

Перейдем теперь к рассмотрению более общих моделей и задач.

8. Общий вид задач линейного программирования.

В общем виде задача линейного программирования (в дальней­шем ЗЛП) может быть сформулирована как задача нахождения наибольшего значения линейной функции

(1.1)

на некотором множестве D  Rⁿ ,где x  D удовлетворяют сис­теме ограничений

(1.2)

и, возможно, ограничениям

(1.3)

He умаляя общности, можно считать, что в системе (1.2) пер­вые т ограничений являются неравенствами, а последующие — l-уравнениями. Очевидно, этого всегда можно добиться за счет простого переупорядочения ограничений. Относительно направ­ления знака неравенства будем предполагать, что левая часть меньше или равна правой. Добиться этого можно, умножив на (-1) обе части тех неравенств, которые имеют противопо­ложный знак. Ограничения (1.3), вообще говоря, могут быть рассмотрены как частный случай ограничений в форме нера­венств, но в силу особой структуры их обычно выделяют от­дельно и называют условиями неотрицательности (или три­виальными ограничениями).

Дополнительно следует заметить, что выбор типа искомого экстремума (максимума или минимума) также носит относитель­ный характер. Так, задача поиска максимума функции

(1.4)

эквивалентна задаче поиска минимума функции

(1.5)

Часто условия задачи (1.1) - (1.3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращен­ной матричной форме

(1.6)

где с и x — векторы из пространства Rⁿ, b — вектор из простран­ства R^m, a А — матрица размерности m  п.

Задачу линейного программирования, записанную в форме (1.1) - (1.3), называют общей задачей линейного програм­мирования (ОЗЛП).

9. Основная задача линейного программирования, ее формы.

Формы задачи линейного программирования.

Задачей линейного программирования (ЗЛП) называется такая задача математического программирования, в которой:

1. D – множество точек (векторов) в арифметическом линейном пространстве Rⁿ , заданное системой линейных ограничений (уравнений и нестрогих неравенств);

2. Функция f – линейна

Стандартная ЗЛП

ЗЛП называется стандартной, если ограничения имеют вид неравенств, и на все переменные x_i наложены условия неотрицательности x_i 0_.

Каноническая ЗЛП

ЗЛП называется канонической, если на все переменные наложены условия неотрицательности, а все остальные ограничения имеют вид уравнений.

Общая ЗЛП

Если ЗЛП не может быть отнесена ни к классу стандартных, ни к классу канонических задач, она называется общей ЗЛП.

В общем виде задача линейного программирования может быть сформулирована как задача нахождения наибольшего значения линейной функции

(1.1)

на некотором множестве D  Rⁿ ,где x  D удовлетворяют сис­теме ограничений

(1.2)

и, возможно, ограничениям

(1.3)

He умаляя общности, можно считать, что в системе (1.2) пер­вые т ограничений являются неравенствами, а последующие — l-уравнениями. Очевидно, этого всегда можно добиться за счет простого переупорядочения ограничений. Относительно направ­ления знака неравенства будем предполагать, что левая часть меньше или равна правой. Добиться этого можно, умножив на (-1) обе части тех неравенств, которые имеют противопо­ложный знак. Ограничения (1.3), вообще говоря, могут быть рассмотрены как частный случай ограничений в форме нера­венств, но в силу особой структуры их обычно выделяют от­дельно и называют условиями неотрицательности (или три­виальными ограничениями).

Дополнительно следует заметить, что выбор типа искомого экстремума (максимума или минимума) также носит относитель­ный характер. Так, задача поиска максимума функции

(1.4)

эквивалентна задаче поиска минимума функции

(1.5)

Часто условия задачи (1.1) - (1.3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращен­ной матричной форме

(1.6)

где с и x — векторы из пространства Rⁿ, b — вектор из простран­ства R^m, a А — матрица размерности m  п.

Задачу линейного программирования, записанную в форме (1.1) - (1.3), называют общей задачей линейного програм­мирования (ОЗЛП).

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные x_j наложены усло­вия неотрицательности, то она называется задачей линейного программирования в канонической форме, или канонической задачей линейного программирования (КЗЛП). В матрич­ной форме КЗЛП можно записать в следующем виде:

(1.7)

Поскольку любая оптимизационная задача однозначно оп­ределяется целевой функцией f и областью D, на которой отыс­кивается оптимум (максимум), будем обозначать эту задачу парой (D, f).

Условимся относительно терминологии, которая использу­ется в дальнейшем и является общепринятой в теории линейно­го программирования.

Планом ЗЛП называется всякий вектор х из пространства Rⁿ.

Допустимым планом называется такой план ЗЛП, кото­рый удовлетворяет ограничениям (1.2)-(1.3), т. е. содержится в области D. Сама область D называется при этом областью допустимых планов. Оптимальным планом х^* называется такой допустимый план, при котором целевая функция достига­ет оптимального (в нашем случае — максимального) значения, т. е. план, удовлетворяющий условию

max f(x) = f(x^*).

Величина f^* = f(x^*) называется оптимальным значением целевой функции.

Решением задачи называется пара (х^*, f^*), состоящая из оптимального плана и оптимального значения целевой функ­ции, а процесс решения заключается в отыскании множества всех решений ЗЛП.

Переход к канонической форме. Подавляющее боль­шинство известных методов решения задач линейного програм­мирования предназначены для канонических задач. Поэтому начальный этап решения всякой общей задачи линейного программирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста:

• ограничения в виде неравенств преобразуются в уравне­ния за счет добавления фиктивных неотрицательных переменных , которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение;

• переменные, на которые не наложено условие неотрица­тельности, представляются в виде разности двух новых неотрицательных переменных:

Проиллюстрируем применение описанных выше рекоменда­ций на примере. Пусть задана задача линейного программирова­ния (D, f) в общей форме с целевой функцией

и множеством допустимых планов D, определенным системой уравнений и неравенств,

Тогда в соответствии со сформулированными правилами эк­вивалентная каноническая задача будет иметь вид , где:

а множество определено как:

Нетрудно заметить, что «платой» за переход от общей фор­мы задачи линейного программирования к канонической явля­ется рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.

10. Сведение произвольной задачи линейного программирования к основной задаче линейного программирования.

Как можно перейти от задачи с ограничениями- неравенствами к основной задаче линейного программирования.

Пусть имеется задача линейного программирования с п переменными х₁ х₂, ..., х_n„ в которой ограничения, наложенные на переменные, имеют вид линейных неравенств. В некоторых из них знак неравенства может быть , а других (второй вид сводится к первому переменой знака обеих частей). Поэтому зададим все ограничения-неравенства в стандартной форме:

(1)

Будем считать, что все эти неравенства л и н е й н о независимы (т. е. никакое из них нельзя представить в виде линейной комбинации других).

Требуется найти такую совокупность неотрицательных значений х₁, х₂, ..., х_п, которая удовлетворяла бы неравенствам (1), и, кроме того, обращала бы в минимум линейную функцию: (2) От поставленной таким образом задачи легко перейти к основной задаче линейного программирования. Действительно, введем новые («дополнительные») переменные у₁, у₂, ..., у_m как: (3)

(3)

Согласно условиям (1), эти дополнительные переменные так же, как и х₁, х₂, ..., х_п должны быть неотрицательными. Таким образом, может быть сформулирована следующая задача линейного программирования: найти такие неотрицательные значения п + т переменных х₁, х₂, ..., х_п у₁, у₂, ..., у_m, чтобы они удовлетворяли системе уравнений (3) и одновременно обращалив минимум линейную функцию этих переменных (2).

Как видно, перед нами основная задача линейного программирования (03). Уравнения (3) заданы в форме, разрешенной относительно базисных переменных у₁, у₂, ..., у_m, которые выражены через свободные переменные х₁, х₂, ..., х_п. Общее количество переменных равно п + т, из них п «основные» и т «дополнительные». Функция F выражена только через исходные переменные (коэффициенты при «дополнительных» переменных в ней равны нулю).

Таким образом, задача линейного программирования с ограничениями-неравенствами сведена нами к основной задаче линейного программирования, но с большим числом переменных, чем первоначально было в задаче.

Аналогично, всегда можно осуществить обратный переход — от ОЗ к задаче с неравенствами, для этого необходимо уменьшить число переменных, устраняя базисные и оставляя толькосвободные.

11. Основные теоремы линейного программирования.

Рассмотрим некоторые теоремы, отражающие фундамен­тальные свойства задач линейного программирования и лежа­щие в основе методов их решения. Они по существу обобщают на случай задач с произвольным количеством переменных те свойства, которые мы наблюдали в двумерном случае.

Теорема 1.1. Если целевая функция f принимает мак­симальное значение в некоторой точке множества до­пустимых планов D, то она принимает это значение и в некоторой угловой точке данного множества.

Доказательство.

Чтобы не усложнять изложение, ограничимся тем случаем, когда множество D ограничено, и, следовательно, является вы­пуклым многогранником.

Для доказательства воспользуемся следующим известным свойством ограниченных выпуклых множеств:

Если D — замкнутое ограниченное выпуклое множе­ство, имеющее конечное число угловых точек, то лю­бая точка x&D может быть представлена в виде вы­пуклой комбинации угловых точек D.

Строгое доказательство данного утверждения см., например, в [14].

Пусть х¹, х²,..., х^т — угловые точки множества D, а х^* — точка, в которой целевая функция f достигает максимума.

На основе сформулированного выше утверждения точку х^* можно представить в виде выпуклой комбинации угловых точек х¹, х²,..., х^т

где

Так как х^* — точка максимума, то для любого х  D сх^*  сх. Функция f(x) — линейная, поэтому

следовательно,

(1.10)

где х^r — угловая точка, удовлетворяющая условию

Из (1.10) видно, что сх^*  сх^r. В то же время справедливо об­ратное неравенство: сх^*  сх^r. Откуда следует, что сх^* = сх^r, т. е. существует по крайней мере одна угловая точка x^r, в которой целевая функция принимает максимальное значение. ▲

Теорема 1.2. Если целевая функция f принимает мак­симальное значение в нескольких точках множества D, то она принимает это же значение в любой точке, яв­ляющейся их выпуклой комбинацией.

Доказательство.

Пусть максимальное значение функции f достигается в точ­ках ,т. е. . Рассмотрим произвольную выпуклую комбинацию этих точек

где (1.11)

Найдем значение целевой функции в точке х^*

(1.12)

Итак, для произвольной выпуклой комбинации х^* точек справедливо равенство

f(x^*)=cx^*=f^* ▲ (1.13)

Теорема 1.3. Каждый допустимый базисный план яв­ляется угловой точкой множества допустимых пла­нов D.

12. Каноническая форма задачи линейного программирования.

ЗЛП называется канонической, если на все переменные наложены условия неотрицательности, а все остальные ограничения имеют вид уравнений.

Подавляющее боль­шинство известных методов решения задач линейного програм­мирования предназначены для канонических задач. Поэтому начальный этап решения всякой общей задачи линейного программирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста:

• ограничения в виде неравенств преобразуются в уравне­ния за счет добавления фиктивных неотрицательных переменных , которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение;

• переменные, на которые не наложено условие неотрица­тельности, представляются в виде разности двух новых неотрицательных переменных:

Проиллюстрируем применение описанных выше рекоменда­ций на примере. Пусть задана задача линейного программирова­ния (D, f) в общей форме с целевой функцией

и множеством допустимых планов D, определенным системой уравнений и неравенств,

Тогда в соответствии со сформулированными правилами эк­вивалентная каноническая задача будет иметь вид , где:

а множество определено как:

Нетрудно заметить, что «платой» за переход от общей фор­мы задачи линейного программирования к канонической явля­ется рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.

13. Сведение общей задачи линейного программирования к каноническому виду.

ЗЛП называется канонической, если на все переменные наложены условия неотрицательности, а все остальные ограничения имеют вид уравнений.

Подавляющее боль­шинство известных методов решения задач линейного програм­мирования предназначены для канонических задач. Поэтому начальный этап решения всякой общей задачи линейного программирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста:

• ограничения в виде неравенств преобразуются в уравне­ния за счет добавления фиктивных неотрицательных переменных , которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение;

• переменные, на которые не наложено условие неотрица­тельности, представляются в виде разности двух новых неотрицательных переменных:

Проиллюстрируем применение описанных выше рекоменда­ций на примере. Пусть задана задача линейного программирова­ния (D, f) в общей форме с целевой функцией

и множеством допустимых планов D, определенным системой уравнений и неравенств,

Тогда в соответствии со сформулированными правилами эк­вивалентная каноническая задача будет иметь вид , где:

а множество определено как:

Нетрудно заметить, что «платой» за переход от общей фор­мы задачи линейного программирования к канонической явля­ется рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.

14. Графический метод решения задач линейного программирования.

Графический метод используется для решения задач с двумя переменными следующего вида:

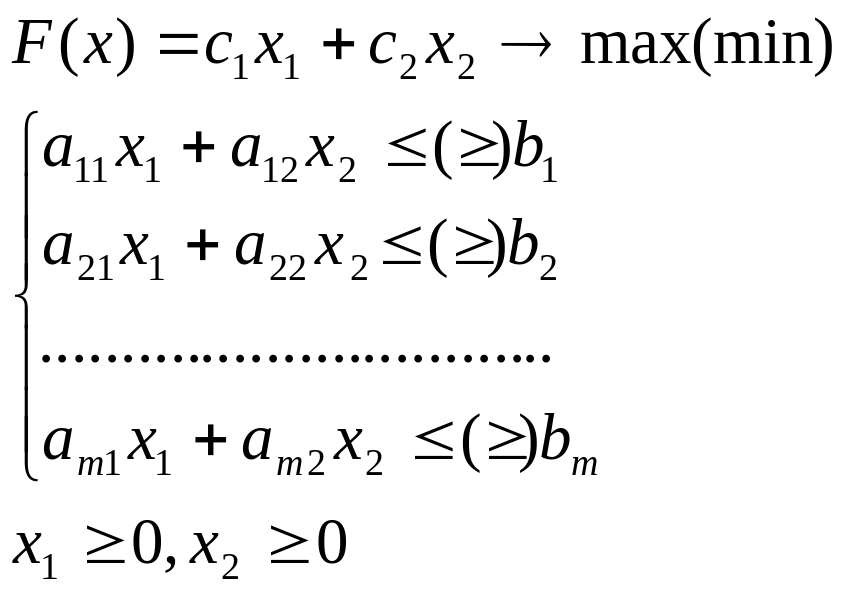
Данный метод основан на возможности графического изображения области допустимых решений задачи и нахождении среди них оптимального решения.

Область допустимых решений задачи строится как пересечение (общая часть) областей решений каждого из заданных ограничений.

Областью решений линейного неравенства является одна из двух полуплоскостей, на которые прямая ,соответствующая данному неравенству, делит всю координатную плоскость.

Для того, чтобы определить какая из двух координатных полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.

Областью допустимых решений задачи является общая часть полуплоскостей – областей решений всех неравенств системы ограничений.

Для нахождения среди допустимых решений оптимального решения используют линии уровня и опорные прямые.

Л инией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в общем случае имеет вид . Все линии уровня параллельны между собой. Их нормаль n = (c₁,с₂).

Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.

Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.

Значение целевой функции на линиях уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.

Алгоритм графического метода решения задач линейного программирования с двумя переменными:

1. Построить область допустимых решений

2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместимости системы ограничений.

3. Е сли область допустимых решений является не пустым множеством, построить нормаль линий уровня n = (c₁,с₂) и одну из линий уровня, имеющую общие точки с этой областью.

4. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном направлении.

5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.

6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.

15. Симплекс-метод решения задач линейного программирования.

Симплексом в n-мерном пространстве называют фигуру, содержащую n+1 вершину. На плоскости – это треугольник, в трехмерном пространстве – тетраэдр и т.д.

Симплекс-метод представляет собой направленный перебор угловых точек допустимого множества решений в сторону приближения к искомой точке экстремума.

Опорным решением задачи линейного программирования называется такое допустимое решение, для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений), соответствующие положительным координатам линейно независимы.

Базисом опорного решения называется базис системы векторов условий задачи, включающий в свой состав векторы, соответствующие отличным от нуля координатам опорного решения.

Канонический вид:

Алгоритм составления симплексных таблиц:

Для определенности будем считать, что решается задача на отыскание максимума.

1. Записать расширенную систему задачи. Она включает в себя систему ограничений и целевую функцию, приведенные к каноническому виду.

Предполагается, что все добавочные переменные имеют тот же знак, что и свободные члены.