
Отношения и функции
79.
Пусть
![]() .
Изобразить R1
и R2
графически, проверить, является ли
отношение R2
рефлексивным, симметричным, транзитивным.
Найти матрицу отношения
.
Изобразить R1
и R2
графически, проверить, является ли
отношение R2
рефлексивным, симметричным, транзитивным.
Найти матрицу отношения
![]() .
.
а)
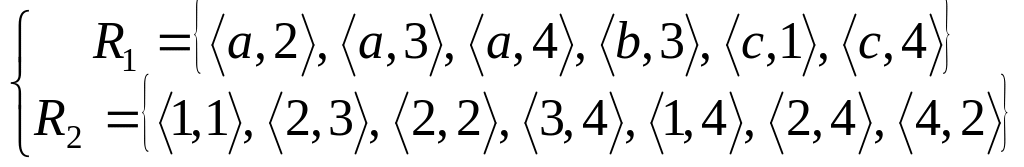 ;
;
б)
 .
.
80. Найти область определения, область значений отношения R. Является ли отношение R рефлексивным, симметричным, транзитивным?
а)
![]() ;
;
б)
![]() .
.
81.
Пусть множество
![]() задает клетки шахматной доски. Опишите
следующие бинарные отношения на S:
задает клетки шахматной доски. Опишите
следующие бинарные отношения на S:
![]() ;
;
![]() .
Будут ли эти отношения эквивалентностями?
Опишите отношение
.
Будут ли эти отношения эквивалентностями?
Опишите отношение
![]() .
.
82.
Найти
![]() для следующих отношений, установить их
свойства: а)
для следующих отношений, установить их
свойства: а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() ;
;
г) ![]() .
.
83.
Сотрудниками фирмы являются генеральный
директор, главный инженер, главный
бухгалтер, начальник цеха, кассир,
рабочий. Построить матрицу бинарного
отношения R
– «начальник – подчиненный». Найти
обратное отношение и композицию
![]() .
.
84. Два бетонных завода получают песок из одного карьера и поставляют конструкции на три ДСК. Построить матрицу бинарного отношения R – «поставщик – потребитель». Найти обратное отношение и композицию .
85.
Бинарные отношения R1,
R2
заданы своими матрицами:
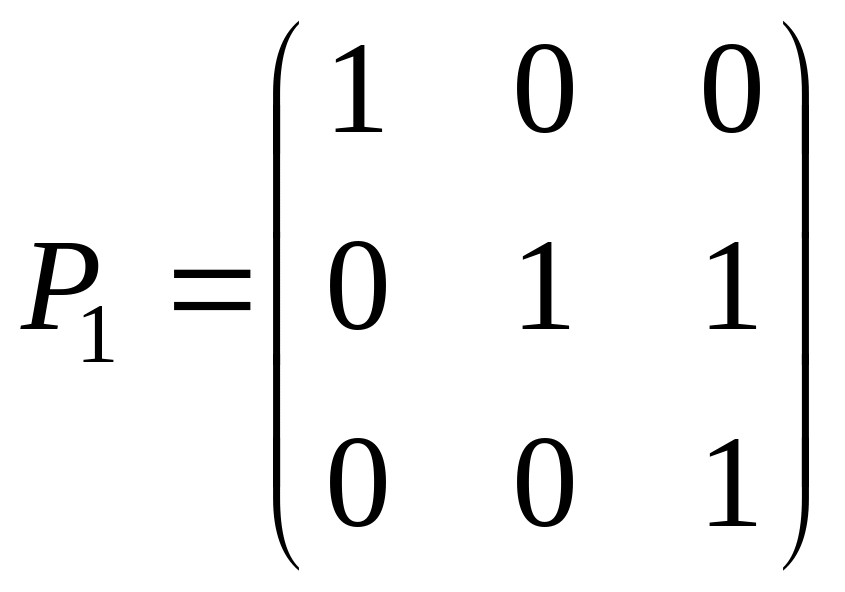 ,
,
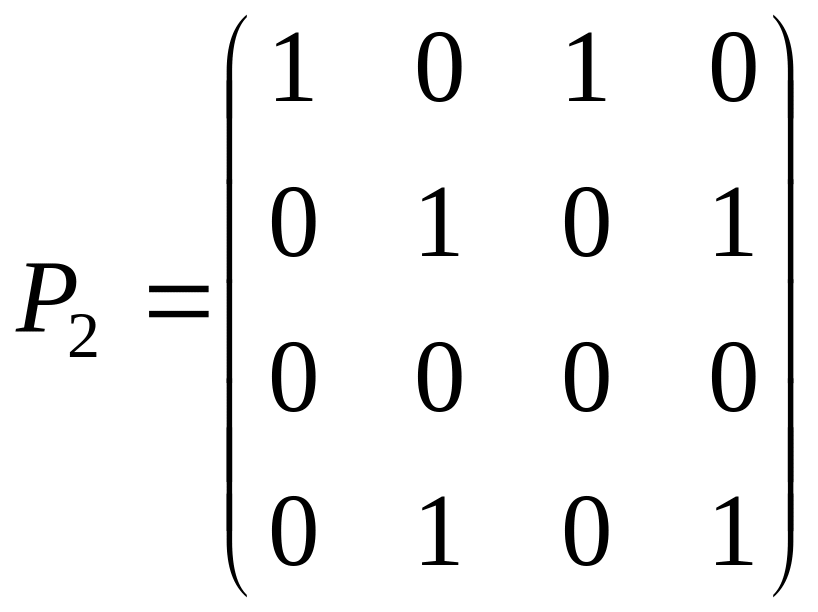 .
Какими свойствами они обладают? Постройте
графы, изображающие эти отношения.
.
Какими свойствами они обладают? Постройте
графы, изображающие эти отношения.
86.
Пусть на множестве
![]() определено
отношение R.
Построить матрицу отношения, указать
его свойства. Задать матрицами отношения
определено
отношение R.
Построить матрицу отношения, указать
его свойства. Задать матрицами отношения
![]() ,
если:
,
если:
1) R «быть меньше»; 2) R «отличаться на 2»; 3) R «иметь общий делитель, отличный от 1».
87.
На множестве A={2,
3, 10, 12, 15} определено бинарное отношение
![]() .
Какими свойствами оно обладает?
.
Какими свойствами оно обладает?
88.
Пусть Х
– непустое множество, на котором задана
функция
![]() .
Отношение R
определено равенством
.
Отношение R
определено равенством
![]() .
Определить свойства этого отношения.
.
Определить свойства этого отношения.
89.
Отношение R
на множестве
![]() задано
матрицей
задано
матрицей
 .
Выполнить унарные операции над ним,
определить свойства исходного и
полученных отношений.
.
Выполнить унарные операции над ним,
определить свойства исходного и
полученных отношений.
90.
Пусть на множестве
![]() отношения R1
и R2
заданы матрицами
отношения R1
и R2
заданы матрицами
 и
и
 соответственно. Выполнить бинарные
операции над отношениями, определить
свойства исходных и полученных отношений.
соответственно. Выполнить бинарные
операции над отношениями, определить
свойства исходных и полученных отношений.
91.
Пусть на множестве А={1,
3, 5, 7} задано отношение R:
![]() .
Определить свойства этого отношения,
выполнить унарные операции над R.
.
Определить свойства этого отношения,
выполнить унарные операции над R.
92.
Пусть А={1,
3, 5, 7} и R
задано на А:
![]() .
Определить свойства этого отношения,
выполнить унарные операции над R.
.
Определить свойства этого отношения,
выполнить унарные операции над R.
93.
Доказать, что для любых бинарных отношений
R,
R1,
R2
справедливы равенства:
![]()
94.
Доказать, что для любой функции f
справедливы включения: а) ![]() ;
б)
;
б)
![]() ;
при каком условии включение можно
заменить равенством? в)
;
при каком условии включение можно
заменить равенством? в)
![]() .
.
95. Пусть П – множество прямых на плоскости. Будут ли эквивалентностями следующие отношения:
- параллельность прямых;
- перпендикулярность прямых?
96.
На множестве целых чисел Z
определено бинарное отношение R:
![]() .
Является ли оно отношением эквивалентности?
.
Является ли оно отношением эквивалентности?
97.
На множестве рациональных чисел Q
определено бинарное отношение R:
![]() .
Является ли оно отношением эквивалентности?
Описать классы эквивалентности,
содержащие числа 1.5; –1; 0.1.
.
Является ли оно отношением эквивалентности?
Описать классы эквивалентности,
содержащие числа 1.5; –1; 0.1.
98.
На множестве NN
рассмотрим отношение R:
![]() .
Доказать, что R
отношение эквивалентности.
.
Доказать, что R
отношение эквивалентности.
99.
На множестве NN
рассмотрим отношение R:
![]() .
Доказать, что R
отношение эквивалентности.
.
Доказать, что R
отношение эквивалентности.
100.
Отношение R
задано на множестве натуральных чисел
N
правилом:
![]() .
Является ли R
отношением порядка?
.
Является ли R
отношением порядка?
101.
Пусть
![]() – произвольный конечный алфавит.
Обозначим через
– произвольный конечный алфавит.
Обозначим через
![]() множество слов длины n
в этом алфавите (словом называется любая
последовательность символов алфавита),
через
множество слов длины n
в этом алфавите (словом называется любая
последовательность символов алфавита),
через
![]() – множество всех слов в алфавите А.
Определим отношение R1
на множестве
.
Пусть
– множество всех слов в алфавите А.
Определим отношение R1
на множестве
.
Пусть
![]() ,
,
![]() ;
тогда
;
тогда
![]() для
всех номеров k
от 1 до n
выполняется
для
всех номеров k
от 1 до n
выполняется
![]() и хотя бы для одного k
имеет место строгое неравенство
и хотя бы для одного k
имеет место строгое неравенство
![]() .
Определим отношение R2
на множестве
.
Пусть
,
.
Определим отношение R2
на множестве
.
Пусть
,
![]() ;
тогда
;
тогда
![]() существует
такое k
в интервале от 1 до n,
что при l<k
выполняется
существует
такое k
в интервале от 1 до n,
что при l<k
выполняется
![]() неравенство
или n<r
и первые n
символов слова v
совпадают со словом u.
Являются ли отношения R1
и R2
отношениями частичного (линейного)
порядка?
неравенство
или n<r
и первые n
символов слова v
совпадают со словом u.
Являются ли отношения R1
и R2
отношениями частичного (линейного)
порядка?
102. Установить взаимно однозначное соответствие между N и Z.
103. Установить взаимно однозначное соответствие между (0, 1) и R.
104. Доказать равномощность множеств [0, 1] и [a, b].
105. Доказать, что отрезок [0, 1] равномощен интервалу (0, 1).
106. Доказать, что мощность булеана множества больше мощности самого множества.
107. Привести пример множества, мощность которого больше с.
