
СБОРНИК ЗАДАЧ
по дисциплине «ДИСКРЕТНАЯ МАТЕМАТИКА – 1 семестр» (2012 г.)
Литература
Основная
1. Новиков Ф.А. Дискретная математика: Учебник для вузов. Стандарт третьего поколения. – СПб.: Питер, 2011. – 384 с.
2. Дехтярь М.И. Лекции по дискретной математике: Учебное пособие. – М.: Интернет-Университет Информационных технологий; БИНОМ. Лаборатория знаний, 2009. – 259 с.
3. Тишин В.В. Дискретная математика в примерах и задачах. – СПб.: БХВ-Петербург, 2008. – 352 с.
Дополнительная
4. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях. – М.: Логос, 2000. – 240 с.
5. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2006. – 400 с.
6. Андерсон Дж. Дискретная математика и комбинаторика. – Издательский дом «Вильямс», 2003. – 960 с.
7. Конышева Л.К., Назаров Д.М. Основы теории нечетких множеств: Учебное пособие. – СПб.: Питер, 2011. – 192 с.
Теория множеств
1.
Даны множества
![]() ,
,
![]() ,
,
![]() .
Найти множества
.
Найти множества
![]() .
.
2.
Даны множества
![]() ,
,
![]() .
Найти множества
.
Найти множества
![]() .
.
3.
Рассмотрим Q
– множество всех рабочих цеха и его
подмножества: K
– квалифицированные рабочие; В
– ветераны цеха; С
– рабочие со средним образованием; Н
– рабочие с неполным средним образованием.
Что означают записи:
![]() ?
Изобразить все множества на диаграмме
Венна.
?
Изобразить все множества на диаграмме
Венна.
4.
Рассмотрим Q
– множество автомашин в гараже и его
подмножества: Л
– легковые автомашины; Г
– грузовые автомашины
![]() ;
О
– отечественные машины; И
– импортные машины; К
– машины красного цвета; Р
– машины на ремонте. Что означают записи:
;
О
– отечественные машины; И
– импортные машины; К
– машины красного цвета; Р
– машины на ремонте. Что означают записи:
![]() ?
Изобразить все множества на диаграмме
Венна.
?
Изобразить все множества на диаграмме
Венна.
5. Старейший математик среди шахматистов и старейший шахматист среди математиков – это один и тот же человек или (возможно) разные? Лучший математик среди шахматистов и лучший шахматист среди математиков – это один и тот же человек или (возможно) разные? Каждый десятый математик – шахматист, а каждый шестой шахматист – математик. Кого больше – математиков или шахматистов – и во сколько раз?
6. Проверить правильность следующих рассуждений: 1) если всех хищников можно приручить и всех львов можно приручить, то все львы – хищники; 2) все следователи – юристы. Некоторые следователи имеют высшее образование. Значит, все юристы имеют высшее образование; 3) все кошки являются рыбами. У всех рыб четыре ноги. Значит, у кошки четыре ноги.
7. Среди 35 туристов только английским языком владеют 11 человек, английским и французским – 5 человек, 9 человек не владеют ни английским, ни французским. Сколько человек владеют только французским языком?
8. Группа из 92 студентов собралась в поход. Из них 47 студентов приготовили бутерброды с колбасой, 38 – с сыром, 42 – с ветчиной. 28 – с колбасой и сыром, 31 – с колбасой и ветчиной, 26 – с сыром и ветчиной. Взяли с собой бутерброды всех трех сортов 25 студентов, а некоторые взяли только по пакету молока. Сколько было таких, которые взяли только молоко?
9. Из 220 студентов 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и футбол?
10. Пусть множество AN и каждый элемент А есть число, кратное или 2, или 3, или 5. Найти число элементов множества А, если среди них имеется: 70 чисел, кратных 2; 60 чисел, кратных 3; 80 чисел, кратных 5; 32 числа, кратных 6; 35 чисел, кратных 10; 38 чисел, кратных 15; 20 чисел, кратных 30.
11. Все участники туристической поездки владеют, по крайней мере, одним иностранным языком. 6 из них владеют английским языком, 6 – немецким, 7 – французским, 4 – английским и немецким, 3 – немецким и французским, 2 – французским и английским, 1 турист владеет английским, французским и немецким. Сколько туристов в группе?
12. Из 100 опрошенных студентов 50 изучают химию, 53 – математику, 42 – физику, 15 – химию и физику, 20 – физику и математику, 25 – математику и химию, 5 студентов изучают все три предмета. Сколько студентов изучают хотя бы один из перечисленных предметов?
13.
Даны множества
![]() .
Построить их на числовой прямой и найти
множества АВ,
А\B,
B\A,
AB,
АВ.
.
Построить их на числовой прямой и найти
множества АВ,
А\B,
B\A,
AB,
АВ.
14.
Построить на числовой прямой множество,
заданное системой неравенств:
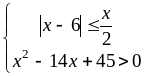 .
.
15.
Построить на числовой плоскости множества
А=![]() ,
В=
,
В=![]() .
Найти АВ,
А\B,
B\A,
AB,
АВ.
.
Найти АВ,
А\B,
B\A,
AB,
АВ.
16.
Построить на числовой плоскости множества
![]() ,
,
![]() .
Найти АВ,
А\B,
B\A,
AB,
АВ.
.
Найти АВ,
А\B,
B\A,
AB,
АВ.
17.
Построить на числовой плоскости множества
![]() ,
,
![]() ,
,
![]() .
Найти множество
.
Найти множество
![]() .
.
