Раздел 1. Элементы линейной алгебры

Тема 1.1. Матрицы и определители Задание 3. Нахождение определителей п-го порядка, миноров и алгебраических дополнений – 1 ч.

Цель: формирование умения находить определители второго, третьего и четвертого порядка, вычислять миноры и алгебраические дополнения элементов определителя.

Задание для самостоятельной внеаудиторной работы:

 3.1. Запомните, какова методика нахождения определителей второго, третьего и четвертого порядка. Выучите, что называют минорами и алгебраическими дополнениями элементов определителя.

3.2. Вычислите определитель:

_{а) ; б) ; в) .}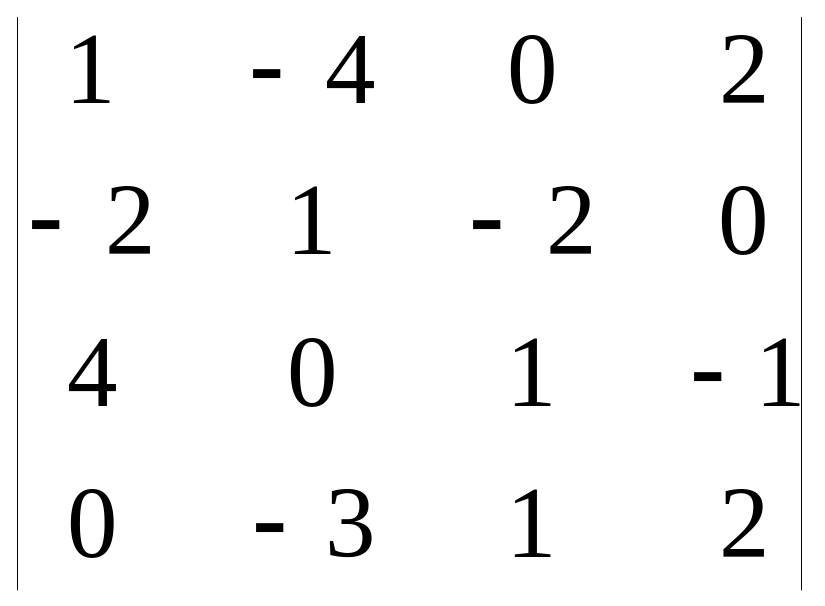

 3.3. Выучите, какими основными свойствами обладает определитель.

3.4. Вычислите определитель . Используя свойства определителей, найдите определитель:

_{а) ; б) ; в) ; г) .}

3.5. Найдите миноры и алгебраические дополнения элементов второй строки определителя .

3.6. Вычислите определитель: а) _{; б) .}

3.7. Решите уравнение и неравенство: а) б)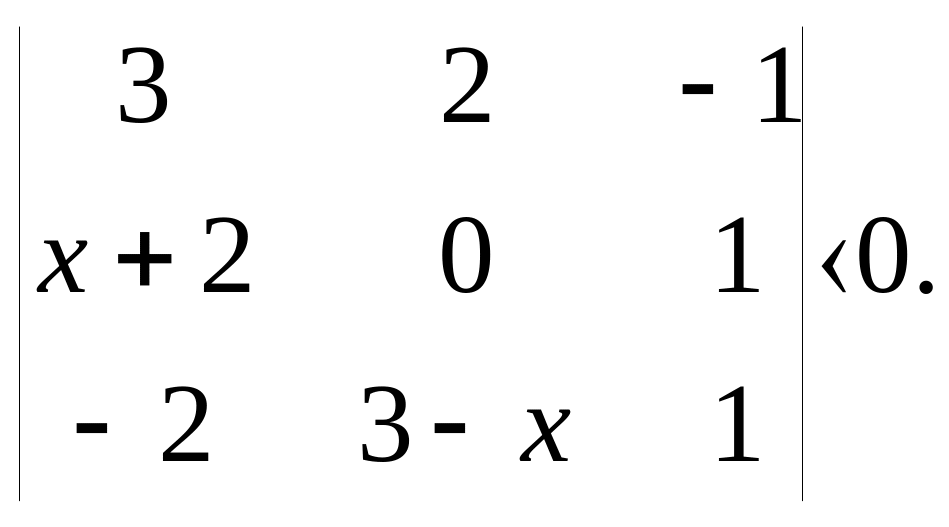

Методические указания по выполнению работы:

Каждой квадратной матрице можно поставить в соответствие неко­торое число |A|, называемое её определителем, следующим образом:

1. Второго порядка: .

2. Третьего порядка:

= .

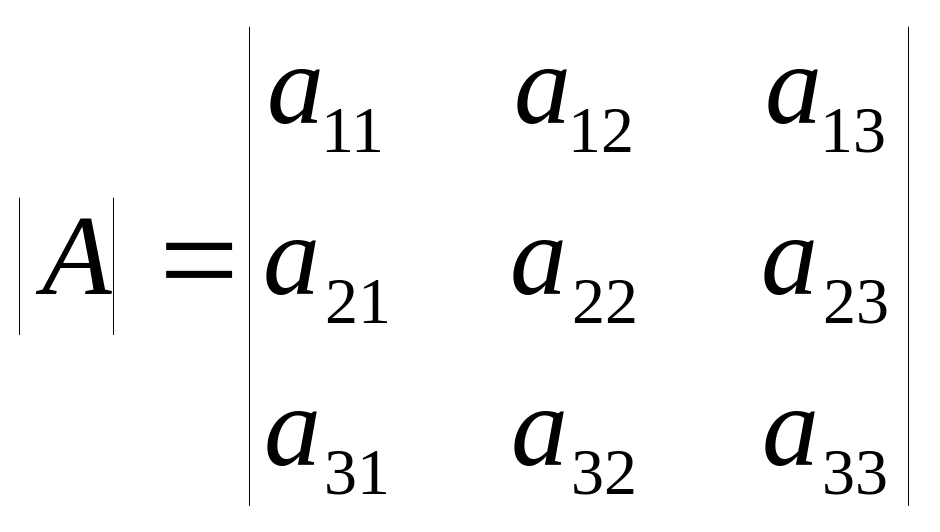3. Любого порядка. Определитель равен сумме произведений элемен­тов любой строки или столбца определителя на их алгебраические дополнения:

=

где А_ij - алгебраическое дополнение элемента а_ij : А_ij = (-1)^{i+ j} ·М_ij;

М_ij – минор элемента а_ij - новый определитель порядка (п-1), полученный из вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент а_ij.

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот (свойство равноправности строк и столбцов).

2. При перестановке двух строк или столбцов определитель меняет свой знак на противоположный.

3. Определитель с двумя одинаковыми строками или столбцами равен нулю.

4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.

Следствие: Если элементы двух строк или столбцов определителя пропор­циональны, то определитель равен нулю.

Приведем примеры нахождения определителей второго, третьего и четвертого порядков:

Пример 1. Найдите определитель |A| =

Решение: .

Ответ: |A| = 14.

Пример 2. Найдите определитель матрицы А =

Р ешение:

= 4 + 4 + 0 – 6 = 2. Ответ: |A| = 2.

Для нахождения определителя четвертого порядка необходимо уметь вычислять миноры и алгебраические дополнения элементов определителя.

Пример 3. Найдите миноры и алгебраические дополнения элементов третьего столбца определителя .

Решение:

1. Минор элемента а₁₃ (М₁₃) получаем вычеркиванием из определителя первой строки и третьего столбца:

2. Алгебраическое дополнение элемента а₁₃ (А₁₃)найдем по формуле: А₁₃=(-1)¹⁺³М₁₃;

А₁₃=(-1)⁴∙24=24.

3. М₂₃ получаем вычеркиванием из определителя второй строки и третьего столбца:

М₂₃=

4. А₂₃ найдем по формуле: А₂₃=(-1)²⁺³М₂₃;

А₂₃ = (-1)⁵∙(-11) = 11.

5. М₃₃ получаем вычеркиванием из определителя третьей строки и третьего столбца:

М₃₃= = (-1)∙(-3) - 6∙4 = 3 - 24 = -21.

6. А₃₃ найдем по формуле: А₃₃=(-1)³⁺³М₃₃;

А₃₃ = (-1)⁶∙(-21) = -21.

Ответ: М₁₃=24, А₁₃=24; М₂₃= -11, А₂₃=11; М₃₃= -21, А₃₃= -21.

Пример 4. Вычислите определитель четвертого порядка:

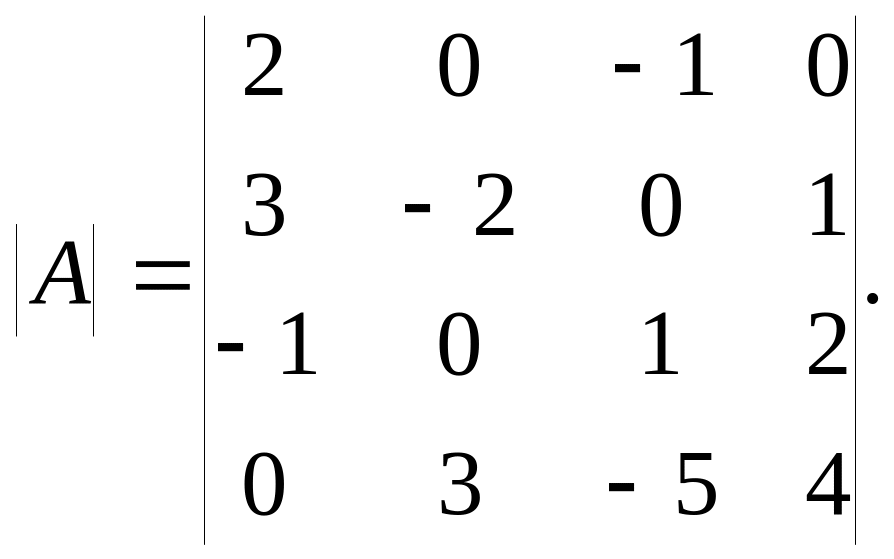
Решение:

1. Разложим определитель по элементам первой строки:

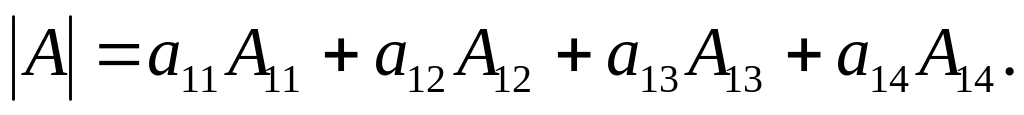
Так как а₁₁=2, а₁₂=0, а₁₃= -1, а₁₄=0, то

2. Вычислим алгебраическое дополнение А₁₁:

А₁₁=(-1)¹⁺¹М_11, где М₁₁=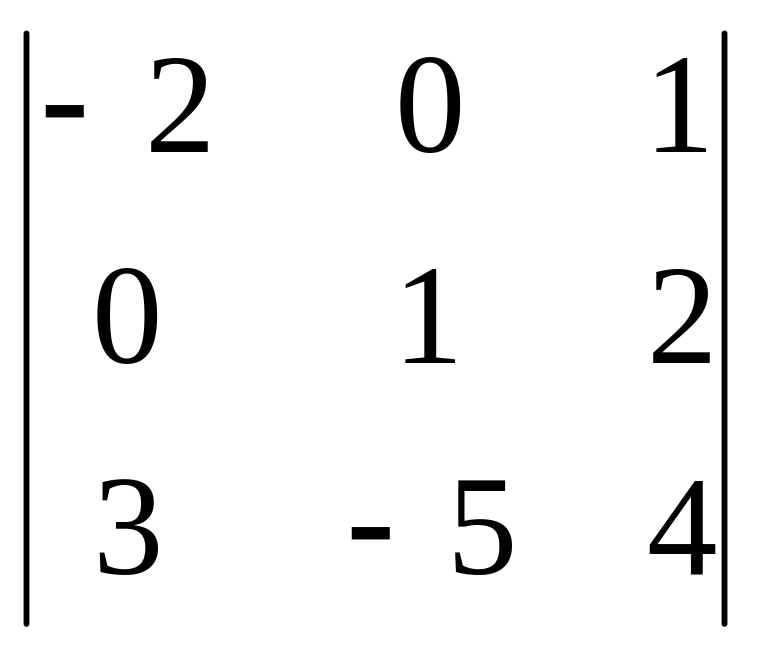 =(-2)∙1∙4+3∙0∙2+1∙0∙(-5) - (3∙1∙1+(-2)∙2∙(-5)+4∙0∙0 =

= -8+0+0-(3+20+0) = -8-23= -31.

Тогда А₁₁=(-1)²∙(-31)= -31.

3. Вычислим алгебраическое дополнение А₁₃:

А₁₃=(-1)¹⁺³М_13, где М₁₃= = 3∙0∙4+(-1)∙3∙1+0∙2∙(-2) - (1∙0∙0+4∙(-1)∙(-2)+3∙2∙3) =

=0-3+0-(0+8+18) = -3-26 = -29.

Тогда А₁₃=(-1)⁴∙ (-29) = -29.

4. Поскольку , получим:

Ответ:

Список литературы:

1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с. – Глава 2, §2.2, стр. 17 – 33.

2. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 1, § 2, стр. 71 – 78.