
- •Методические указания
- •Содержание
- •Введение
- •Цель работы
- •Теоретические основы
- •Вычислительный эксперимент
- •Численные методы решения дифференциальных уравнений в частных производных
- •Приближенное решение
- •Методы взвешенных невязок
- •Методы конечных разностей
- •Методы конечных элементов
- •Погрешность аппроксимации, согласованность, устойчивость и сходимость конечно-разностных и конечно-элементных схем
- •Ламинарное движение вязкой несжимаемой жидкости в цилиндрической трубе
- •Распределение скорости в поперечном сечении трубы
- •Расход жидкости через поперечное сечение трубы
- •Закон сопротивления Пуазейля – Хагена
- •Краткое описание структуры программы polyfem
- •Порядок выполнения работы
- •Задание к работе
- •Порядок работы с программой
- •4 Требования к отчету
- •5 Контрольные вопросы
Численные методы решения дифференциальных уравнений в частных производных
Движение жидкости описывается дифференциальными уравнениями в частных производных второго порядка с соответствующими начальными и граничными условиями. Численный метод исследования движения жидкости заключается в использовании численного метода решения этих дифференциальных уравнений.
Обозначим одно из уравнений, входящих в систему дифференциальных уравнений, в виде
![]() , (2.1)
, (2.1)
где Ф - искомая переменная;
L - краткое обозначение оператора, воздействующего на переменную Ф ,
например,
![]()
![]() .
.
Начальные и граничные условия также можно кратко записать в виде:
I(Ф) = 0, S(Ф) = 0, (2.2)
где I - оператор, например,
![]() ,
либо функция;
,
либо функция;
S - оператор, например,
![]() ,
где n - нормаль к границе
области, либо выражение.
,
где n - нормаль к границе
области, либо выражение.
Приближенное решение
Приближенное решение уравнения (2.1) представим в виде
![]() , (2.3)
, (2.3)
где
![]() - функция, выбираемая так, чтобы с
определенной точностью выполнялись
- функция, выбираемая так, чтобы с
определенной точностью выполнялись
начальные и граничные условия;
![]() - подлежащие определению коэффициенты;
- подлежащие определению коэффициенты;
![]() - система известных линейно независимых
базисных
- система известных линейно независимых
базисных
(пробных) функций, удовлетворяющих условию полноты,
то есть условию
 при
при
![]() . (2.4)
. (2.4)
Условие (2.4) гарантирует улучшение аппроксимации (2.3) при возрастании числа М используемых известных базисных функций.
Методы взвешенных невязок
Если приближенное решение (2.3) подставить в уравнения (2.1) и (2.2), то они не будут тождественно удовлетворяться. В результате появятся невязки:
![]() ,
,
![]() ,
,
![]() . (2.5)
. (2.5)
При построении приближенного решения (2.3) можно идти по одному из следующих путей:
Решение (2.3) подбирается таким образом, что дифференциальное уравнение (2.1) удовлетворяется точно, то есть R = 0, но RS 0. Такие численные методы называются граничными методами (методы граничных элементов, панельные методы).
Граничные условия (2.2) выполняются точно, то есть RS = 0, но R
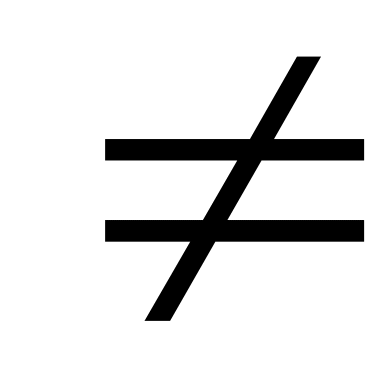 0. Такие методы называются внутренними
(методы конечных элементов,
конечно-разностные методы).
0. Такие методы называются внутренними
(методы конечных элементов,
конечно-разностные методы).
Уравнение (2.1) и граничные условия (2.2) удовлетворяются приближенно, то есть R 0, RS 0. В этом случае имеют дело со смешанными методами.
В уравнении (2.3) базисные функции
![]() полагаются известными. В качестве их
часто используются линейные или
квадратичные функции, например,
полагаются известными. В качестве их
часто используются линейные или
квадратичные функции, например,
![]() ,
,
где
![]() - некоторые постоянные, связанные с
узлом m.
- некоторые постоянные, связанные с
узлом m.
Коэффициенты
![]() или
подлежат определению. Чтобы найти эти
коэффициенты, полагается равным нулю
интеграл:
или
подлежат определению. Чтобы найти эти
коэффициенты, полагается равным нулю
интеграл:
![]() , (2.6)
, (2.6)
где
![]() - радиус-вектор точки;
- радиус-вектор точки;
![]() - область и элемент области интегрирования;
- область и элемент области интегрирования;
![]() - весовые функции.
- весовые функции.
Если в (2.6) положить m =1,2,…,M, то получится система из M уравнений для определения M неизвестных коэффициентов . Равенство (2.6) - это известное определение скалярного произведения двух функций. Если весовые функции образуют полную систему функций, то из (2.6) следует, что невязка R должна быть ортогональна каждому элементу этой системы функций. А это означает, что невязка R в среднем стремится к нулю (в пределе, когда ). В случае конечных значений M, чем больше M, тем меньше в среднем невязка R отличается от нуля.
Уравнение (2.6) отражает суть метода взвешенных невязок (МВН). Выбирая различные весовые функции , можно построить различные численные методы. Большинство современных численных методов решения уравнений (2.1), (2.2) являются частными случаями МВН. К этим частным случаям относятся широко применяемые в МЖГ методы конечных разностей (МКР) и методы конечных элементов (МКЭ). В литературе МВН иногда называют проекционно-разностными методами.
