Цель работы
Целью работы являются:
ознакомление с численными методами исследования движения жидкости;
изучение методов получения точных решений уравнений Навье-Стокса ламинарного движения вязкой несжимаемой жидкости в цилиндрических трубах эллиптического и круглого сечений;
получение практических навыков численного исследования на примере изучения ламинарного движения вязкой несжимаемой жидкости в цилиндрической трубе.
Теоретические основы
Вычислительный эксперимент
В МЖГ для решения задач используются три различных подхода: экспериментальный (физический эксперимент), теоретический (аналитический) и численный (вычислительный). В таблице 2.1 приведено сравнение различных подходов /1/.
Таблица 2.1
Подход |
Преимущества |
Недостатки |
Экспериментальный |
Получение наиболее близких к реальности результатов |
1. Сложное оборудование 2. Проблемы моделирования 3. Коррекция измеренных значений 4. Сложность измерений 5. Стоимость |
Теоретический |
Получение "чистой" информации общего характера, обычно в виде формул |
1. Ограничен простыми геометрическими конфигурациями и физическими моделями 2. Обычно применим лишь к линейным задачам |
Численный |
1. Нет ограничений, связанных с линейностью 2. Описание сложных физических процессов 3. Описание эволюции течения во времени |
1. Погрешности округления 2. Проблема задания граничных условий 3. Стоимость ЭВМ |
С появлением быстродействующих компьютеров роль и значение численного исследования гидродинамических задач существенно возросли.
Отправным пунктом любого численного исследования является некоторая физическая модель. Под физической моделью понимают схему или описание какого-либо физического предмета, процесса или явления, основанных на упрощениях и постулатах. Упрощения, как правило, касаются второстепенных факторов, несущественных свойств и механизмов явлений. В МЖГ имеют дело в основном с двумя типами физических моделей: моделями вещества (идеальная несжимаемая жидкость, вязкая жидкость, совершенный газ и т. д.) и моделями постановок задач в рамках выбранных моделей вещества для рассматриваемых объектов (поток газа, обтекающий крыло, занимает все пространство, одномерное движение жидкости в трубе и т. д.).
Между вычислительным экспериментом и физической моделью существует ряд этапов, вносящих свои ограничения. На рисунке 2.1 эти этапы показаны в виде блок-схемы. Математическая модель - это приближенное математическое описание физической модели. При ее создании обычно вводятся упрощающие предположения, которые необходимо знать, чтобы правильно использовать математическую модель.
Физическая модель |
Математическая модель
|
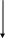
Дискретная аппроксимация
|
-
Численный алгоритм
-
Программа моделирования
-
Вычислительный эксперимент
Рисунок 2.1
В МЖГ при численном решении задач математическими моделями являются, как правило, дифференциальные уравнения в частных производных. Сложность и тип дифференциальных уравнений зависят от решаемых задач. Например, при расчете поля давления вокруг удобообтекаемого тела можно использовать уравнения Эйлера, а при расчете силы сопротивления, оказываемой неудобообтекаемым телом, - уравнения Навье-Стокса или уравнения Рейнольдса.
Дискретная аппроксимация заключается
в следующем. Непрерывная расчетная
область
заменяется дискретной расчетной
областью
,
состоящей из отдельных точек, называемых
узлами. Совокупность узлов составляет
сетку
,
которая может быть равномерной или
неравномерной, с четырехугольными
ячейками или треугольными. Расстояния
между узлами сетки называют шагами.
Процедура приближенной замены
дифференциальных уравнений, граничных
и начальных условий их дискретными
аналогами зависит от численного алгоритма
или от выбранного численного метода.
На этапе разработки численного алгоритма (смотрите рисунок 2.1) ищется наилучший компромисс между качеством его представления и вычислительными затратами. Можно выбрать разностную схему с очень высоким порядком погрешности аппроксимации и с очень мелкими шагами сетки. Но если возникающие десятки или сотни тысяч алгебраических уравнений не могут быть быстро решены на компьютере, то выбранный численный алгоритм становится невозможным. Очевидно, что численный алгоритм влияет на выбор способа дискретизации.
После разработки численного алгоритма можно строить программу моделирования. Качественно разработанная программа должна быть удобочитаемой и несложной в использовании. В случае необходимости - легко модифицируемой. Она должна иметь четкую модульную структуру и встроенную диагностику. Заранее спроектированная структура должна собираться только из проверенных программных компонентов или модулей. Полная программа должна быть испытана на известных задачах для проверки алгоритма (тестовых задачах). Только когда испытания и тестирование завершены, программу можно считать готовой для проведения вычислительного эксперимента.