1.3.2 Варіанти завдань
Додати, знайти різницю, перемножити та розділити двійкові числа:
Варіант |
Числа |
Варіант |
Числа |
1 |
1011010001.101101 11011.011 |
9 |
1111010001.111101 10011.001 |
2 |
1111010001.1010101 10011.001 |
10 |
1011110001.101001 11011.011 |
3 |
1011010101.001101 11011.011 |
11 |
1011011001.100101 11111.111 |
4 |
1011010011.111101 11101.110 |
12 |
1011010001.101101 10001.101 |
5 |
1011010001.101101 10011.001 |
13 |
1011011101.111101 11001.011 |
6 |
1010110001.100111 10010.101 |
14 |
1011011001.101001 10111.111 |
7 |
1111011001.101111 11001.111 |
15 |
1011010101.100001 11001.001 |
8 |
1011110001.100101 11001.001 |
16 |
1011010011.001101 10011.001 |
Лабораторна робота №4
Тема роботи: Логічні операції з двійковими числам
Мета роботи: Навчитися виконувати логічні операції здвійковими числами.
1.4.1 Основні теоретичні відомості
Існують три унарні логічні операції. Дві з ниє є тривіальними:
x |
y1=f1(x) |
y2=f2(x) |
0 |
1 |
0 |
1 |
1 |
0 |
y1 – константа одиниці (абсолютно істинна функція); y2 – константа нуля (абсолютно істинна функція). Єдина нетривіальна функція – це логічне заперечення (НЕ) (інверсія, не x, NOT):
x |
y3=f3((x) |
0 |
1 |
1 |
0 |
Крім описаних ще є операція повторення:
x |
y4=f4(x) |
0 |
0 |
1 |
1 |
Функцій двох змінних. є 16. Їхні назви та таблиці значень:
-
Позначення функції
Найменування функції
a
Примітка
0
0
1
1
b
0
1
0
1
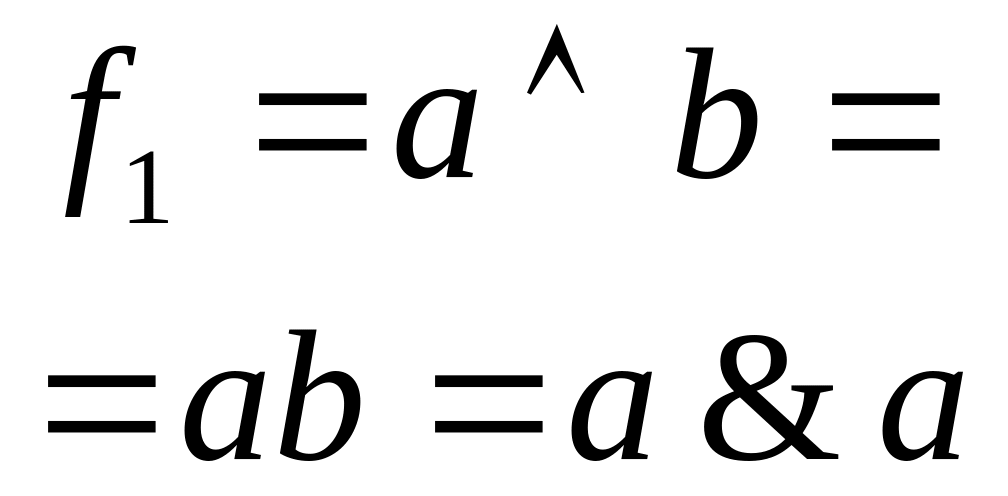
Кон'юнкція (логічне множення)
0
0
0
1
AND
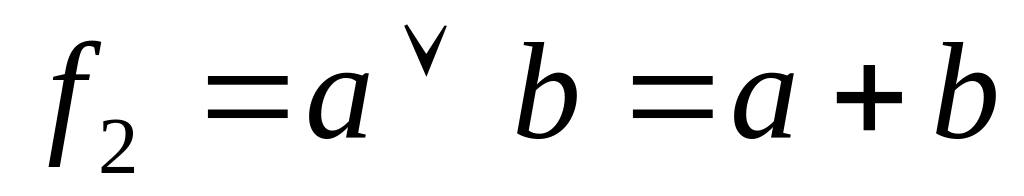
Диз'юнкція (логічне додавання)
0
1
1
1
OR
Імплікація (від a до b)
1
1
0
1
Обернена імплікація (від b до a)
1
0
1
1
Рівносильність
1
0
0
1
Нерівносильність (сума за модулем)
0
1
1
0
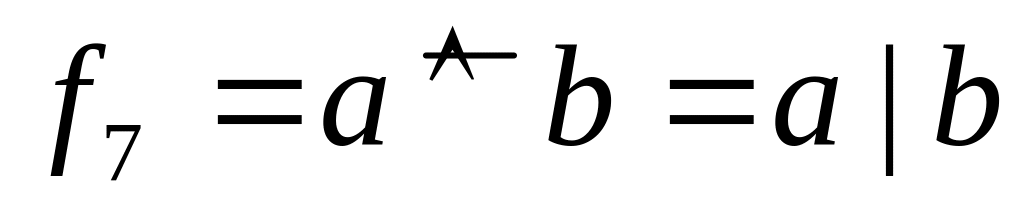
Функція Шеффера (інферсія кон'юнкції)
1
1
1
0
Функція Пірса-Вебба (інверсія диз'юнкції)
1
0
0
0
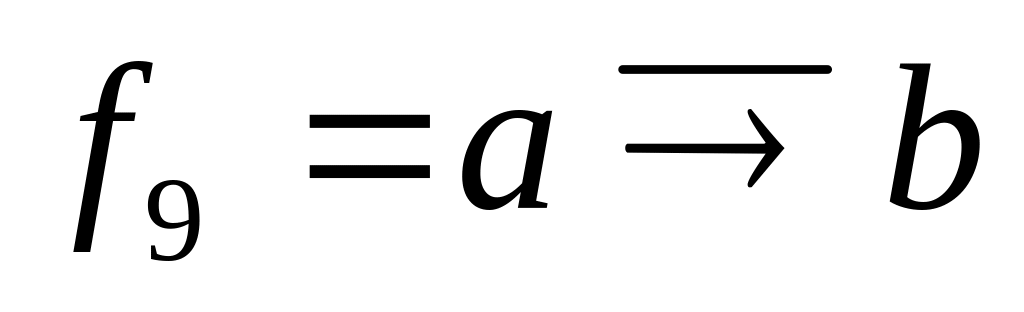
Інферсія імплікації (функція заборони за b)
0
0
1
0
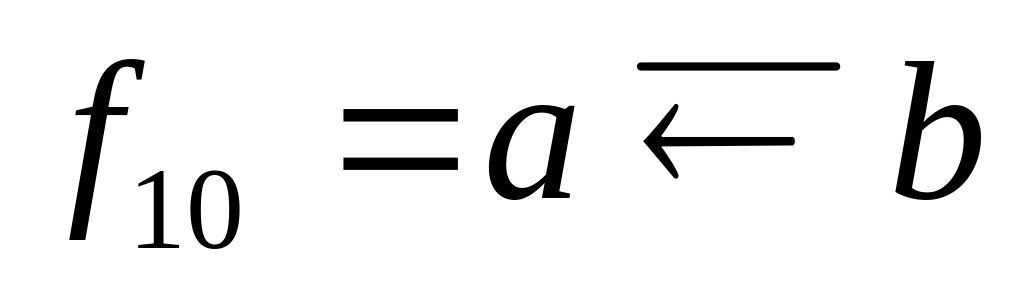
Інферсія імплікації (функція заборони за a)
0
1
0
0
Повторення a
0
0
1
1
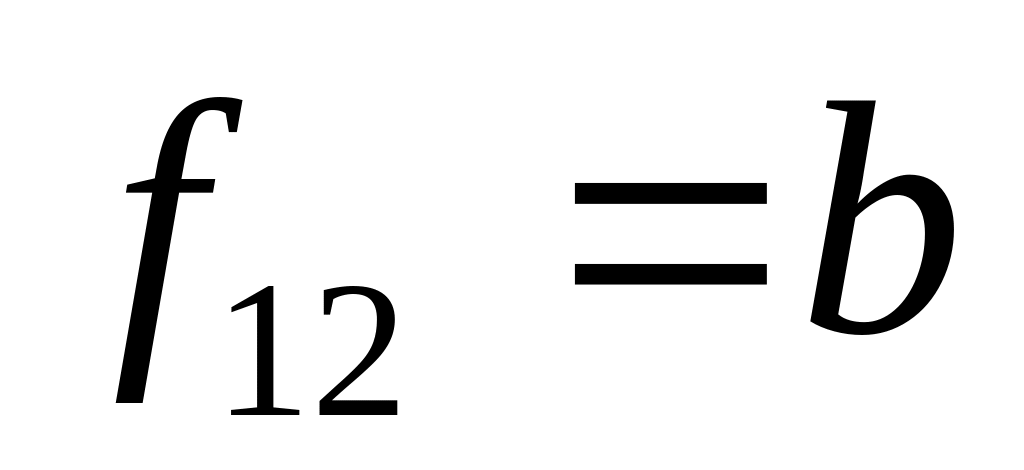
Повторення b
0
1
0
1
Інверсія a (функція НЕ a)
1
1
0
0
Інверсія b (функція НЕ b)
1
0
1
0
Одинична функція (конастанта 1)
1
1
1
1
Нульова функція (конастанта 0)
0
0
0
0
Приклад операції NOT: NOT(100110111)=011001000.
Приклад операції AND: 11011001 AND 00110001 = 00010001.
Приклад операції OR: 10011100 OR 10100111 = 10111111.