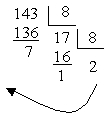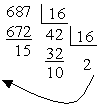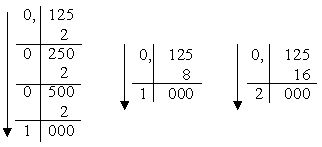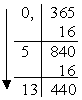1.1.1. Основні теоретичні відомості

Двійкові числа записуються за допомогою двох цифр 0 і 1. Їх позиція в числі відповідає певному степіню 2. Приклади:

(5)₁₀ = (101)₂ = 1·2² + 0·2¹ + 1·2⁰ (15)₁₀ = (1111)₂ = 1·2³ + 1·2² + 1·2¹ + 1·2⁰.

Окрім двійкової системи числення в обчислювальній техніці і програмуванні значне місце займають вісімкова й шістнадцяткова системи числення. Вони використовуються для скороченого запису двійкових кодів.

У вісімковій системі числення в якості цифр використовують символи: 0, 1, 2, 3, 4, 5, 6, 7. В шістнадцятковій системі потрібно 16 символів, в якості яких використовують арабські цифри і п'ять букв латинського алфавіту, що утворюють послідовність (із врахуванням ваги шістнадцяткових цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, E, F. Приклади:

(75,67)₈ = 7·8¹ + 5·8⁰ + 6·8^-1 + 7·8^-2 (1FC,B)₁₆ = 1·16² + 15·16¹ + 12·16⁰ + 11·16^-1

Десяткові еквіваленти символів A, B, C, D, E, F: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15

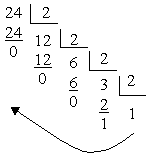
Переведення цілого числа з десяткової системи числення у 2-у, 8-у або 16-у здійснюється шляхом послідовного ділення числа на основу нової системи числення. Ділення виконується до тих пір, поки остання частка не стане менше дільника. Отримані остачі від ділення, взяті у зворотному порядку, будуть значеннями розрядів числа в новій системі числення. Остання частка дає старшу цифру числа.

Приклад: (24)10 = (?)2		(24)10 = (11000)2
Приклад: (143)10 = (?)8		(143)10 = (217)8
Приклад: (687)10 = (?)16		(687)10 = (2AF)16

Для переведення правильного дробу з десяткової системи числення у будь-яку іншу потрібно помножити заданий дріб на основу нової системи числення. Отримана ціла частина добутку буде першою цифрою після коми дробу в новій системі числення. Далі по черзі множаться дробові частини добутків на основу нової системи. Отримані цілі частини добутків будуть цифрами дробу у новій системі числення. Цей процес продовжують до тих пір, поки не буде знайдено число із заданою точністю.

Приклад: ( 0,125 )10 = ( ? )2; ( 0,125 )10 = ( ?)8; ( 0,125 )10 = (?)16.		( 0,125 )10 = (0,001)2; ( 0,125 )10 = (0,1)8; ( 0,125 )10 = (0,2)16.
Приклад: (0,365)10 = (?)16		(0,365)10 = (0,5D)16

Для переведення змішаного числа з десяткової системи числення в іншу необхідну окремо перевести цілу й дробову частини за вказаними правилами, а потім об'єднати результати у змішане число.

Якщо основа нової системи числення дорівнює деякому степеню старої системи числення, то алгоритм переводу дуже простий: потрібно згрупувати справа наліво розряди в кількості, що дорівнює показнику степеня і замінити цю групу розрядів відповідним символом нової системи числення. Цим алгоритмом зручно користуватися коли потрібно перевести число з двійкової системи числення у вісімкову або шістнадцяткову. Наприклад, 10110₂=10 110=26₈, 1011100₂=101 1100=5C₁₆.

Перевід у двійкову истему виконується за допомогою зворотнього правила: один символ старої системи числення замінюється групою розрядів нової системи числення, в кількості, рівній показнику степеня нової системи числення. Наприклад, 472₈=100 111 010=100111010₂, B5₁₆=1011 0101=10110101₂.