1.3. Зонная диаграмма р-n-перехода при наложении внешнего поля

Р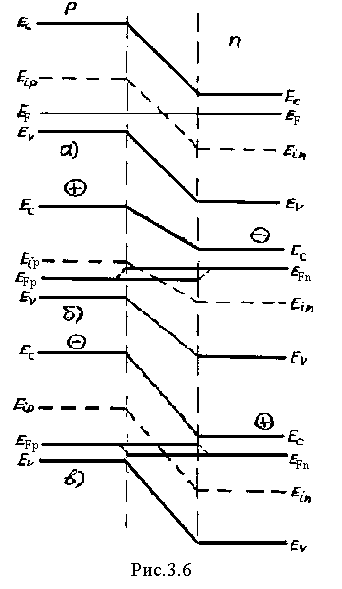 ассмотрим изменение зонной диаграммы при наложении на переход внешнего напряжения. При этом следует иметь в виду, что «плюс» внешнего источника опускает уровни энергии в зонной диаграмме, а «минус» поднимает. При наложении внешнего поля нарушается термодинамическое равновесие, и уровни Ферми заменяются на квазиуровни Ферми, т.е. уровнями Ферми при определенном поле. Полем в толще полупроводника пренебрегаем, т.е. считаем, что зоны идут без наклона (горизонтально). Это означает, что практически все внешнее напряжение падает на р-n-переходе, а падение напряжения на электронейтральных частях полупроводника близко к нулю.

Н а рис.3.6 приведены зонные диаграммы р-n-перехода в равновесном состоянии (а), при прямом (б) и при обратном (в) включении. При наложении внешнего поля в прямом направлении изгиб зон в р-n-переходе уменьшается и становится равен:

q(V_K-U), (3.13)

где U- внешнее смещение в прямом направлении.

Квазиуровни Ферми для основных носителей заряда в n-области (Е_Fn) и основных носителей в р-области E_Fp сдвигаются друг относительно друга на qU, т.е.

Е_Fn-Е_Fр=qU. (3.14)

Для тонкого р-n-перехода допустимо считать квазиуровень Е_Fр неизменным во всей р области, а также во всем переходе. Пунктиром условно нанесены квазиуровни Ферми для неосновных носителей заряда в каждой из областей. Вдали от р-n-перехода они совпадают с квазиуровнями для основных носителей заряда, т.е. с уровнем Ферми для каждой из областей.

При наложении внешнего поля в обратном направлении (см. рис. 3.6 в) изгиб зон на р-n-переходе увеличивается и оказывается равным

q(V_K+U_ОБР),

где U_ОБР – обратное напряжение.

1.4. Вах тонкого р-n-перехода

Тонким р-n-переходом называют электронно-дырочный переход, толщина которого столь мала, что можно пренебречь процессами рекомбинации и генерации в области объемного заряда р-n-перехода. То есть, если известна плотность потока дырок j_p или электронов j_n в каком либо сечении р-n-перехода, то она будет такой же в любом другом сечении р-n-перехода.

Из формул (3.6) и (3.7) можно записать концентрацию электронов n_pгр на границе запирающего слоя в р-области и концентрацию дырок р_nгр на границе запирающего слоя в n-области:

(3.15)

(3.16)

При этом E_ip и Е_in принимают значения, соответствующие границам.

Для неосновных носителей заряда вдали от р-n-перехода можно записать:

(3.17)

(3.18)

В формулах (3.17) и (3.18) произошла замена квазиуровней по сравнению с формулами (3.15) и (3.16), т.к. в электронейтральной части полупроводника вдали от р-n-перехода в р области Е_Fр=Е_Fn, а в области n Е_Fn=Е_Fр.

Разделим левые и правые части выражений (3.15) и (3.17) друг на друга:

откуда

(3.19)

Разделим левые и правые части выражений (3.16) и (3.18) друг на друга:

откуда

(3.20)

При Е_Fn-Е_Fр>0, т.е. при прямом включении р-n-перехода n_ргр>n_p0 p_nгр>p_n0.

Избыточная концентрация неосновных носителей заряда на границах в этом случае равна:

(n_p)₀=n_pгр-n_p0=n_p0( ), (3.21)

(p_n)₀=p_nгр-p_n0=p_n0( ). (3.22)

Эта избыточная концентрация появляется вследствие инжекции носителей заряда через р-n-переход. n и р являются функциями расстояния от p-n-перехода n_p=f(x_p) и p_n=f(x_n).

Н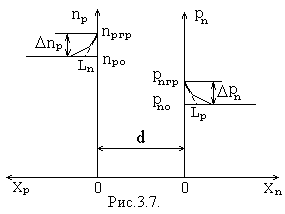 а рис. 3.7 показано изменение избыточной концентрации неосновных носителей от расстояния от области р-n-перехода.

Электроны, инжектированные в р-область, притягивают к себе дырки из объема этой области, так что вне р-n-перехода сохраняется электронейтральность. Недостаток же носителей заряда в объеме пополняется через контакт. Аналогично дырки, инжектированные в n-область притягивают к себе электроны из объема этой области, где также сохраняется электронейтральность. Глубина проникновения инжектированных носителей определяется их рекомбинацией. Неосновные носители рекомбинируют с основными, поэтому концентрация неосновных носителей падает с расстоянием и равна:

(3.23)

(3.24)

где L_n, L_p- расстояние от границы р-n-перехода, на котором концентрации неосновных носителей уменьшается в е раз, которое называется диффузионной длиной,где e – основание натурального логарифма.

Заметим, что при приложении прямого смещения запирающий слой сужается. При обратном смещении р-n-перехода он расширяется и:

Е_Fn-Е_Fр=qU<0.

Тогда для обратного включения n_pгр<n_n0. В этом случае наблюдается проникновение неосновных носителей заряда через р-n-переход из областей, прилегающих к р-n-переходу. Выражения (3.213.24) сохраняются и в этом случае. Однако избыточная концентрация здесь имеет отрицательный знак (n_p)₀<0; (p_n)₀<0. Т.е. в этом случае мы имеем дело не с избыточной, а с недостаточной концентрацией неосновных носителей.

Переход можно считать тонким, если d<L_n и d<L_p т.е. если толщина перехода меньше диффузионных длин носителей заряда.

Плотность диффузионного тока через границы при любой полярности внешнего напряжения равна:

(3.25)

(3.26)

Подставим в (3.25) и (3.26) выражения (3.23) и (3.24) и получим с учетом (3.21) и (3.22):

(3.27)

(3.28)

Так как мы предполагали, что плотности электронов и дырок одинаковы в любом сечении р-n-перехода и на его границах, а также, поскольку движение электронов и дырок противоположно друг другу, то ВАХ р-n-перехода можно представить в виде:

(3.29)

Уравнение (3.29) фактически определяет плотность тока, текущего через запорный слой, в зависимости от внешнего напряжения. Если площадь р-n- перехода S, то полный ток через переход равен I=jS. Тогда вольтамперную характеристику р-n-перехода можно записать в виде:

(3.30)

где - ток насыщения р-n-перехода или обратный тепловой ток.

Вольт-амперная характеристика идеального р-n-перехода представлена на рис. 3.8. Величина обратного тока с увеличением обратного напряжения стремится к величине I_S.

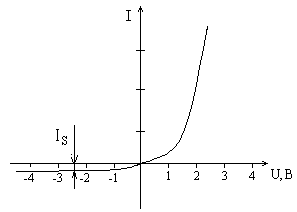
Рис. 3.8.