Планирование работ на основе трехфазной модели вс
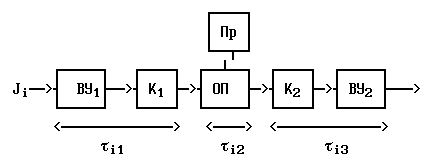
фаза ввода- устройство ввода ВУ1 и канал К1;
фаза обработки- процессор Пр- оперативная память;
фаза вывода- канал К2 и устройство ВУ2.
Рис.11.5.
Допускается одновременное выполнение не более трех работ:одна
в фазе ввода, другая в фазе обработки,третья в фазе вывода.
Исходной для планирования работ является матрица трудоемкости Т.
С. Джонсон доказал ,что при выполнении хотя бы одного из следующих
ограничений
;
(26.1)
(26.2)
Алгоритм оптимального планирования работ в трехфазной модели
сводится к алгоритму на основе двухфазной модели.
В этом случае трехстолбцовая матрица трудоемкости преобразу-
ется в двухстолбцовую матрицу путем путем попарного сложения эле-
ментов I и II столбцов, а также элементов II и III столбцов.
Элементы vi1 и vi2 новой матрицы определяются следующим образом:
,для i=[1..M]
К полученной матрице применяется ранее рассмотренный алгоритм.
ПРИМЕР . Упорядочить работы по критерию минимума T для трехфазной модели ВС.
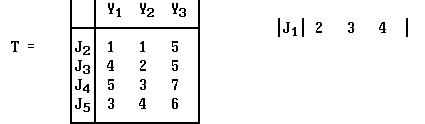
Эта матрица имеет характеристики
min(
)
= 1 ;
max(
)
= 4 ;
min(
)
= 4 ;
=> выполняется ограничение (26.2) и задача планирования сводится к планированию на основе двухфазной модели.
Двухстолбцовая матрица:
Диаграмма выполнения этих работ:
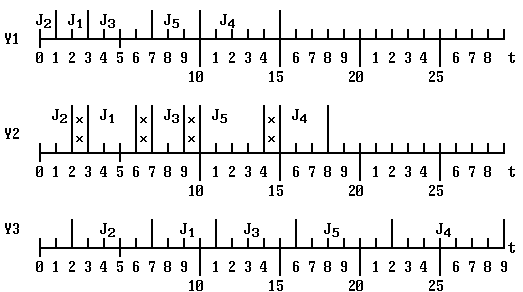
Рис.11.6.
Степень совмещения работы устройств
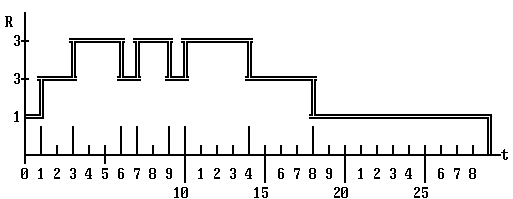
Рис.11.7.
Суммарное время выполнения работ составляет 29 единиц.
Устройство Y1 ввода работает- 15 единиц,
Устройство Y2 ввода работает- 13 единиц,
Устройство Y3 ввода работает- 27 единиц.
Коэффициент загрузки устройств:
q1 = 0.56; q2 = 0.45; q3 = 0.93.
Ненормированная суммарная загрузка устройств системы составляет
R* = q1 + q2 + q3 = 1.9
Средняя (нормированная) загрузка устройств R = R* / 3 = 0.63;
Если ограничения (1) и (2) не выполняются, не существует метода точного решения задачи планирования кроме метода простого перебора. Но на практике приходится решать задачи планирования работ более, чем с тремя устройствами. В этих случаях используют эвристические алгоритмы, позволяющие получить не оптимальный, но достаточно хороший план.
11.1.3. Эвристический алгоритм планирования работ в вс
Алгоритм (для 3-х фазных систем):
1. Выделяется номер фазы "k" с наибольшей суммарной продолжительностью работ, т.е.
max(
);
2. Если k = 1, то работы запускаются в порядке убывания величин
;
3. Если k=3, то работы запускаются в порядке возрастания величин
4. Если k=2, то работы упорядочиваются на основе алгоритмов 2-х фазного планирования, причем из матрицы трудоемкости исключается второй столбец.
Эффективность эвристических методов планирования характеризуется степенью близости суммарного времени выполнения работ T к минимально возможному времени T 0;
Определим T0
Анализируем матрицу трудоемкости T, выделяем фазу "k", суммарная продолжительность работ в которой имеет максимальное значение, т.е. определим
фазу k = 1, ... ,N из условия:
=> в отрезок T2 можно уложить большинство работ, выполняемых на менее трудоемких фазах l = 1, ...,k-1,k+1, ..., N, за исключением работы, которая должна быть выполнена сначала в фазах 1,2, ...,k-1 до начала обработки в фазе k и работы, которая должна быть завершена после окончания отрезка времени T2 на фазах k+1, ...,N.
Необходимо выбрать в качестве этих 2-х работ такие, чтобы продолжительность их до k-й фазы и после k-й фазы была минимальной.
Продолжительность выполнения первой запускаемой работы определяется значением
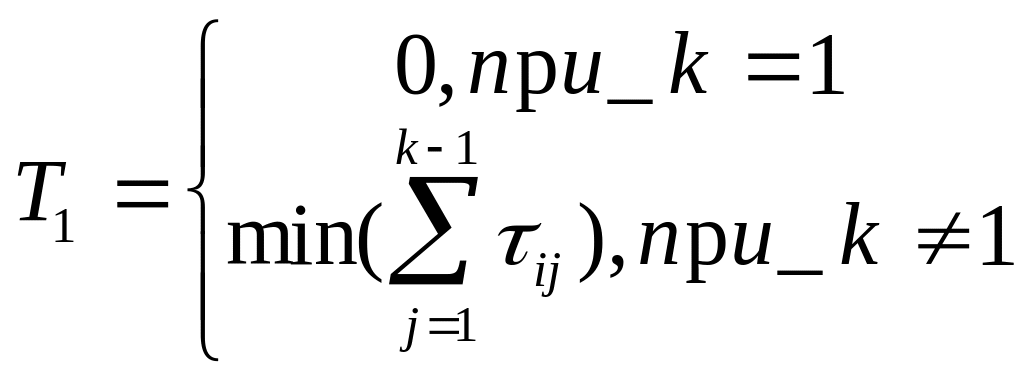
Продолжительность завершения работ на фазах k+1, ...,N определяется значением:
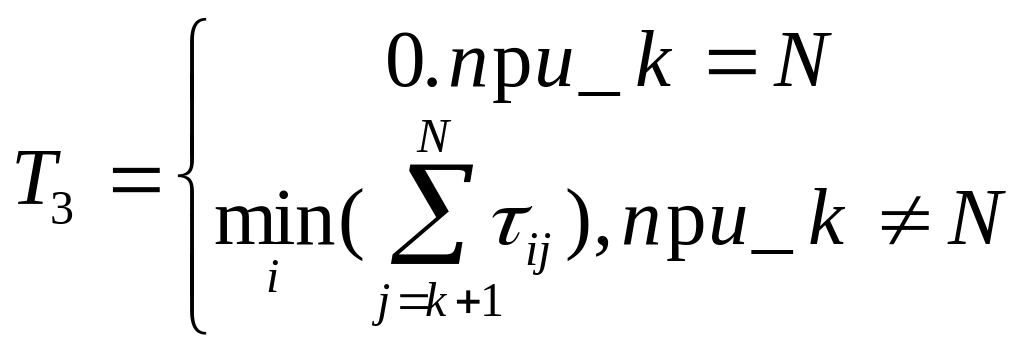
Минимально возможное время выполнения совокупности работ
T0
= T1
+ T2
+ T3
=
+
+
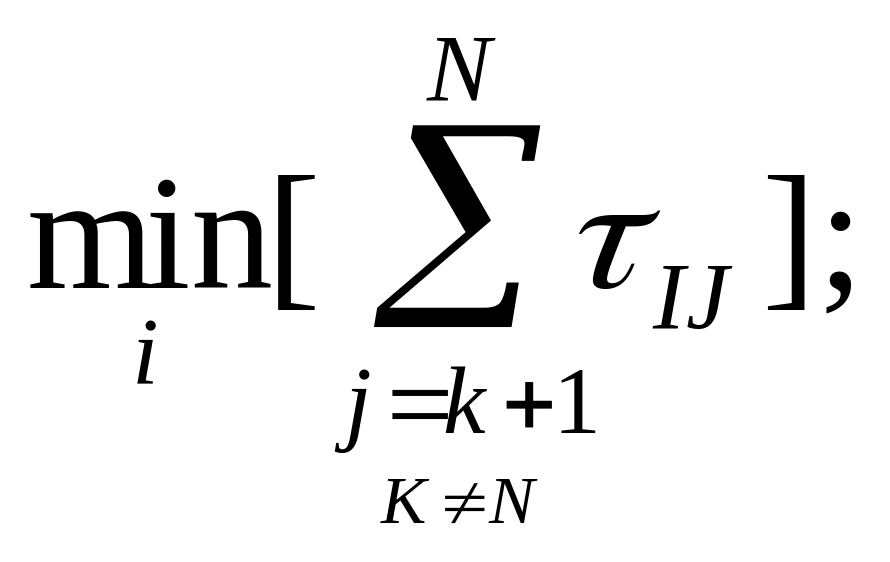
где n- номер фазы с максимальной суммарной продолжительностью работ.
Пример . Упорядочить работы с использованием эвристического алгоритма.
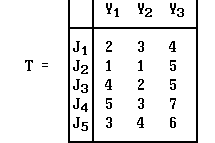
1. Суммарные трудоемкости фаз 1,2,3 равны соответственно
(2+1+4+5+3) = 17
(3+1+2+3+4) = 13
(4+5+5+7+6) = 27
=> Максимально трудоемкой является фаза k = 3;
При k = 3 работы следует запустить в порядке возрастания величин
Эти величины имеют значения:
J1 J2 J3 J4 J5
5 2 6 8 7
=> работы должны запускаться в следующем порядке:
J2 ,J1 ,J3 ,J5 ,J4 .
Оценим минимально возможное время выполнения этих работ
T0 = 2 + 27 +0 =29, что совпадает с ранее приведенным примером.