1. Планирование работ на основе двухфазной модели вс

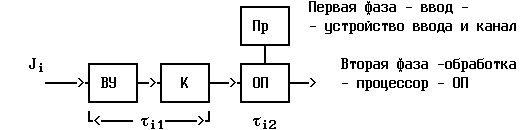
Рис.11.3.

Продолжительность выполнения работ J₁, ..., J_M в первой фазе равна,

во второй фазе - .

Алгоритм оптимального планирования работ С.Джонсона по

критерию минимума суммарного времени выполнения работ:

1. Отметим начало очереди работ позицией а=1, конец очереди позицией b = M.

2. В матрице трудоемкости T находится минимальное значение

3. Выделяются работы J₁, ... , Jw для которых

4. Если выделена единственная работа J_{L ,} то при она ставится в начало очереди, определяемое позицией "a", а при в конец очереди в позицию "b".

Затем выполняется п.7.

5. Если выделено несколько работ J₁, ..., Jw , то они разделяются на две группы:

1) с одинаковыми значениями ,равными .

2) с одинаковыми значениями , равными .

6. Работы из первой группы заносятся в начало очереди в позиции "a", "a+1", ..."b" в порядке увеличения значения Работы из второй группы заносятся в конец очереди в позиции "b", "b-1", ... в порядке увеличения значений .

7. После включения работы в очередь (в позицию "a" или "b") работа вычеркивается из матрицы трудоемкости и переменной "a" или "b" присваивается новое значение "a":="a"+1 или "b":="b"-1.

8. Процесс продолжается от пункта 2. до распределения всех работ по позициям очереди.

Пример

Дано: матрица трудоемкости T:

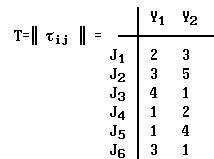
Упорядочим работы по критерию минимума T

1) Присваиваем a = 1, b = 6.

2) Находим минимальное значение = 1.

3) Выбираем работы, для которых .

Y₁ Y₂

J₃ 4 1

J₄ 1 2

J₅ 1 4

J₆ 3 1

4) Разделяем работы на группы с одинаковыми значениями

и

Y₁ Y₂ Y₁ Y₂

J₄ 1 2 J₃ 4 1

J₅ 1 4 J₆ 3 1

5) В соответствии с алгоритмом работы J₄ и J₅ включаются в начало очереди в позиции "a" и "a+1", т.е. в позиции 1 и 2.

Работы J ₃ и J₆ включаются в конец очереди в позиции 5 и 6.

Следовательно , план работ имеет вид:

1 2 3 4 5 6

J₄ J₅ ? ? J₃ J₆

6) Начало и конец очереди отмечаем позициями "a"="a+2"

"b"="b-2". Итак , "a"=3 , "b"=4.

После вычеркивания распределенных работ J₄, J₅, J₃, J₆.

Матрица трудоемкости :

Y₁ Y₂

T= J₁ 2 3

J₂ 3 5

7. Минимальное . В соответствии с алгоритмом работу J₁ включаем в начало очереди в позицию "a" = 3, а работу J₂ в позицию "b" = 4.

Окончательно план имеет вид:

1 2 3 4 5 6

J₄ J₅ J₁ J₂ J₃ J₆

Диаграмма выполнения этих работ:

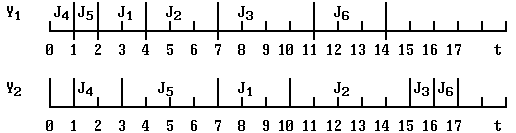
Рис.11.4.

Из диаграммы видно, что время выполнения 6 работ T = 17. При

любой другой последовательности запуска работ это время будет

только больше.