1.3 Вычислить

Решение:

3.20 Вычислить

Решение

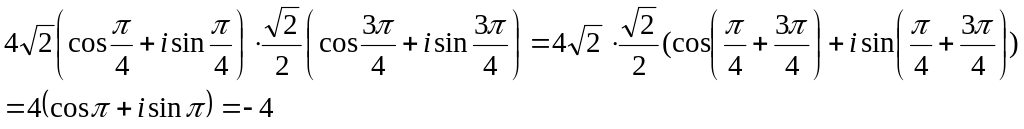
3.21 Найти .

Решение Запишем сначала число в тригонометрической форме:

; , .

По формуле Муавра имеем

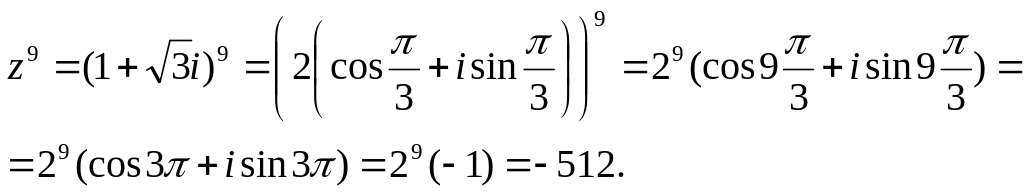
3.22 Найти частное .

Решение: .

3.23 Вычислить

Решение

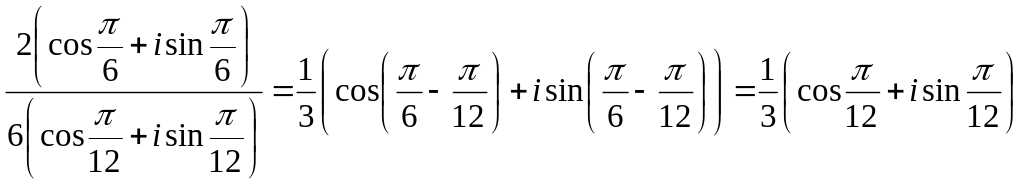
3.24 Найти .

Решение. Запишем подкоренное выражение в тригонометрической форме . По формуле

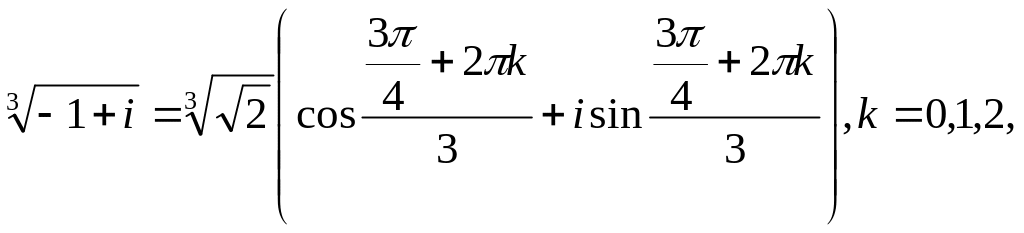
Откуда получаем три значения корня

при ,

при ,

при .

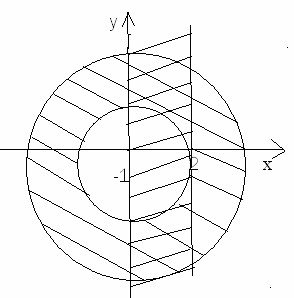
3.25 Изобразите на рисунке множество точек комплексной плоскости, удовлетворяющих условию:

Решение: 1) Запишем z в алгебраической форме , тогда . Найдем . Тогда

(возведем в квадрат),

.

- окружность с центром и радиусом 2. Неравенство задает множество точек, лежащих за пределами окружности.

- окружность с центром и радиусом 4. Неравенство задает множество точек, лежащих внутри окружности.

2) , т.е. получаем неравенства .

Решением является пересечение заштрихованных областей.

3.26 Найдите все корни уравнения .

Решение. .

.

.

3.27 Найти sin(1+2i).

Решение:

3.28* Найти вычет функции относительно точки z = 2.

Решение: Эта точка является полюсом второго порядка. Получаем:

3.29* Вычислить определенный интеграл .

Решение: Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.

Найдем вычет функции

Получаем

3.30* Вычислить определенный интеграл

Решение: Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.

Найдем вычет функции

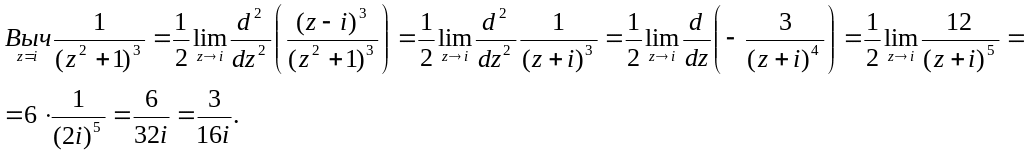Получаем

3.31 Восстановить аналитическую функцию по ее действительной и или мнимой части:

Восстановить аналитическую функцию по ее мнимой части можно двумя способами.

Решение.

Первый способ.

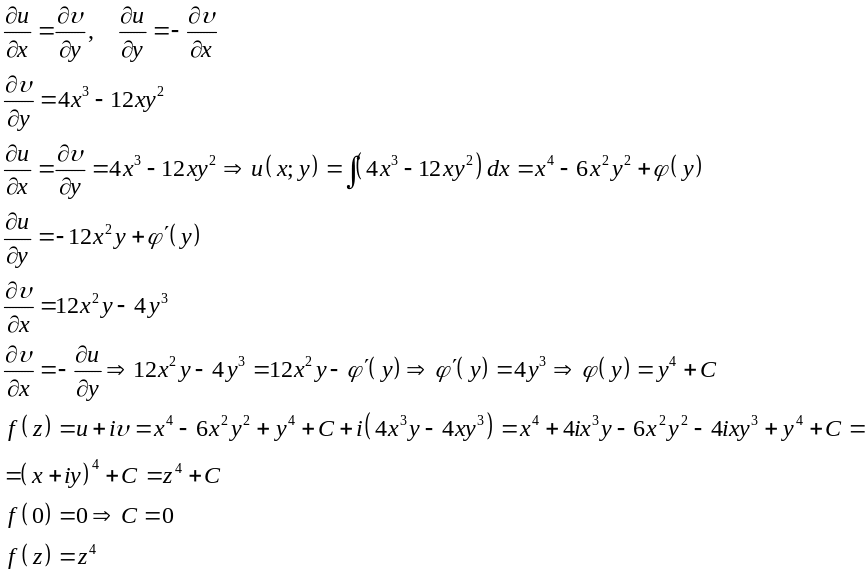
Второй способ.

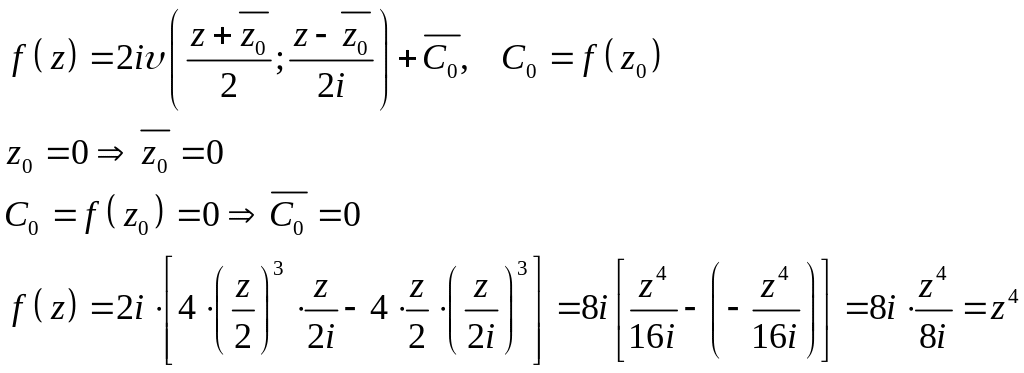
3.32* .Вычислить:

а) , L – дуга окружности от точки , до точки

б)

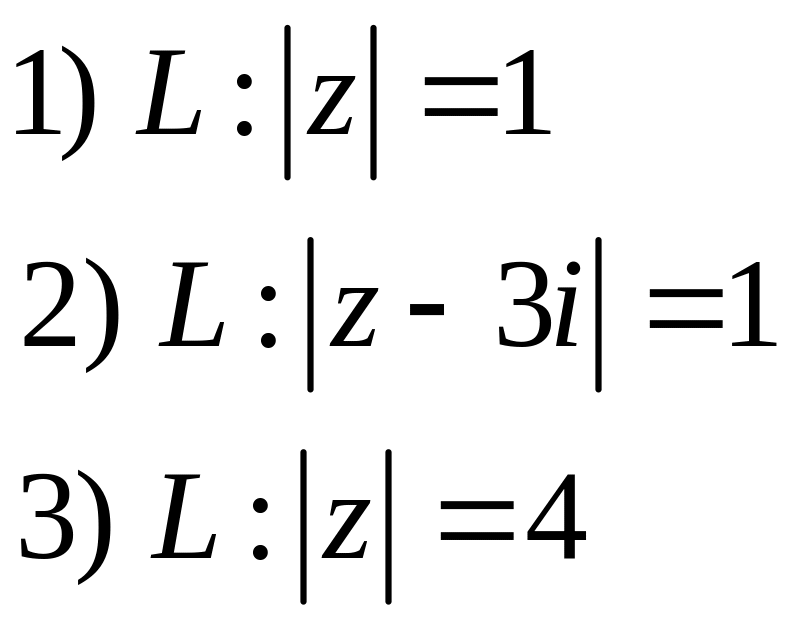
Решение

Теорема Коши о вычетах:

Если точка – есть полюс n-го порядка функции , то

В случае простого полюса

Знаменатель подынтегральной функции обращается в нуль в точках .

1) Внутри окружности подынтегральная функция аналитическая, поэтому в силу теоремы Коши:

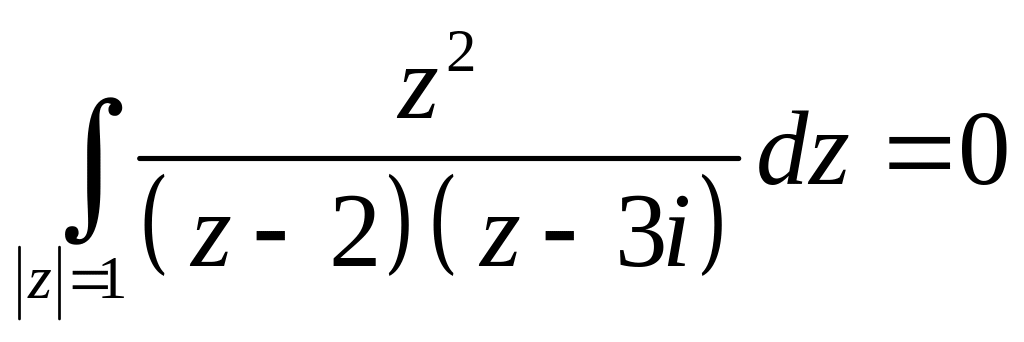
2) Внутри окружности функция имеет полюс первого порядка , согласно теореме Коши о вычетах:

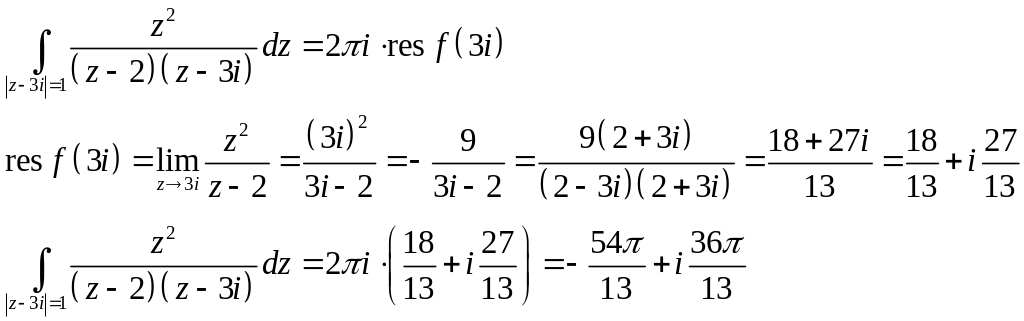
3) Внутри окружности функция имеет два полюса первого порядка и . Согласно теореме Коши о вычетах:

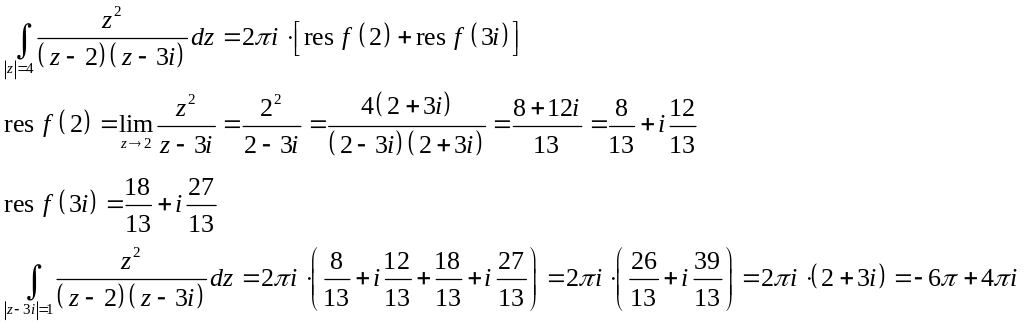
Операционное исчисление.

3.33 Найти оригинал изображения

.

Решение. Представляя изображение в виде 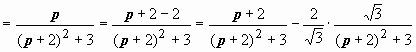и сравнивая эти выражения с формулами, находим оригинал .

3.34. Найти оригинал изображения

. .

Решение. Наличие степеней переменной р в знаменателе позволяет применить теорему об интегрировании оригинала: , , .

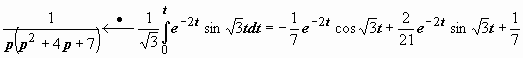Можно решить этот пример с помощью свёртки:

, . Однако проще всего представить F(p) в виде суммы простых дробей

3.35. Найти решение задачи Коши методами операционного исчисления x″ − 2 x′ + x = e ^t,   x(0) = 1,   x′(0) = 2.  Решение. Пусть x(t) X(p).

Тогда x ′(t) p X(p) − x(0) = p X(p) − 1,

x ″(t) p² X(p) − p − 2,

, и изображение задачи имеет вид .

Находим X(p): . Обращаем это изображение: , 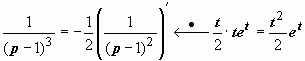. Решение задачи: .

3.36 Найти решение системы

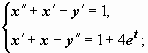
удовлетворяющее условиям: x(0) = 1,    x′(0) = 2,    y(0) = 0,    y′(0) = 1 при t = 0. Решение. Пусть x(t) X(p),  y(t) Y(p).

Тогда  x′(t) p X(p) − 1,  y′(t) p Y(p), 

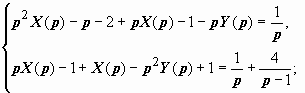
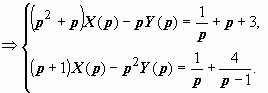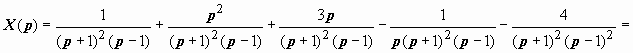
 x″(t) p ²X(p) − p − 2,  y″(t) p ²Y(p) − 1, и изображение задачи имеет вид         Решаем эту систему относительно X( p), Y( p): из первого уравнения вычитаем второе, умноженное на р: (после разложения на простые дроби) ;         Если на р умножить первое уравнение и вычесть второе, получим . Итак, решение задачи .