
Тренировочные упражнения математика 3 сем
ИВТ
2012-2013
Модуль 1 Кратные, криволинейные интегралы
Кратные интегралы.
1.1. Вычислить
![]() ,
,
где область
![]() ограничена прямыми
ограничена прямыми
![]()
Решим пример двумя способами.
|
Первый способ.
Выполним внутреннее интегрирование
по
Вычислим внутренний интеграл: |
|
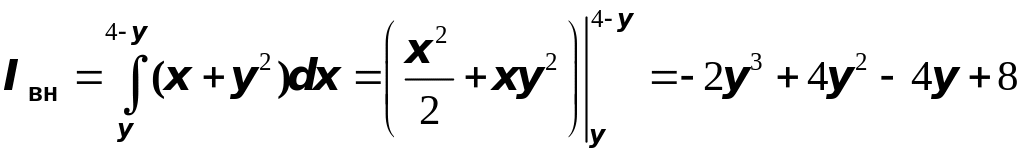 .
.
Подставляя найденное
значение в выражение для
![]() ,
получим
,
получим
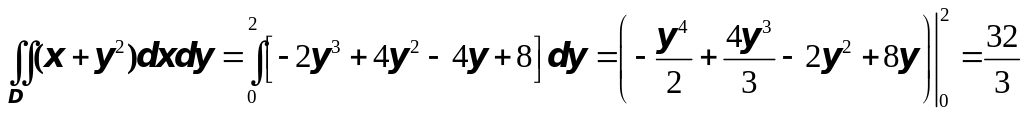 .
.
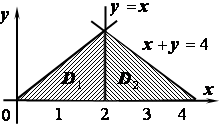
Второй способ.
Внутреннее
интегрирование выполним по переменной
,
а внешнее - по переменной
.
Заметим, что при этом область
мы должны разбить на две области
![]() и
и
![]() , следовательно, двойной интеграл
выразится в виде суммы таких двух
повторных интегралов:
, следовательно, двойной интеграл
выразится в виде суммы таких двух
повторных интегралов:
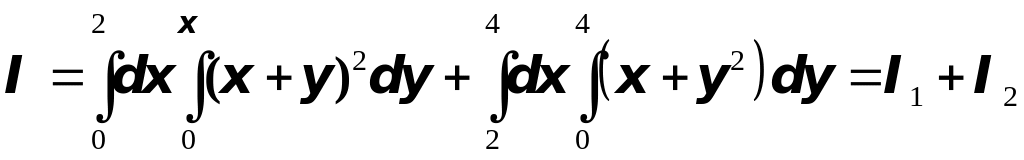
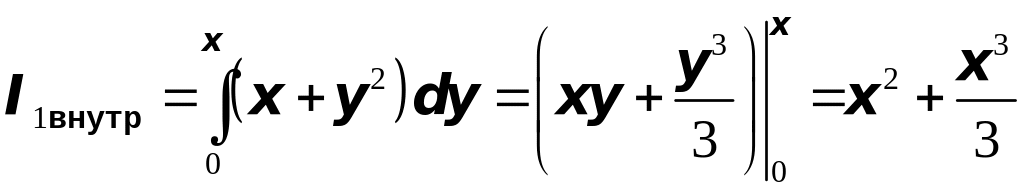
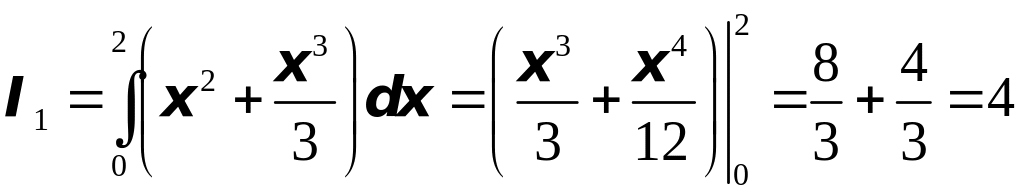
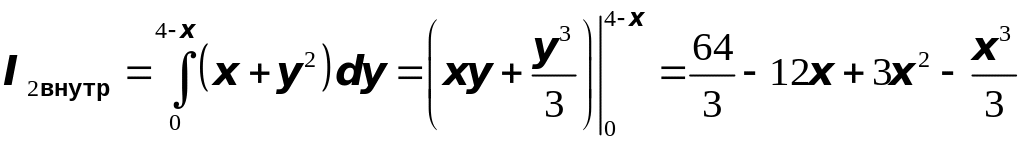
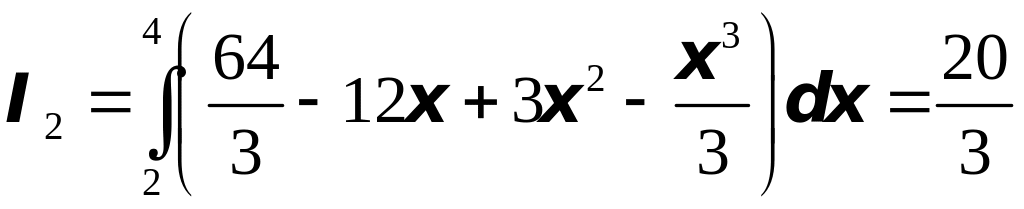
Итак, окончательно
получим
![]() .
.
1.2.
Вычислить объём тела, ограниченного
координатными плоскостями и плоскостью
![]()
![]() .
.
Искомый объём
![]() ,
где тело
,
где тело
![]() есть пирамида, ограниченная плоскостью
есть пирамида, ограниченная плоскостью
![]() и координатными плоскостями.
и координатными плоскостями.
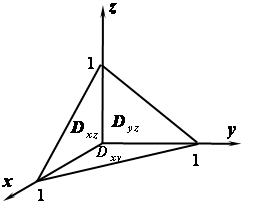
Очевидно, что этот тройной интеграл можно выразить шестью различными способами через трёхкратный:
|
или
|
|
Проведём вычисления по последней формуле, получим
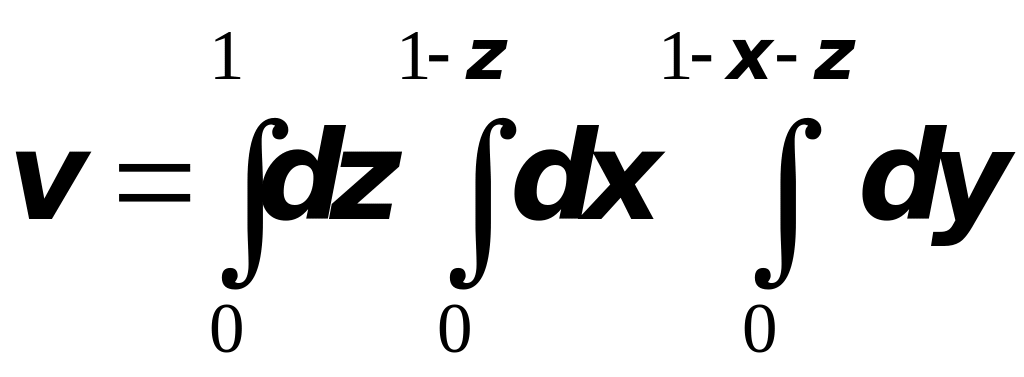 .
.
Имеем
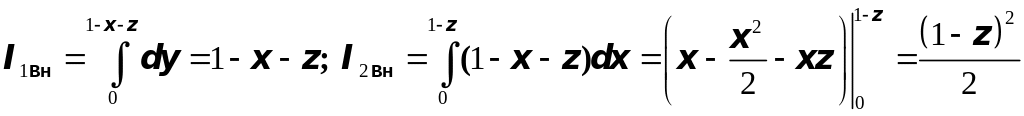 .
.
Наконец,
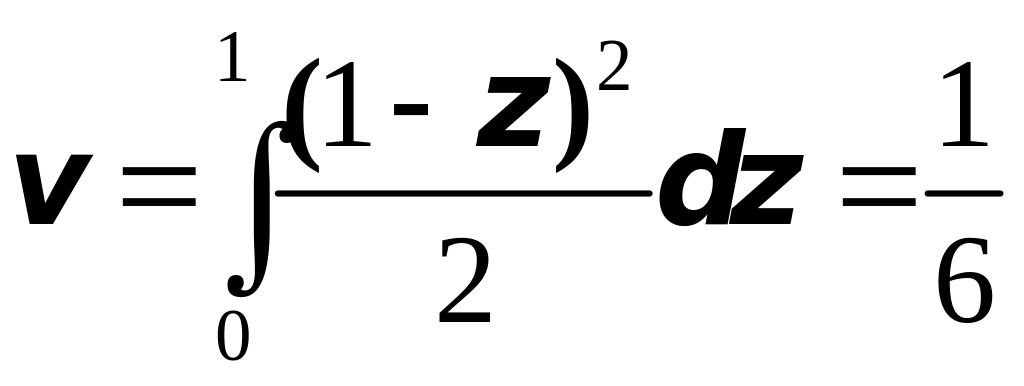 куб. ед.
куб. ед.
1.3. Найти
часть площади поверхности цилиндра
![]() ,
вырезанной из него плоскостями
,
вырезанной из него плоскостями
![]()
Решение.
|
Цилиндр
имеет образующую, параллельную оси
|
|
Проекция этой
части на плоскость
![]() представляет собой треугольник
представляет собой треугольник
![]() ,
который и является областью интегрирования.
При переходе к повторному интегралу
надо вести внутреннее интегрирование
по
,
который и является областью интегрирования.
При переходе к повторному интегралу
надо вести внутреннее интегрирование
по
![]() ,
а внешнее по
,
а внешнее по
![]() .
Находим
.
Находим
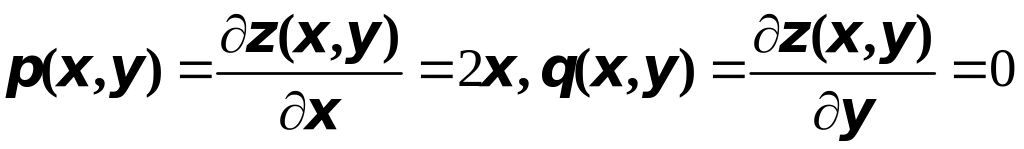 .
.
Вычисляем площадь поверхности:
![]()
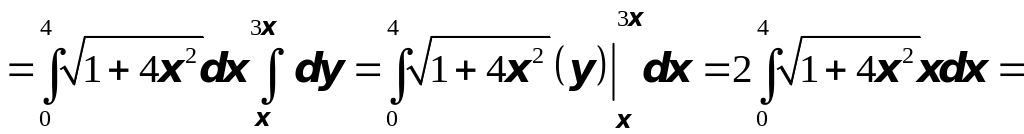
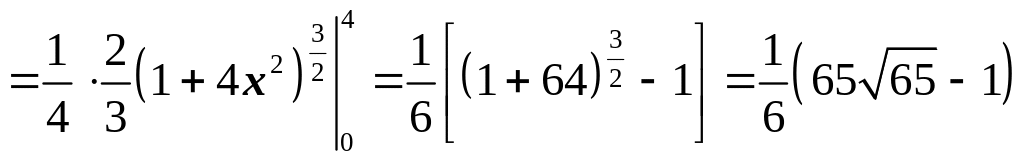 .
.
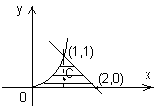
1.4. Найти
центр тяжести однородной пластинки,
ограниченной линиями
![]()
Решение. Находим
массу, которая при
![]() численно равна площади:
численно равна площади:
|
|
|
Находим статические моменты пластинки:
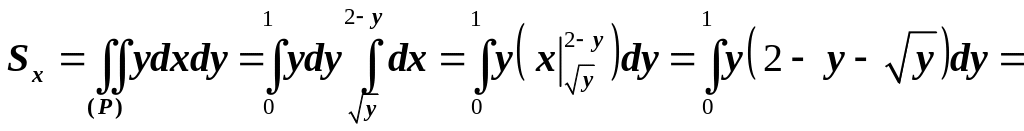
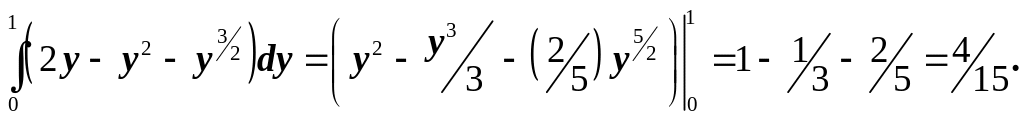
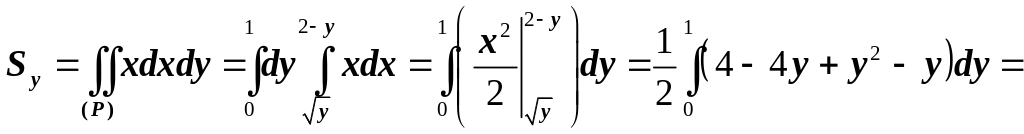
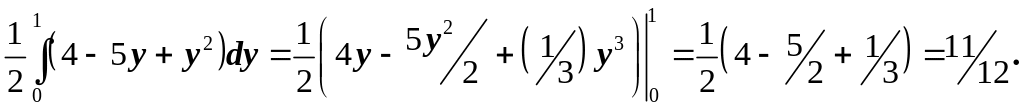
Итак, центр тяжести имеет координаты:
![]() .
.
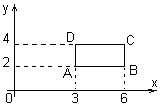
Положение центра
тяжести
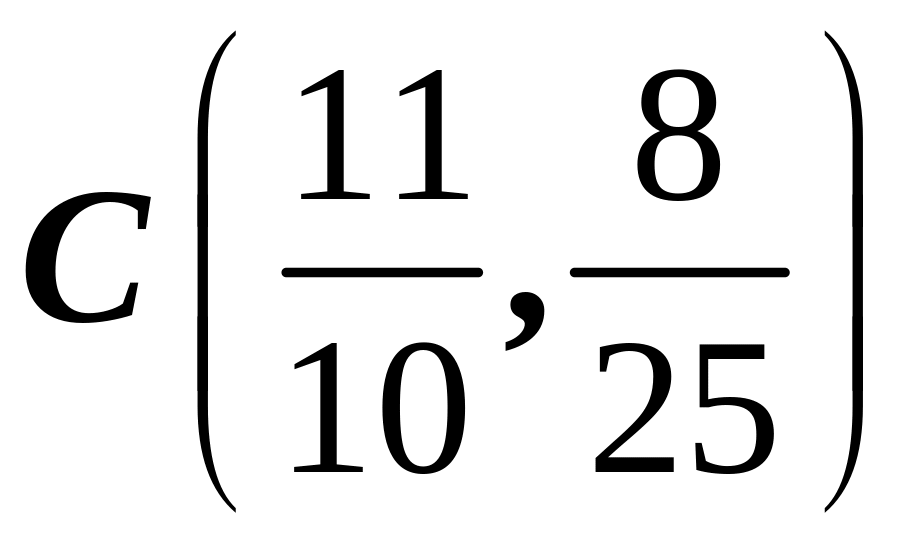 помечено на рисунке.
помечено на рисунке.
1.5. Вычислить
![]() ,
где
есть круг
,
где
есть круг
![]()
Решение.
Перейдём к полярным координатам
![]() .
В полярных координатах уравнение
окружности
.
В полярных координатах уравнение
окружности
![]() при любом
при любом
![]() (т.е.
меняется от
(т.е.
меняется от
![]() до 2
до 2![]() ),
а
),
а
![]() является постоянным,
является постоянным,
![]() ,
тогда получим
,
тогда получим
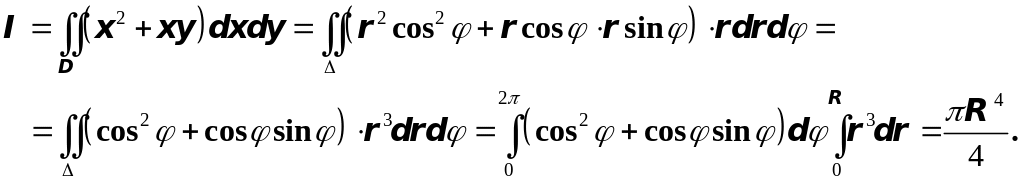
Для того, чтобы расставить пределы интегрирования, достаточно выяснить, как проходят (возрастают) через область координатные линии и .
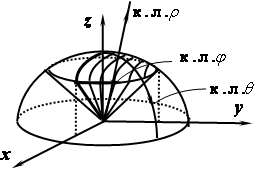
1.6. Найти
объём тела, лежащего в первом октанте
и ограниченного снизу конической
поверхностью
![]() ,
сверху шаровой поверхностью
,
сверху шаровой поверхностью
![]() ,
а с боков координатными плоскостями
,
а с боков координатными плоскостями
![]() и
и
![]() .
.
Решение. Искомый объём . Перейдём к сферическим координатам
|
Найдём уравнения конуса в сферических координатах:
|
|
откуда
следует
![]() и
и
![]() .
Заметим, верхняя чаша конуса имеет
уравнение
,
а нижняя
.
Нетрудно убедиться, что уравнение
шаровой поверхности
в сферических координатах
.
Итак, искомый объём
.
Заметим, верхняя чаша конуса имеет
уравнение
,
а нижняя
.
Нетрудно убедиться, что уравнение
шаровой поверхности
в сферических координатах
.
Итак, искомый объём
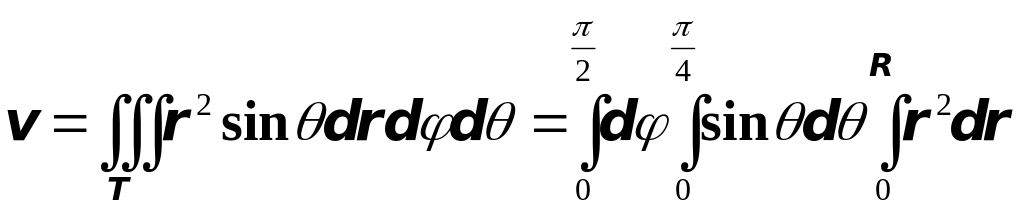 .
.
Вычислим
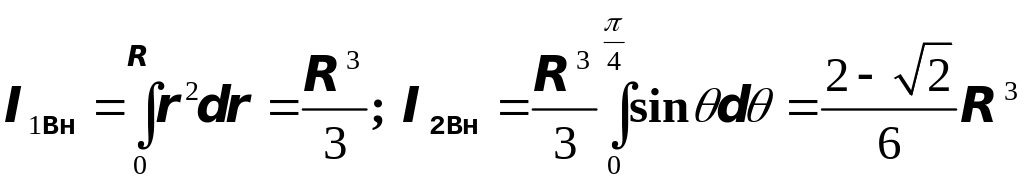 .
.
Окончательно
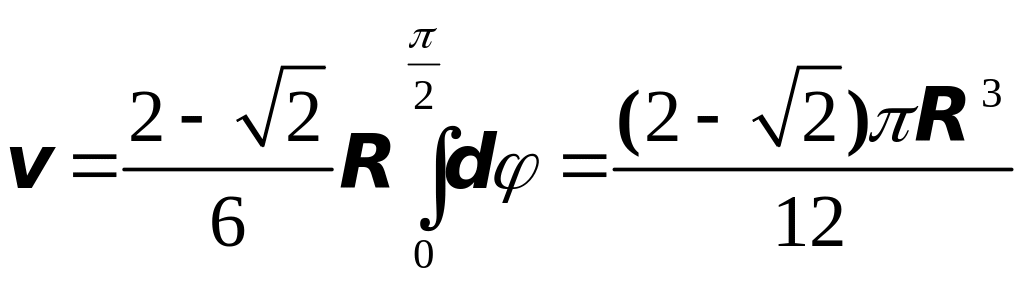 куб. ед.
куб. ед.
Криволинейные интегралы.
1.7.
Вычислить криволинейный интеграл
![]() ,
где
,
где
![]() –
дуга кривой
–
дуга кривой
![]() между точками, для которых
между точками, для которых
![]() .
.
Решение.
Поскольку
![]() ,
,
![]() и на дуге кривой
функция
и на дуге кривой
функция
![]() ,
,
по формуле
![]()
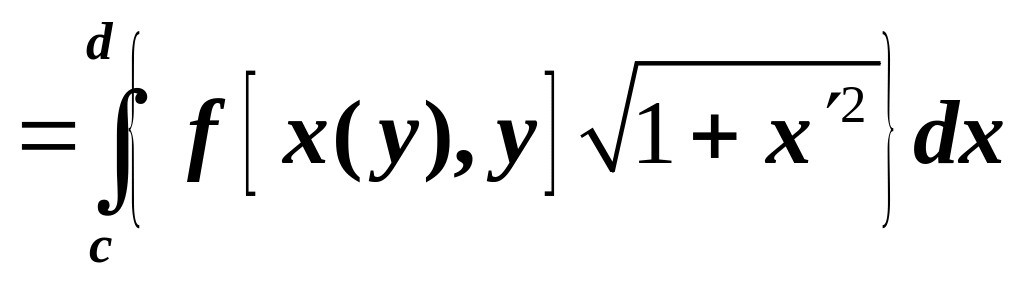 находим
находим
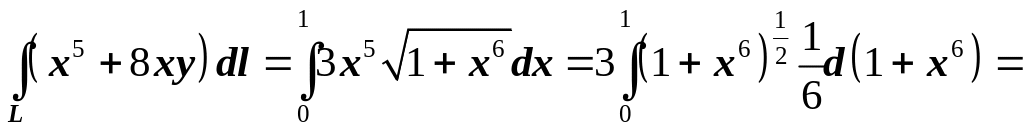
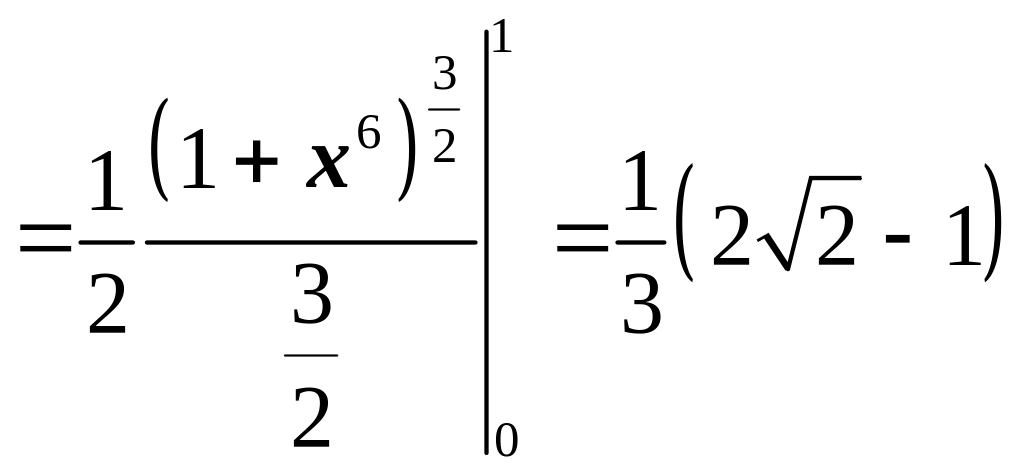 .
.
1.8.
Вычислить
интеграл
![]() по одному витку винтовой линии
по одному витку винтовой линии
![]()
Решение:
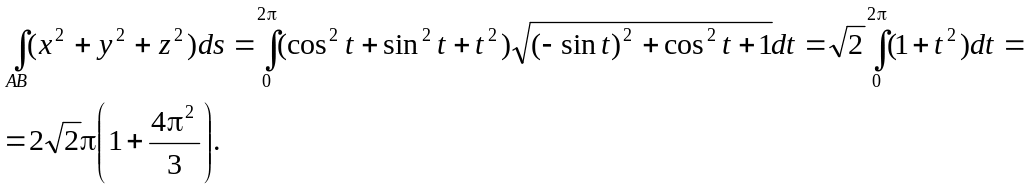
1.9.
Вычислить
![]() ,
где
–
отрезок прямой между точками
,
где
–
отрезок прямой между точками
![]() .
.
Решение. Составим уравнение прямой, проходящей через точки :
![]() ,
или
,
или
![]() .
.
Таким образом, получаем параметрическое уравнение прямой:
![]() .
.
Точка М пробегает
отрезок М1М2
, когда
![]() изменяется от 0 до 1. Так как
изменяется от 0 до 1. Так как
![]() .
.
По формуле
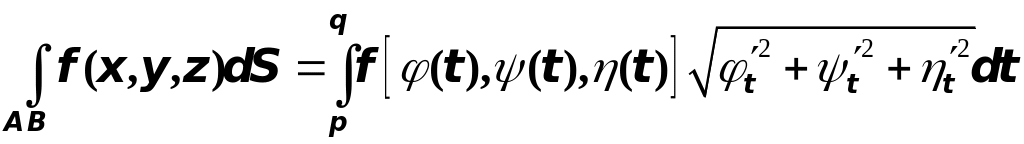 находим
находим
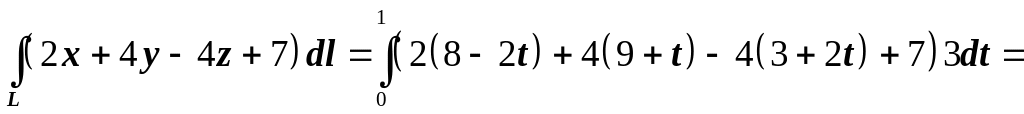
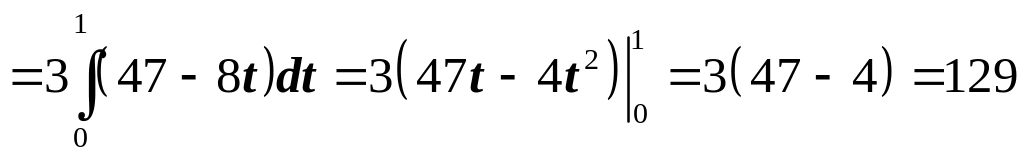 .
.
1.10
Вычислить
криволинейный интеграл
![]() .
L
– контур, ограниченный параболами
.
L
– контур, ограниченный параболами
![]() .
Направление обхода контура положительное.
.
Направление обхода контура положительное.
Решение:
1 способ
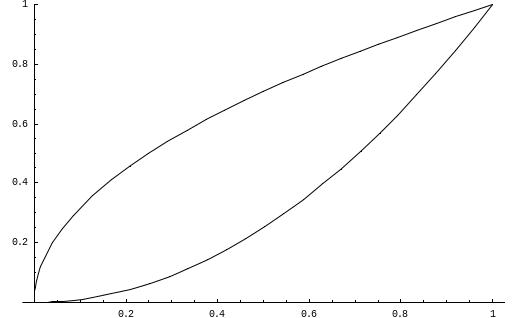


Представим
замкнутый контур L
как сумму двух дуг L1
= x2
и
![]()
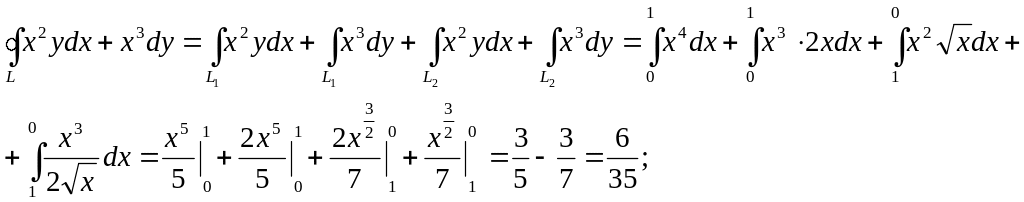
2 способ.
Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.
Решение:
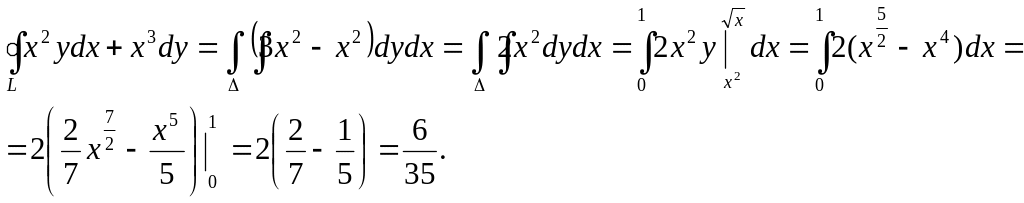
1.11
Вычислить криволинейный интеграл
![]() ,
если кривая АВ задана уравнением
,
если кривая АВ задана уравнением
![]() и
и
![]() .
.
Решение. Так
как кривая задана явным уравнением вида
![]() ,
то используем формулу
,
то используем формулу
![]()
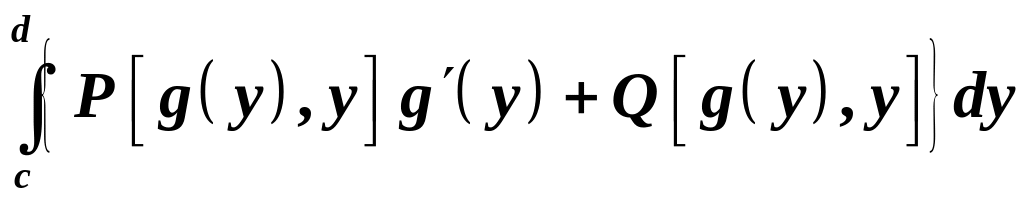 .
.
Находим
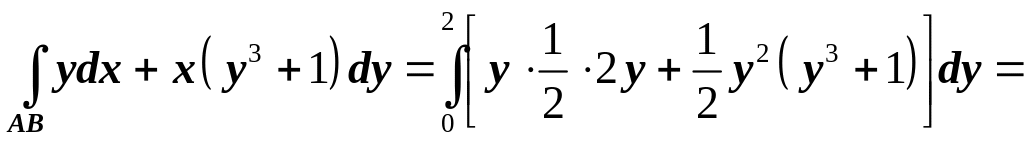
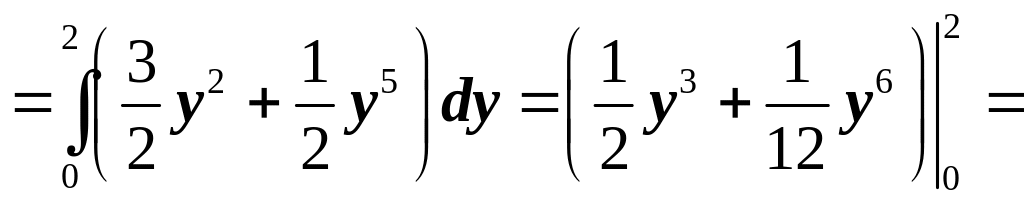
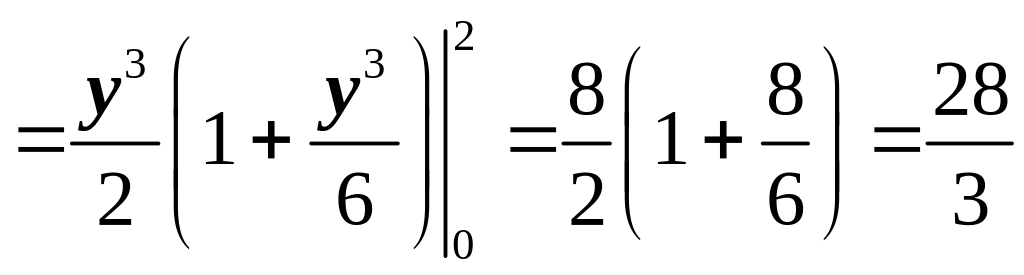 .
.
1.12
Вычислить криволинейный интеграл
![]() ,
если кривая АВ задана уравнениями
,
если кривая АВ задана уравнениями
![]() и
и
![]() .
.
Решение. Кривая есть часть эллипса с полуосями 3 и 2, находящаяся в первой четверти.
Используя формулу
![]()
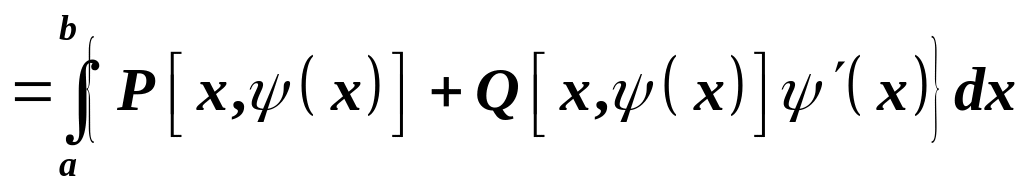 ,
находим:
,
находим:

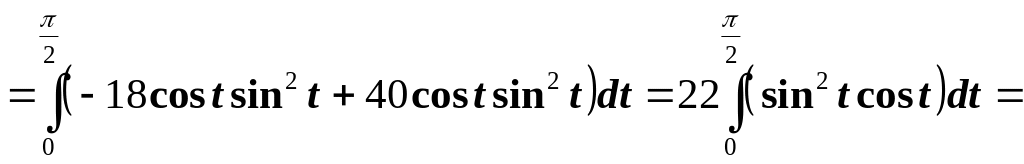
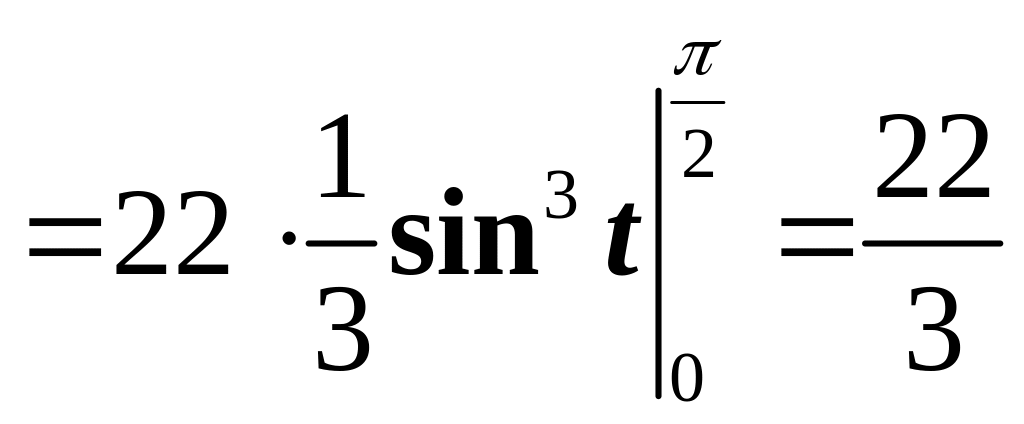 .
.
1.13
С помощью формулы Грина вычислить
криволинейный интеграл второго рода
![]() ,
где
–
контур прямоугольника с вершинами
,
где
–
контур прямоугольника с вершинами
![]() .
Преобразуем этот интеграл по формуле
Грина
.
Преобразуем этот интеграл по формуле
Грина
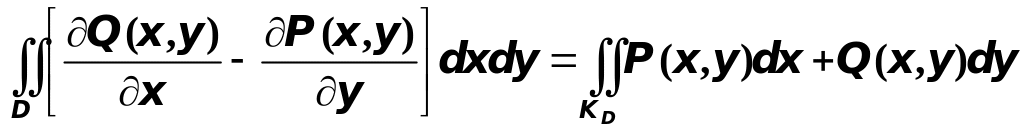 .
.
|
|
|
Тогда
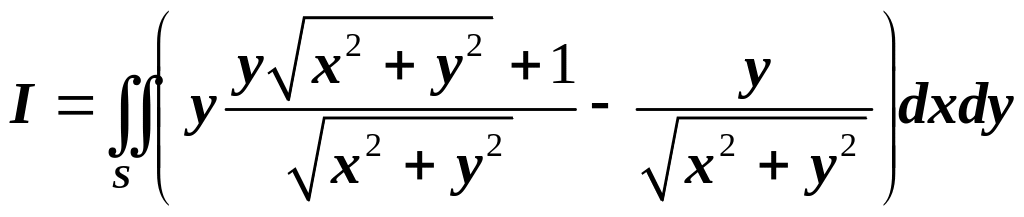
![]() ,
где область
,
где область
![]() ограничена контуром
,
в данном случае - прямоугольником
ограничена контуром
,
в данном случае - прямоугольником
![]() .
.
Вычисляем полученный двойной интеграл по прямоугольнику :
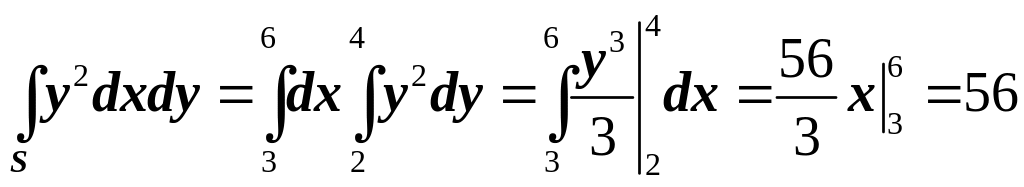 .
.
1.14 Вычислить
криволинейный интеграл второго рода
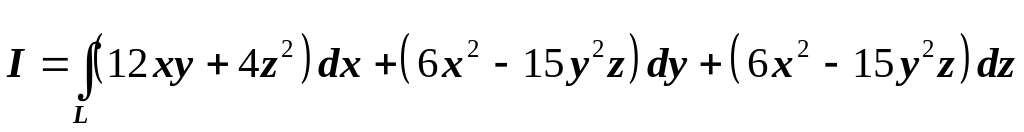 по пути интегрирования
с началом в точке
по пути интегрирования
с началом в точке
![]() и концом в точке
и концом в точке
![]() ,
предварительно установив, что он не
зависит от пути интегрирования.
,
предварительно установив, что он не
зависит от пути интегрирования.
Для данного
интеграла
![]() .
.
Так как
![]() ,
то условия формулы
,
то условия формулы
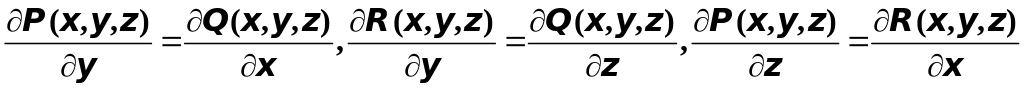
выполнены, т.е.
![]() .
.
Следовательно,
интеграл не зависит от пути интегрирования.
Вычислим его по отрезку прямой, проходящей
через точки
![]() и
и
![]() .
Параметрическое уравнение прямой имеет
вид
.
Параметрическое уравнение прямой имеет
вид
![]() ,
поэтому
,
поэтому
![]() .
На отрезке
.
На отрезке
![]()
![]() ,
то
,
то
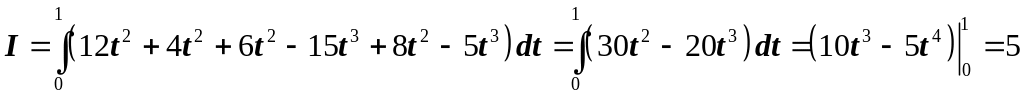 .
.

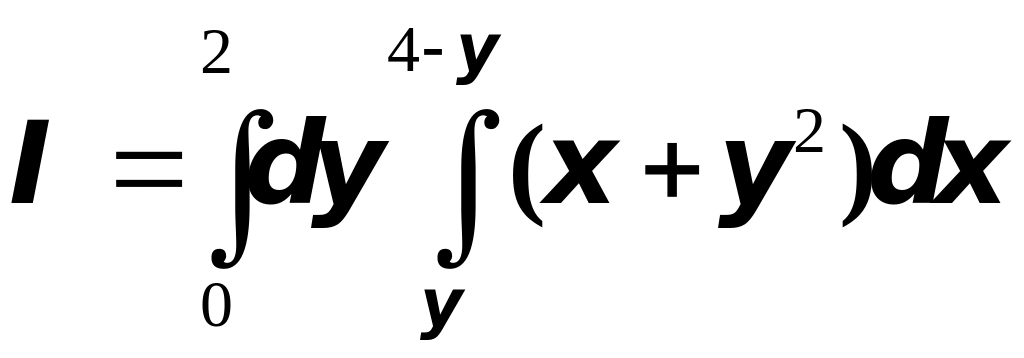 .
.
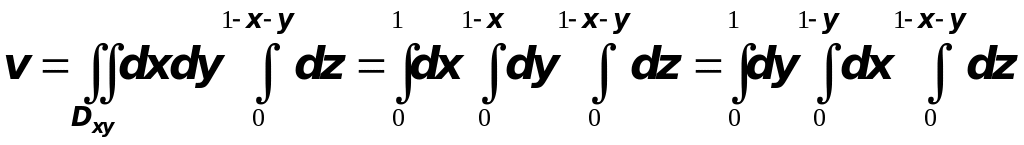
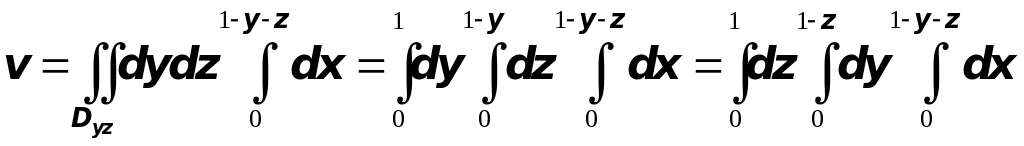 или
или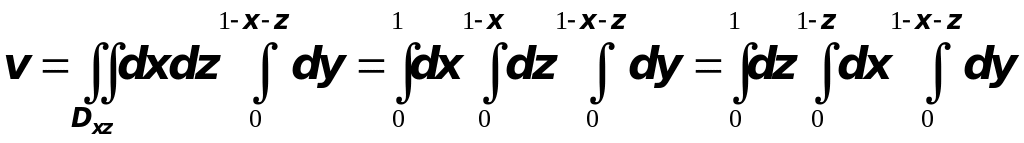
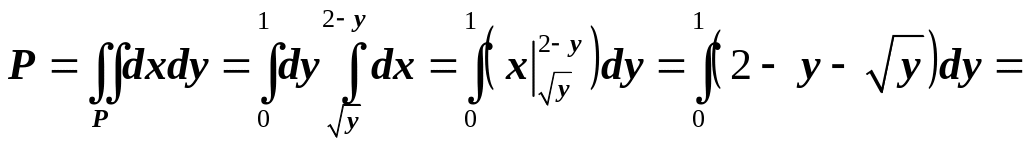
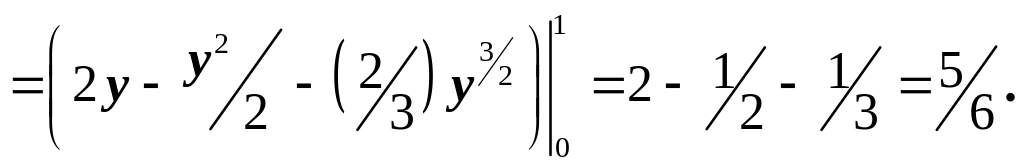
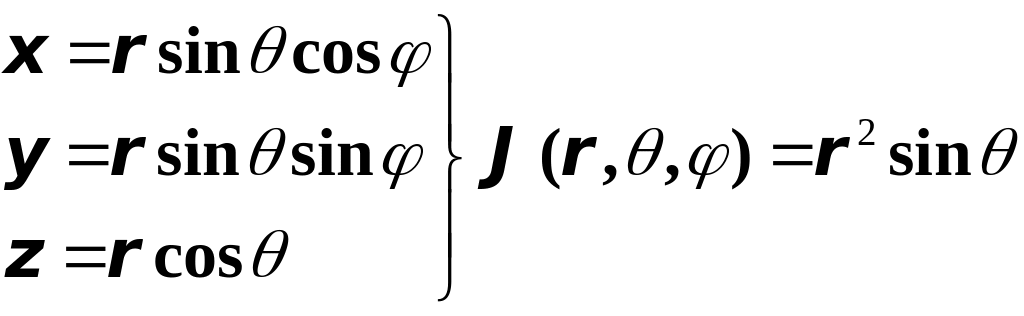
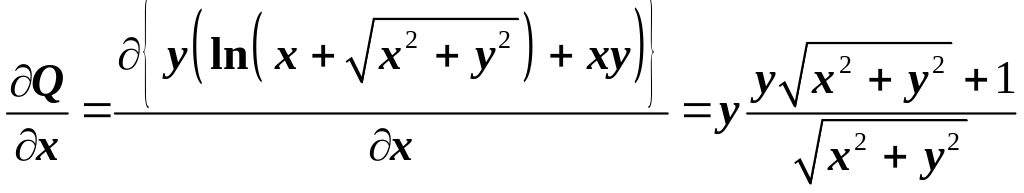 ,
,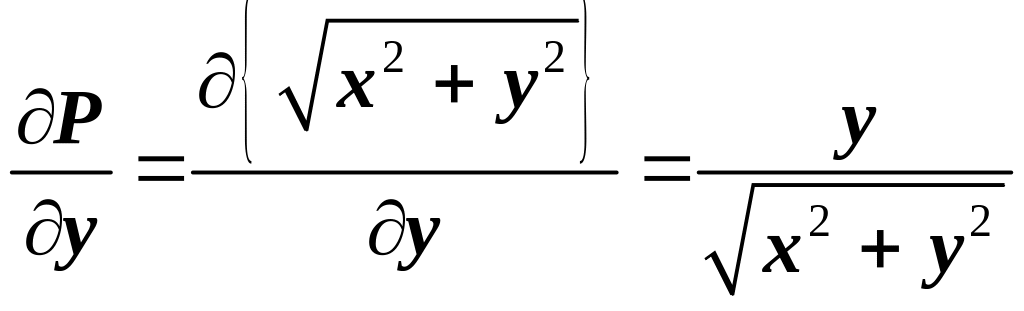 .
.