
- •Розділ 2. Функції
- •2.2. Способи задання функції
- •2.3. Область визначення та множина значень функції, заданої
- •2.4. Деякі властивості функцій
- •2.5. Асимптоти
- •2.7. Параметрично задані функції
- •2.8. Обернені функції
- •2.9. Складна функція
- •2.10. Класифікація функцій. Елементарні функції
- •2.10.1. Основні елементарні функції
- •2.11. Побудова графіків складних функцій методом перетворення
- •2.12. Функціональні моделі в економіці
- •2.12.1. Попит і пропозиції. Рівновага попиту і пропозицій
- •2.12.2. Функції загальних витрат, повного доходу та прибутку
- •2.12.4. Залежність величини попиту від доходу. Функції Торнквіста
- •2.12.5. Функція корисності, крива байдужості і лінія бюджетного
- •Запитання і завдання для самоперевірки
- •Завдання для самостійної роботи
2.12.4. Залежність величини попиту від доходу. Функції Торнквіста
Функції Торнквіста моделюють залежність попиту S від величини доходу (прибутку) I на:
а)
малоцінні товари
![]() ;
;
б)
товари першої необхідності
![]() ;
;
в)
товари другої необхідності
![]() ;
;
г)
товари розкоші
![]() ,
,
де
![]() – рівні доходів,
– рівні доходів,
![]() – рівень насичення,
– рівень насичення,
![]() .
.
На рис. 38 наведено графіки відповідних залежностей при:
а)
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ,
,
в
г)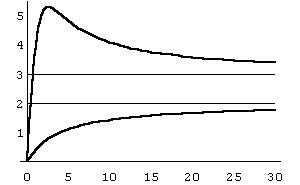
![]() ,
,
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() ,
,
![]() .
.
а)
в)
Р
б)
І
ф)
2.12.5. Функція корисності, крива байдужості і лінія бюджетного
обмеження
У теорії споживчого попиту на два блага x і y (наприклад, досліджуваного x і всіх інших y) корисність споживача може мати кількісний вимір, тобто визначатися функціонально.
Функція корисності показує залежність корисності від загальної кількості споживаних благ
![]() ,
,
де U – рівень корисності; х, у – кількість споживаних благ.
Крива
байдужості (ізокванта) –
це лінія рівної корисності, усі точки
якої характеризують набори благ x
і y, які забезпечують
споживачу один і той же рівень корисності
![]() .
Форма кривих байдужості залежить від
властивостей благ щодо замінюваності
у споживанні. Більшість благ є неповними
замінниками, а відповідні криві байдужості
є монотонно спадними функціями.
.
Форма кривих байдужості залежить від
властивостей благ щодо замінюваності
у споживанні. Більшість благ є неповними
замінниками, а відповідні криві байдужості
є монотонно спадними функціями.
Рис.39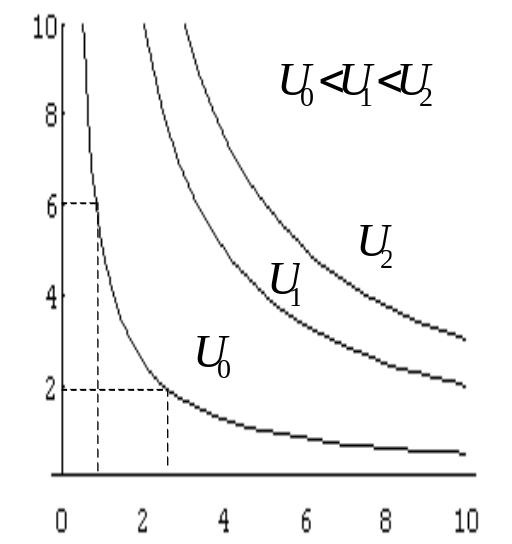
![]() ,
для якої крива байдужості має вигляд
,
для якої крива байдужості має вигляд
![]() .
Характерні графіки таких кривих
байдужості наведено на рис. 39. Із рис.39
видно, що криві байдужості даного типу
вигнуті до початку координат, не
перетинаються і мають асимптотами
осі координат. Крім того, криві
байдужості, які лежать далі від початку
координат, характеризують набори
благ, що мають вищий рівень корисності.
Зокрема, для наведених на рис.39 кривих
байдужості
.
Характерні графіки таких кривих
байдужості наведено на рис. 39. Із рис.39
видно, що криві байдужості даного типу
вигнуті до початку координат, не
перетинаються і мають асимптотами
осі координат. Крім того, криві
байдужості, які лежать далі від початку
координат, характеризують набори
благ, що мають вищий рівень корисності.
Зокрема, для наведених на рис.39 кривих
байдужості
![]() .
.
Для зручності геометричної інтерпретації розглянемо випадок, коли споживач повністю витрачає весь свій дохід І на придбання тільки двох благ (товарів) x і y. Тоді бюджетне обмеження буде мати вигляд
![]() ,
,
д
Рис.40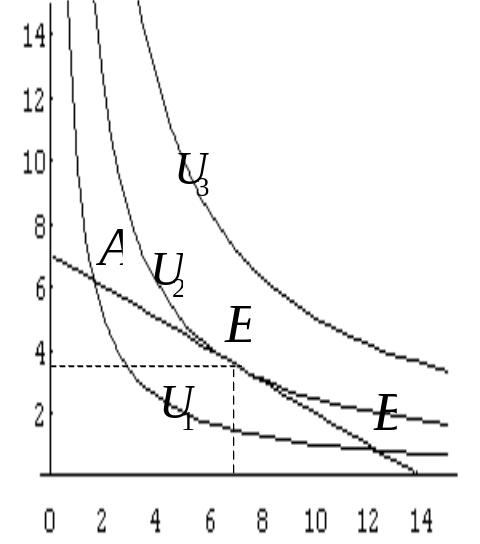
![]() – ціни відповідних благ. Графіком
бюджетного обмеження є пряма лінія, яку
можна представити рівнянням прямої у
відрізках
– ціни відповідних благ. Графіком
бюджетного обмеження є пряма лінія, яку
можна представити рівнянням прямої у
відрізках
![]() ,
де
,
де
![]() ,
,
![]() – максимальна кількість благ, які можна
придбати відповідно за ціною
– максимальна кількість благ, які можна
придбати відповідно за ціною
![]() або
або
![]() ,
якщо на придбання кожного з них витратити
весь дохід І (рис.40 ).
,
якщо на придбання кожного з них витратити
весь дохід І (рис.40 ).
Будемо
вважати, що кожний споживач у межах
бюджетних обмежень старається розподілити
свій дохід між різними споживчими
благами так, щоб максимізувати корисність
![]() .
Відповідний набір благ називається
оптимальним планом споживання або
станом рівноваги споживача.
Зрозуміло, що певні набори благ при
заданому бюджетному обмежені недосяжні
споживачеві (крива байдужості
.
Відповідний набір благ називається
оптимальним планом споживання або
станом рівноваги споживача.
Зрозуміло, що певні набори благ при
заданому бюджетному обмежені недосяжні
споживачеві (крива байдужості
![]() ),
тому що розташовані за межами його
бюджетних можливостей. Точки А і В
на кривій байдужості
),
тому що розташовані за межами його
бюджетних можливостей. Точки А і В
на кривій байдужості
![]() не можуть забезпечити максимізацію
корисності, бо при своєму доході споживач
має змогу забезпечити вищий рівень
корисності, перебуваючи на максимальній
кривій байдужості. Максимальна корисність
досягається у точці Е, де лінія
бюджетного обмеження дотична до кривої
байдужості
не можуть забезпечити максимізацію
корисності, бо при своєму доході споживач
має змогу забезпечити вищий рівень
корисності, перебуваючи на максимальній
кривій байдужості. Максимальна корисність
досягається у точці Е, де лінія
бюджетного обмеження дотична до кривої
байдужості
![]() .
.
