
- •Розділ 2. Функції
- •2.2. Способи задання функції
- •2.3. Область визначення та множина значень функції, заданої
- •2.4. Деякі властивості функцій
- •2.5. Асимптоти
- •2.7. Параметрично задані функції
- •2.8. Обернені функції
- •2.9. Складна функція
- •2.10. Класифікація функцій. Елементарні функції
- •2.10.1. Основні елементарні функції
- •2.11. Побудова графіків складних функцій методом перетворення
- •2.12. Функціональні моделі в економіці
- •2.12.1. Попит і пропозиції. Рівновага попиту і пропозицій
- •2.12.2. Функції загальних витрат, повного доходу та прибутку
- •2.12.4. Залежність величини попиту від доходу. Функції Торнквіста
- •2.12.5. Функція корисності, крива байдужості і лінія бюджетного
- •Запитання і завдання для самоперевірки
- •Завдання для самостійної роботи
2.11. Побудова графіків складних функцій методом перетворення
графіків базових функцій
Для
проведення дослідження функцій і
побудови їх графіків у більшості випадків
користуються похідною. Разом із тим
актуальним залишається метод, який
базується на перетворенні графіка
підходящої елементарної функції до
його збігання з графіком заданої функції.
Цим методом особливо зручно користуватись,
якщо задана функція може бути виражена
через одну з елементарних функцій у
вигляді
![]() .
Тоді графік заданої функції буде
комбінацією паралельних переміщень
(горизонтальних і вертикальних), а також
стиснень-розтягів (горизонтальних і
вертикальних) графіка відповідної
елементарної функції.
.
Тоді графік заданої функції буде
комбінацією паралельних переміщень
(горизонтальних і вертикальних), а також
стиснень-розтягів (горизонтальних і
вертикальних) графіка відповідної
елементарної функції.
Нехай
задано графік функції
![]() .
Тоді мають місце наступні перетворення.
.
Тоді мають місце наступні перетворення.
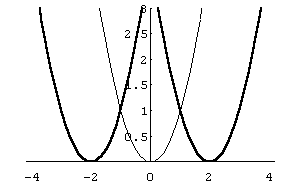
Горизонтальне переміщення
 .
Графік функції
.
Графік функції
 одержується
з графіка
функції
шляхом паралельного перенесення
(при
одержується
з графіка
функції
шляхом паралельного перенесення
(при
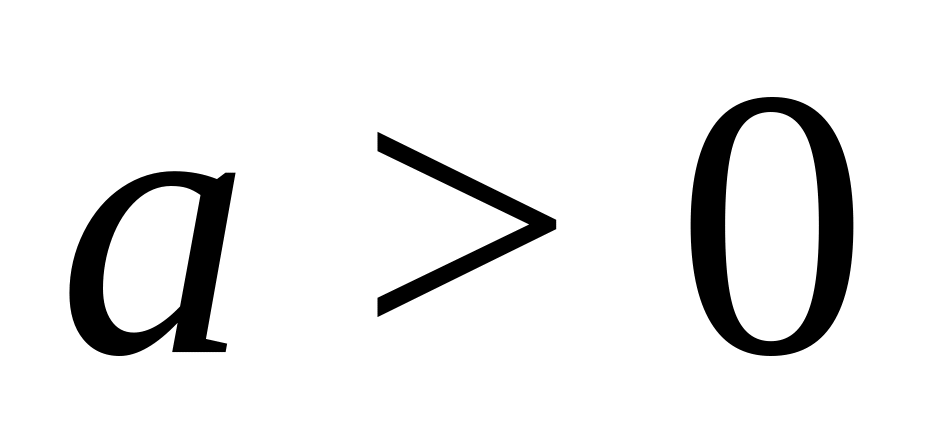 вліво,
вліво,
п
Рис. 24
Рис.
23
![]()
![]()
![]()
![]()
![]()
![]() вправо) на
вправо) на
![]() одиниць вздовж осі Ох
(рис. 23 ).
одиниць вздовж осі Ох
(рис. 23 ).
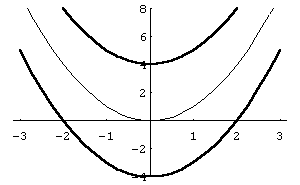
![]() вверх,
при
вверх,
при
![]() вниз) на
вниз) на
![]() одиниць вздовж осі
одиниць вздовж осі
![]() (рис. 24).
(рис. 24).
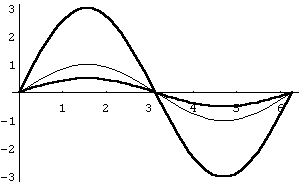
3.
Стиснення-розтяг
по осі ординат
![]() .
У даному
випадку графік функції
(
.
У даному
випадку графік функції
(![]() )
одержується з графіка функції
шляхом розтягу (при
)
одержується з графіка функції
шляхом розтягу (при
![]() )
або стиснення (при
)
або стиснення (при
![]() )
останнього в
)
останнього в
![]() разів вздовж
осі абсцис (рис. 25).
разів вздовж
осі абсцис (рис. 25).
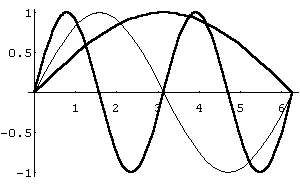
Рис. 25
Рис. 26
![]()
![]()
![]()



![]()
![]()
4.
Стиснення-розтяг
по осі абсцис
![]() .
У даному випадку графік функції
(
.
У даному випадку графік функції
(![]() )
одержується з графіка функції
шляхом стиснення (при
)
одержується з графіка функції
шляхом стиснення (при
![]() )
або розтягу (при
)
або розтягу (при
![]() )
останнього в
)
останнього в
![]() або, відповідно, в
або, відповідно, в
![]() разів уздовж
осі абсцис (рис. 26).
разів уздовж
осі абсцис (рис. 26).
5.
Дзеркальне
відображення.
У випадку, якщо
![]() ,
то кожному значенню незалежної змінної
буде відповідати протилежне за знаком
значення ординати
,
то кожному значенню незалежної змінної
буде відповідати протилежне за знаком
значення ординати
![]() .
Таким чином, графік нової функції буде
дзеркальним відображенням функції
відносно осі абсцис (рис. 27).
.
Таким чином, графік нової функції буде
дзеркальним відображенням функції
відносно осі абсцис (рис. 27).
У
випадку, якщо
![]() ,
то кожному значенню залежної змінної
у
буде відповідати протилежне за знаком
значення абсциси
.
Таким чином, графік нової функції буде
дзеркальним відображенням функції
відносно осі ординат (рис. 28).
,
то кожному значенню залежної змінної
у
буде відповідати протилежне за знаком
значення абсциси
.
Таким чином, графік нової функції буде
дзеркальним відображенням функції
відносно осі ординат (рис. 28).
Рис. 27
Рис. 28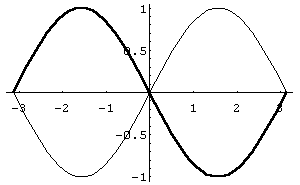
![]()
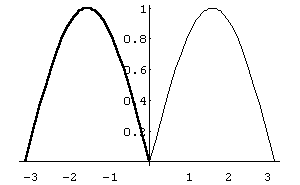
6.
Взяття модуля.
Нехай потрібно побудувати графік функції
![]() .
Якщо
.
Якщо
![]() ,
то
,
то
![]() ,
а отже, частину графіка, яка знаходиться
у верхній напівплощині, потрібно залишити
без зміни. Якщо
,
а отже, частину графіка, яка знаходиться
у верхній напівплощині, потрібно залишити
без зміни. Якщо
![]() ,
то
,
то
![]() ,
а це означає, що частину графіка, яка
знаходиться у нижній напівплощині,
потрібно дзеркально відобразити у
верхню напівплощину симетрично відносно
осі абсцис (рис. 29 ).
,
а це означає, що частину графіка, яка
знаходиться у нижній напівплощині,
потрібно дзеркально відобразити у
верхню напівплощину симетрично відносно
осі абсцис (рис. 29 ).
Н
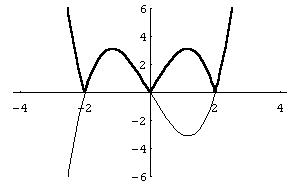
Рис. 30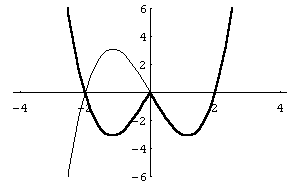
![]() .
Оскільки ця функція парна, то її графік
симетричний відносно осі ординат.
Оскільки для
.
Оскільки ця функція парна, то її графік
симетричний відносно осі ординат.
Оскільки для
![]()
![]() ,
то для
графіки
,
то для
графіки
![]() і
і
![]() співпадають. Таким чином, для побудови
графіка функції
потрібно частину графіка, яка знаходиться
у правій напівплощині, відобразити у
ліву напівплощину симетрично відносно
осі ординат (рис. 30).
співпадають. Таким чином, для побудови
графіка функції
потрібно частину графіка, яка знаходиться
у правій напівплощині, відобразити у
ліву напівплощину симетрично відносно
осі ординат (рис. 30).
Рис. 29
![]()
![]()
![]()
