
- •Розділ 2. Функції
- •2.2. Способи задання функції
- •2.3. Область визначення та множина значень функції, заданої
- •2.4. Деякі властивості функцій
- •2.5. Асимптоти
- •2.7. Параметрично задані функції
- •2.8. Обернені функції
- •2.9. Складна функція
- •2.10. Класифікація функцій. Елементарні функції
- •2.10.1. Основні елементарні функції
- •2.11. Побудова графіків складних функцій методом перетворення
- •2.12. Функціональні моделі в економіці
- •2.12.1. Попит і пропозиції. Рівновага попиту і пропозицій
- •2.12.2. Функції загальних витрат, повного доходу та прибутку
- •2.12.4. Залежність величини попиту від доходу. Функції Торнквіста
- •2.12.5. Функція корисності, крива байдужості і лінія бюджетного
- •Запитання і завдання для самоперевірки
- •Завдання для самостійної роботи
2.10. Класифікація функцій. Елементарні функції
2.10.1. Основні елементарні функції
До основних елементарних функцій відносяться:
Степенева функція
 ,
де
,
де
 – дійсне число;
– дійсне число;Показникова функція
 ,
де
,
де
 ;
;Логарифмічна функція
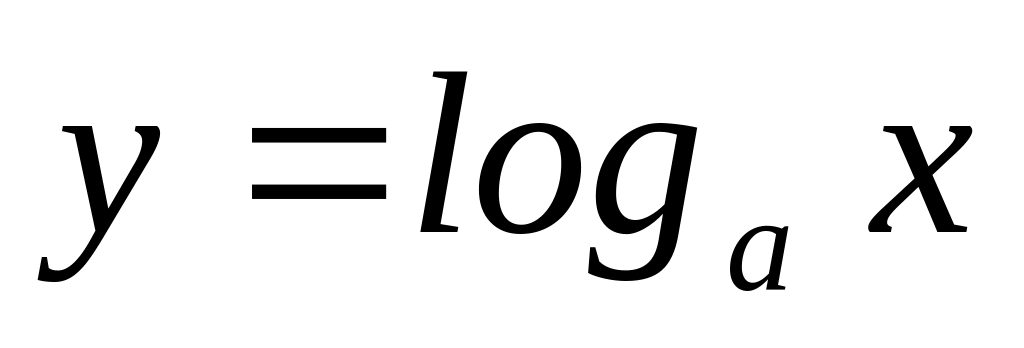 ,
де
;
,
де
;Тригонометричні функції:
 ;
;Обернені тригонометричні функції:

 ;
;
1.Степенева
функція
![]() .
Розглянемо
окремі випадки степеневої функції:
.
Розглянемо
окремі випадки степеневої функції:
а)
Функція
![]() ,
де n
– натуральне число. Область визначення
функції
,
де n
– натуральне число. Область визначення
функції
![]() ,
а область значень
,
а область значень
![]() .
Функція парна. Спадна для
.
Функція парна. Спадна для
![]() і зростаюча для
і зростаюча для
![]() .
.
Графіки функцій при n=2
і n=4,
наведено на рис.4.
.
.
Графіки функцій при n=2
і n=4,
наведено на рис.4.
Функція
![]() ,
де n
– натуральне число. Область визначення
функції
,
а область значень
,
де n
– натуральне число. Область визначення
функції
,
а область значень
![]() .
Функція непарна. Зростаюча для
.
Функція непарна. Зростаюча для
![]() .
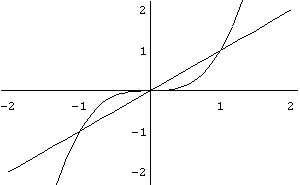
Графіки функцій при n=1
і n=3,
наведено на рис. 5.
.
Графіки функцій при n=1
і n=3,
наведено на рис. 5.
Рис.
4
Рис.
5



![]()

![]()
![]()
б)
Функція
![]() ,
де n
– натуральне число. Область визначення
функції
,
де n
– натуральне число. Область визначення
функції
![]() ,
а область значень
,
а область значень
![]() .
Функція непарна. Спадна для
.
Функція непарна. Спадна для
![]() .
.
Функція
![]() ,
де n
– натуральне число. Область визначення
функції
,
а область значень
,
де n
– натуральне число. Область визначення
функції
,
а область значень
![]() .
Функція парна. Зростаюча для
.
Функція парна. Зростаюча для
![]() і спадна для
і спадна для
![]() .
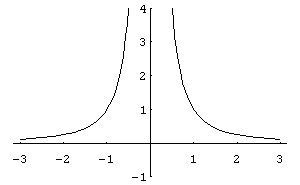
Графіки функцій при n=-1
і n=-2,
наведено на рис.6,7.
.
Графіки функцій при n=-1
і n=-2,
наведено на рис.6,7.
Рис.
6
Рис.
7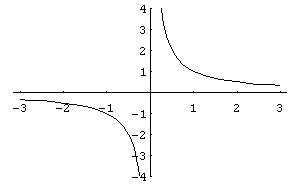
![]()
![]()
в)
Функція![]() ,
де
,
де
![]() – натуральне число. Область визначення
функції
– натуральне число. Область визначення
функції
![]() ,
а область значень
.
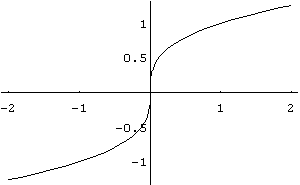
Функція зростаюча. Графік функції
,
а область значень
.
Функція зростаюча. Графік функції
![]() наведено на рис. 8.
наведено на рис. 8.
Функція![]() ,
де
– натуральне число. Область визначення
функції
,
а область значень
,
де
– натуральне число. Область визначення
функції
,
а область значень
![]() .
Функція зростаюча. Графік функції
.
Функція зростаюча. Графік функції
![]() наведено на рис. 9.
наведено на рис. 9.
Рис.
8
Рис.
9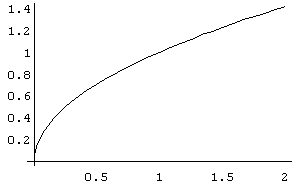
2
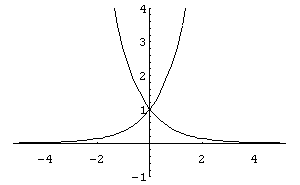
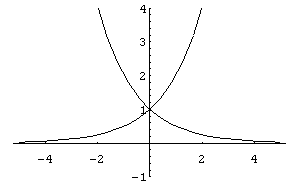
Рис.
11
Рис.
10
![]()
![]()
![]()
![]()
![]() .
Область визначення функції
уся множина дійсних чисел
,
а область значень
.
Якщо
.
Область визначення функції
уся множина дійсних чисел
,
а область значень
.
Якщо
![]() ,
то функція спадна, а якщо
,
то функція спадна, а якщо
![]() – функція зростаюча. Графіки окремих
функцій наведено на рис. 10,11.
– функція зростаюча. Графіки окремих
функцій наведено на рис. 10,11.
Показникова функція має широке застосування в економіці, зокрема, в математиці фінансів у формулі складних відсотків
![]() ,
,
де
Р
– початковий внесок, i
– відсоткова ставка, n
– кількість періодів (незалежна змінна),
![]() – значення внеску після n
періодів нарахування (залежна змінна).
– значення внеску після n
періодів нарахування (залежна змінна).
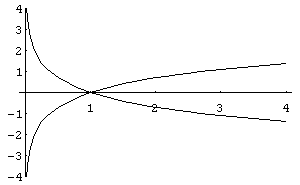
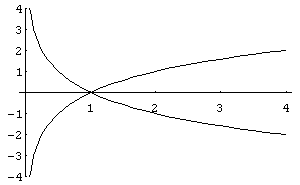
3.
Логарифмічна
функція
![]() .
Область
визначення функції
,
а область значень
.
Якщо
,
то функція спадна, а якщо
–
функція зростаюча. Графіки окремих
функцій наведено на рис.12,13.
.
Область
визначення функції
,
а область значень
.
Якщо
,
то функція спадна, а якщо
–
функція зростаюча. Графіки окремих
функцій наведено на рис.12,13.
Рис.
13
Рис.
12
![]()
![]()
![]()
![]()
4.
Тригонометричні функції
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
а)
Функції
та
визначені на
та мають область значень
![]() ,
періодичні з періодом
,
періодичні з періодом
![]() .
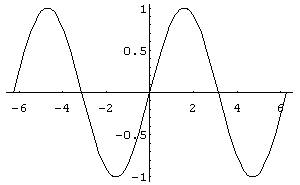
Функція
непарна, її графік
.
Функція
непарна, її графік
Рис.
14
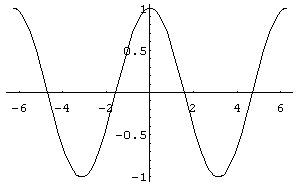
Рис.
15
![]()
![]()
(рис.14) симетричний відносно початку координат. Функція – парна, її графік (рис.15) симетричний відносно осі ординат.
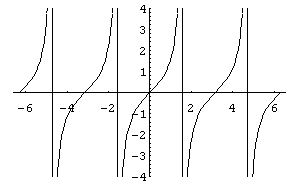
б)
Функція
визначена на всій дійсній осі, крім
![]() ,
монотонно зростаюча в кожному інтервалі
області визначення.
,
монотонно зростаюча в кожному інтервалі
області визначення.
Функція
визначена на всій дійсній осі, крім
![]() ,
монотонно спадна в кожному інтервалі
області визначення.
,
монотонно спадна в кожному інтервалі
області визначення.
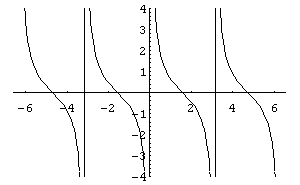
Функції
та
непарні,
симетричні відносно початку координат,
періодичні з періодом
![]() ,
область значень
,
область значень
![]() ,
їх графіки наведено відповідно на
рис.16,17.
,
їх графіки наведено відповідно на
рис.16,17.
Рис.
16
Рис.
17
![]()
![]()
5.
Обернені тригонометричні функції:
![]()
![]()
![]()
![]() .
.
Функція
![]() .
Оберненою тригонометричною функцією
називають дугу (кут) у,
із відрізка
.
Оберненою тригонометричною функцією
називають дугу (кут) у,
із відрізка
![]() ,
синус якої дорівнює х.
Іншими словами, рівності
і
,
синус якої дорівнює х.
Іншими словами, рівності
і
![]() еквівалентні. Аналогічно визначаються
інші обернені тригонометричні функції.
еквівалентні. Аналогічно визначаються
інші обернені тригонометричні функції.
Функція
визначена на
![]() та має область значень
та має область значень
![]() .
Монотонно зростаюча в області визначення,
непарна. Графік функції
наведено
на рис. 18.
.
Монотонно зростаюча в області визначення,
непарна. Графік функції
наведено
на рис. 18.
Ф
Рис. 18
Рис. 19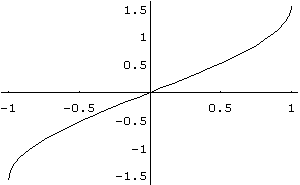
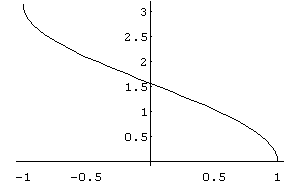
![]() визначена на
визначена на
![]() і має область значень
і має область значень
![]() .
Монотонно спадна в області визначення.
Для функції
має
місце
рівність
.
Монотонно спадна в області визначення.
Для функції
має
місце
рівність
![]() .
Графік функції
наведено
на рис. 19.
.
Графік функції
наведено
на рис. 19.
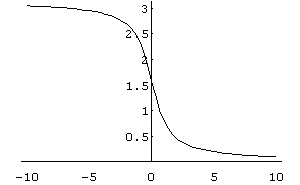
Функція
![]() визначена на
визначена на
![]() та має область значень
.
Монотонно зростаюча в області визначення,
непарна. Графік функції
наведено
на рис. 20.
та має область значень
.
Монотонно зростаюча в області визначення,
непарна. Графік функції
наведено
на рис. 20.
Функція
визначена на
та має область значень
![]() .
Функція монотонно спадна в області
визначення. Для функції
має
місце рівність
.
Функція монотонно спадна в області
визначення. Для функції
має
місце рівність
![]() .
Графік функції
наведено
на рис. 21.
.
Графік функції
наведено
на рис. 21.
Рис. 20
Рис. 21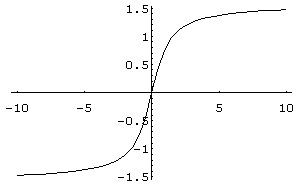
2.10.2. Елементарні функції
Функції, утворені з основних елементарних функцій та чисел із використанням арифметичних дій та операції взяття функції від функції (утворення складних функцій), називаються елементарними.
Найбільш типовими елементарними функціями, які мають застосування в економіці є цілі раціональні функції, дробово-раціональні функції та ірраціональні функції.
1. Цілі раціональні функції або поліноми (многочлени). У загальному вигляді поліноми записуються так:
![]() ,
,
де
y
і x
– відповідно залежна і незалежна змінні;
![]() – дійсні числа. При цьому
– дійсні числа. При цьому
![]() .
Число n
у цьому
випадку показує степінь поліноміальної
функції.
.
Число n
у цьому
випадку показує степінь поліноміальної
функції.
Якщо
n=1,
тоді маємо
![]() або
або
![]() – лінійну функцію.
– лінійну функцію.
Якщо
n=2,
тоді маємо
![]() або
або
![]() – квадратичну функцію.
– квадратичну функцію.
Якщо
n=3,
тоді маємо
![]() або
або
![]() – кубічну функцію.
– кубічну функцію.
При
n>1
поліном є нелінійною функцією. Із
нелінійних функцій найбільш широке
використання в економічних розрахунках
має квадратична функція
![]() .
.
Скориставшись методом виділення повного квадрату, квадратичну функцію можна подати у вигляді
![]() .
.
З
останньої рівності випливає, що графіком
квадратичної функції є парабола, вершина
якої знаходиться в точці
![]() ,
де
,
де
![]() ,
,
вітки
якої направлені вверх при
![]() і – вниз при
і – вниз при
![]() .
.
2. Дробово-раціональні функції. Дробово-раціональними функціями називаються функції, які можна подати у вигляді відношення двох поліномів:
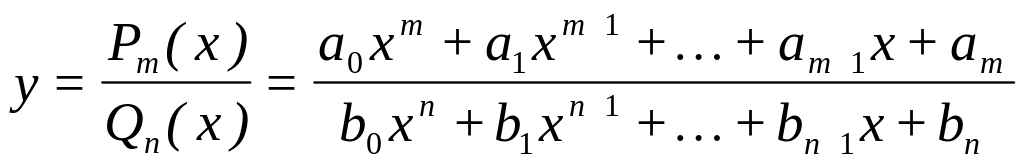 ,
,
де Pm(x) і Qn(x) деякі поліноміальні функції. Областю визначення поліноміальної функції є множина усіх дійсних чисел, крім тих точок, у яких знаменник перетворюється в нуль, тобто, крім тих значень змінної х, які є дійсними коренями рівняння Qn(x)=0.
Приклади
дробово-раціональних функцій:![]()
![]()
![]() .
.
Г
Рис. 22
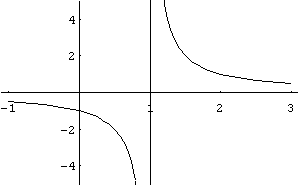
Наприклад,
функція
![]() має вертикальну асимптоту
.
Графік цієї функції подано на рис. 22.
Крім вертикальних асимптот
дробово-раціональна функція може
мати одну горизонтальну асимптоту y=b
або нахилену
асимптоту y=ax+b,
які характеризуються поведінкою функції
на нескінченності.
має вертикальну асимптоту
.
Графік цієї функції подано на рис. 22.
Крім вертикальних асимптот
дробово-раціональна функція може
мати одну горизонтальну асимптоту y=b
або нахилену
асимптоту y=ax+b,
які характеризуються поведінкою функції
на нескінченності.
Прикладом
дробово-раціональної функції може бути
математична модель вартості очистки
від забруднення цементом. Якщо p
відсоток очистки,
![]() ,
то вартість
очистки
атмосфери від забруднення цементом
складає величину
,
то вартість
очистки
атмосфери від забруднення цементом
складає величину
![]() .
.
Ця
раціональна функція має вертикальну
асимптоту
![]() і горизонтальну асимптоту
і горизонтальну асимптоту
![]() .
.
3. Ірраціональні функції. Функції, в яких, крім вище вказаних дій, використовується операція добування кореня, називаються ірраціональними. При цьому для кореня парного степеня враховується тільки його арифметичне значення.
Наприклад,
функції
![]() ,
,
![]() – ірраціональні.
– ірраціональні.
