
- •Розділ 2. Функції
- •2.2. Способи задання функції
- •2.3. Область визначення та множина значень функції, заданої
- •2.4. Деякі властивості функцій
- •2.5. Асимптоти
- •2.7. Параметрично задані функції
- •2.8. Обернені функції
- •2.9. Складна функція
- •2.10. Класифікація функцій. Елементарні функції
- •2.10.1. Основні елементарні функції
- •2.11. Побудова графіків складних функцій методом перетворення
- •2.12. Функціональні моделі в економіці
- •2.12.1. Попит і пропозиції. Рівновага попиту і пропозицій
- •2.12.2. Функції загальних витрат, повного доходу та прибутку
- •2.12.4. Залежність величини попиту від доходу. Функції Торнквіста
- •2.12.5. Функція корисності, крива байдужості і лінія бюджетного
- •Запитання і завдання для самоперевірки
- •Завдання для самостійної роботи
2.5. Асимптоти
Означення.
Асимптотою
графіка функції
![]() називається пряма, до якої як завгодно
близько наближається графік даної
функції, коли аргумент прямує до
нескінченності або до деякого числа у
випадку вертикальної асимптоти.
називається пряма, до якої як завгодно
близько наближається графік даної
функції, коли аргумент прямує до
нескінченності або до деякого числа у
випадку вертикальної асимптоти.
Асимптоти можуть бути вертикальними, нахиленими і горизонтальними.
Вертикальна
асимптота – це пряма
![]() ,
якщо
,
якщо
![]() .
.
Н
Рис. 3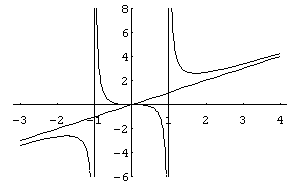
![]() ,
де коефіцієнт нахилу k
і коефіцієнт зміщення b
знаходяться шляхом обчислення границь:
,
де коефіцієнт нахилу k
і коефіцієнт зміщення b
знаходяться шляхом обчислення границь:
![]() ,
,
![]() .
Якщо
.
Якщо
![]() ,
то маємо горизонтальну асимптоту.
На рис. 3 наведено графік
функції
,
то маємо горизонтальну асимптоту.
На рис. 3 наведено графік
функції
![]() ,
вертикальних асимптот
,
вертикальних асимптот
![]() ,
,
![]() та нахиленої асимптоти
та нахиленої асимптоти
![]() .
.
2.6. Явно і неявно задані функції
Функція називається
заданою явною,
якщо вона задана формулою, в якій права
частина не містить залежної змінної,
наприклад, функція
![]() .
.
Функція називається
заданою неявною,
якщо вона задана рівнянням
![]() ,
не розв’язаним відносно залежної
змінної, наприклад, функція задана
рівнянням
,
не розв’язаним відносно залежної
змінної, наприклад, функція задана
рівнянням
![]() .
(Зауважимо, що останнє рівняння задає
дві функції,
.
(Зауважимо, що останнє рівняння задає
дві функції,
![]() для
для
![]() ,
і
,
і
![]() для
для
![]() ).
).
2.7. Параметрично задані функції
Якщо функціональна залежність між змінними х і у виражена через третю змінну, наприклад, t, що називається параметром, тобто
![]()
![]() ,
,
то кажуть, що функція у від змінної х задана параметрично.
Наприклад,
параметрично задана функція
![]()
![]() визначає рівняння кола з радіусом R.
Справді, якщо ліву і праву частину
кожного рівняння піднесемо до квадрату
і додамо, то, враховуючи, що
визначає рівняння кола з радіусом R.
Справді, якщо ліву і праву частину
кожного рівняння піднесемо до квадрату
і додамо, то, враховуючи, що
![]() ,
дістанемо відоме рівняння кола із
центром у початку координат
,
дістанемо відоме рівняння кола із
центром у початку координат
![]() .
.
2.8. Обернені функції
Нехай
є
функція від незалежної змінної х,
визначена на множині Х
із множиною значень Y.
Поставимо у відповідність кожному y
Y єдине
значення х
X, для якого
![]() .
Тоді одержана функція
.
Тоді одержана функція
![]() визначена на множині Y
з областю значень Х,
називається оберненою.
Наприклад, для функції y=ax
оберненою
буде функція y=logax.
визначена на множині Y
з областю значень Х,
називається оберненою.
Наприклад, для функції y=ax
оберненою
буде функція y=logax.
Можна показати, що для будь-якої строго монотонної функції y=f(x) існує обернена функція.
Щоб знайти функцію
обернену до заданої функції
,
достатньо розв’язати рівняння
відносно змінної x (якщо це можливо).
Оскільки кожна точка (x, y) кривої
є одночасно точкою кривої
то графіки взаємно обернених функцій
і
![]() збігаються.
Якщо ж додатково вимагається, щоб, як
звичайно, незалежна змінна позначалась
через х, а залежна – через y, то
замість функції
матимемо функцію
збігаються.
Якщо ж додатково вимагається, щоб, як
звичайно, незалежна змінна позначалась
через х, а залежна – через y, то
замість функції
матимемо функцію
![]() .
З цього випливає, що графіки взаємно
обернених функцій симетричні відносно
бісектриси першого і третього
координатних кутів, тобто прямої
.
.
З цього випливає, що графіки взаємно
обернених функцій симетричні відносно
бісектриси першого і третього
координатних кутів, тобто прямої
.
Нехай, наприклад,
потрібно знайти обернену функцію до
заданої функції
![]() .
Для цього розв’яжемо рівняння
.
Для цього розв’яжемо рівняння
![]() відносно змінної х:
відносно змінної х:
![]() і замінимо х на у і, навпаки, у
на х. Таким чином, обернена функція
до заданої буде мати вигляд
і замінимо х на у і, навпаки, у
на х. Таким чином, обернена функція
до заданої буде мати вигляд
![]() .
.
2.9. Складна функція
Нехай
функція
![]() є функція від незалежної змінної u,
визначена на множині
є функція від незалежної змінної u,
визначена на множині
![]() з областю значень
з областю значень
![]() ,
а змінна
,
а змінна
![]() у свою чергу є функцією
у свою чергу є функцією
![]() від змінної
від змінної
![]() ,
визначеної на множині
,
визначеної на множині
![]() з областю значень
.
Тоді задана на множині
функція
з областю значень
.
Тоді задана на множині
функція
![]() називається складною функцією або
функцією від функції.
називається складною функцією або
функцією від функції.
Наприклад,
![]() – складна функція, оскільки її можна
подати у вигляді
– складна функція, оскільки її можна
подати у вигляді
![]() ,
,
![]() .
.
