Метод секущих
Далеко не всегда бывает удобно находить аналитическое выражение для производной функции, в таком случае можно использовать метод секущих.
Для начала итерационного процесса необходимо задать два начальных приближения х0 и х1.
Если
х0 и x1
расположены достаточно близко друг к
другу, то производную
можно заменить ее приближенным значением
в виде отношения приращения функции
равного
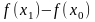к отношению приращения аргумента равного
(x1 – x0):
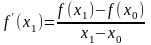(4)
Таким образом, формула метода секущих может быть получена из формулы Ньютона (2) заменой производной выражением (4) и записана в виде:
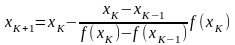(5)
Однако
следует помнить, что при этом нет
необходимости, чтобы значения функции
и
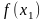обязательно имели разный знак, как в
методе половинного деления.
Процесс нахождения корня при использовании метода секущих можно считать законченным, когда выполняется следующее условие:
(6)
Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако не требует вычислений производной левой части уравнения.
Таким образом, для реализации метода секущих необходимо:
Задать в явном виде уравнение , корни которого необходимо определить.
Определить начальные приближения х0 и х1, обеспечивающие быструю сходимость метода.
Задать точность нахождения корня уравнения .
Реализовать в программе итерационную процедуру, реализующую формулу (5).
Результатом проведения лабораторной работы является программа, реализующая один из описанных методов с решением контрольного примера согласно, полученного индивидуального задания.
Метод простых итераций
Пусть дана функция
.
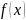Выразим х. В итоге у нас получится
выражение
.
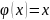Выберем начальное приближение
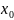и вычислим
.
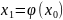Далее следует проделать эту операцию
до тех пор, пока
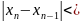ε.
В итоге
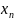будет являться корнем уравнения с
точностью до ε.
Таким образом, для реализации метода простых итераций необходимо:
Задать в явном виде уравнение
,
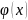наиболее приемлемо выразив х.Определить начальные приближения х0, обеспечивающие быструю сходимость метода.
Задать точность нахождения корня уравнения .
Реализовать в программе итерационную процедуру, реализующую вышеописанную формулу.
Нахождение количества и окрестностей корней на заданном отрезке.
Может получиться так, что корней у уравнения несколько и зависимость того, какой корень найдется, будет зависеть от заданного приближения. Чтобы найти количество корней на заданном отрезке, можно применить следующий метод:
Будем
просматривать значения функции через
заданный шаг. Если на i-ом
и на (i+1)-ом шаге функция
имеет разные знаки, она пересекает ось
Ох, соответственно имеет корень в
окрестности от
до
.
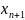При таком подходе может случиться так,
что график функции касается абсциссы,
но не пересекает её, для нахождения
такого корня потребуются аналитические
методы. Может случиться так, что на i-ом
шаге функция примет нулевое значение,
в таком случае корень будет найден
точно. После того, как найдены окрестности
корней, можно задать приближение,
входящее в окрестность данной функции
и вычислить корень более точно.
Описание алгоритма решения задачи
Для
вычисления значения функции введены
две подпрограммы, первая вычисляет
значение исходной функции
,
вторая реализована для метода простых
итераций, где был выражен х с коэффициентом
.
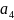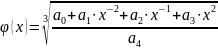
Причина, по которой была выражена именно
эта переменная заключается в следующем:
Х с отрицательной степенью не приемлет
нулевого значения. Х в квадрате не
приемлет отрицательные значения.
Единственное требование к значениям
коэффициентов, чтобы
.
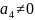Так же была введена функция подсчета
кубического корня, так как функция pow()
из пакета math.h
не работает с отрицательными значениями.
Интерфейс реализован с помощью циклов do while.
Сначала программа запрашивает значения коэффициентов и записывает их в массив
Далее пользователю предоставляется следующий выбор: Использовать метод простых итераций, метод секущих или посчитать количество корней функции. В результате выбора действия в символьную переменную записывается значение и если оно отличается от вышеуказанных, программа повторяет запрос вновь.
В методе секущих программа запрашивает точность решения и начальное приближение. Далее добавляет в файл исходный вид уравнения и введенные значения. После этого выполняет действия, описанные в теоретической части. Так же, во избежание проблем с нулевым значением и
,
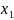программа производит проверку и в
случае нулевого значения переменной
прибавляет к ней ε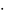
0.1.
Такой способ часто используется в
математическом анализе для вычисления
значения, близкого к нулю. В основном
цикле программа производит действия,
описанные выше. Для удобства сравнения
методов в файл, помимо найденного корня
записывается количество итераций, а
на экран каждый раз выводится точка,
что помогает визуально оценить скорость
решения уравнения.При выборе метода простых итераций программа запрашивает точность и начальное приближение, далее добавляет в файл исходный вид уравнения и введенные значения. Как и в методе секущих, программа отодвигается от нулевого значения на ε 0.1. В основном цикле вычисляются новые х по формуле
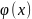до тех пор, пока разница между ними не
сократится до ε. Так же программа
помогает визуально оценить быстродействие
метода.Для поиска корней необходимо запросить шаг и интервалы. Далее стартует цикл с действительной переменной в качестве счетчика. Каждый раз её значение увеличивается на заданный шаг. В теле цикла программа проверяет значение
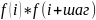и в случае отрицательного значения
выводит окрестность i и
(i+шаг) на экран. В случае
нулевого значения программа выдает
точный корень i. В целом
данный метод напоминает метод половинного
деления.
В конце пользователю предоставляется выбор либо выйти из программы, либо начать заново. Это было осуществлено с помощью цикла do while, где в случае неравенства символьной переменной символу q цикл продолжается.
Руководство программиста
Программный код приложения разрабатывался на языке СИ.
В программе использованы следующие пользовательские функции:
float cbrt (действительная переменная)
Вычисляет
модуль входной переменной в степени
0.33333333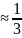
,
в случае отрицательного значения оной
меняет знак вычисления на противоположный.
float f (действительная переменная)
Вычисляет значение .
float fi(действительная переменная)
Вычисляет значение
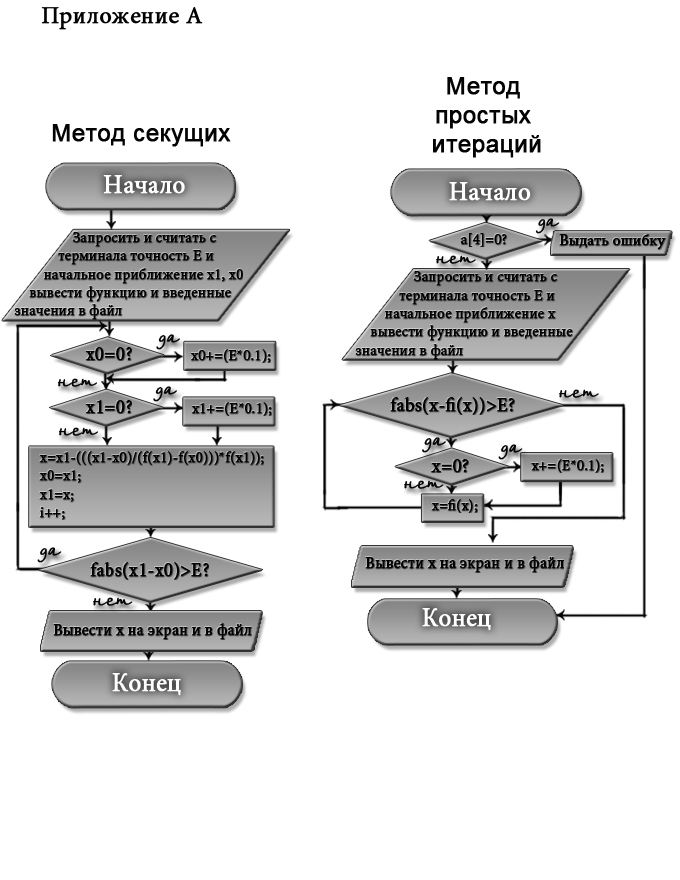
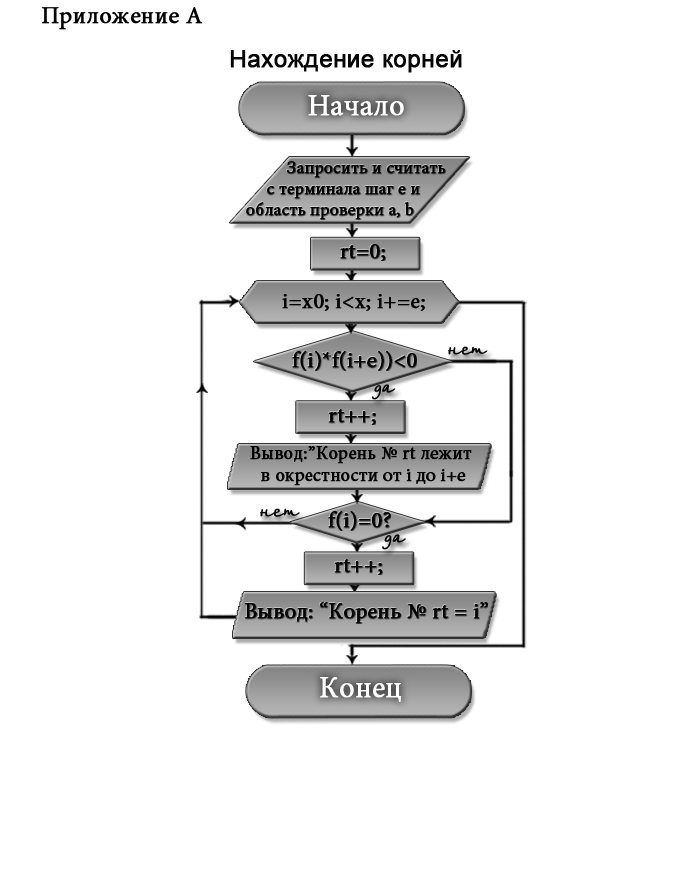
Основные моменты алгоритмов приведены на блок-схеме в приложении А.
Листинг программы приведен в приложении В.
Пример входного и выходного файла в приложении С.
Руководство пользователя
После
запуска программа запросит пять
коэффициентов
по указанной формуле. Если предполагается
использовать метод простых итераций,
коэффициент
,
иначе программа выдаст ошибку. Далее
пользователю будет предоставлен выбор
метода, либо программа может посчитать
корни на заданном интервале. Символы
можно вводить без учета регистра. В
методе секущих используются два значения
начальных приближений и оттого, насколько
они близки друг к другу, зависит скорость
работы программы. Также повышенная
точность требует большее количество
времени. Результаты работы программы
можно увидеть в файле OutputFunction.txt.
Так же на экране точками будет показано
количество действий. При поиске корней
задается интервал и шаг. Далее программа
выведет на экран либо окрестности, либо
сами корни уравнения. После этого,
используя в качестве начального
приближения окрестность корня, можно
вычислить его более точно. После
проделанной работы вычисление можно
повторить вновь, либо выйти, введя символ
q.
Сравнение методов по эффективности
Для Сравнения методов был разработан следующий программный код:
#include <stdio.h>
#include <math.h>
float a[5];
float cbrt(float a)
{
float b;
b=pow(fabs(a),0.3333333);
if (a<0) b=-b;
return b;
}
float f(float x)
{
float y=a[0]+a[1]*pow(x,-2)+a[2]*pow(x,-1)+a[3]*pow(x,2)+a[4]*pow(x,3);
return y;
}
float fi(float x)
{
float y=-cbrt((a[0]+a[1]*pow(x,-2)+a[2]*pow(x,-1)+a[3]*pow(x,2))/a[4]);
return y;
}
void main()
{
float E,x1c,x0c,x0,x1,x,xc;
FILE *P;
P=fopen("OutputFunctionM.txt","w");
printf("Input values for function F(x)=a0+a1*x^(-2)+a2*x^(-1)+a3*x^2+a4*x^3\n");
for(int i=0;i<5;i++)
scanf("%f", &a[i]);
printf("Input closeness (x0,x1)\n");
scanf("%f", &x0c);
fprintf(P,"\n F(x)=%0.2f+%0.2f*x^(-2)+%0.2f*x^(-1)+%0.2f*x^2+%0.2f*x^3 \n Slice method with closeness x0=%f, x1=%f;\n",a[0],a[1],a[2],a[3],a[4],x0c,x0c-0.1);
for(E=1;E>0.00001;E/=2){
x1=x0c+0.1;
x0=x0c;
int i=0;
do
{
if (x1==0) x1+=(E*0.1);
if (x0==0) x0+=(E*0.1);
x=x1-(((x1-x0)/(f(x1)-f(x0)))*f(x1));
x0=x1;
x1=x;
i++;
}
while((fabs(x1-x0)>E));
fprintf(P,"E=%f x=%f, i=%d\n",E,x,i);
}
fprintf(P,"\n F(x)=%0.2f+%0.2f*x^(-2)+%0.2f*x^(-1)+%0.2f*x^2+%0.2f*x^3 \nSimple iteration method closeness x0=%f\n",a[0],a[1],a[2],a[3],a[4],x0c);
for(E=1;E>0.00001;E/=2){
int i=0;
x=x0c;
if (x==0) x+=(E*0.1);
while(fabs(x-fi(x))>E)
{
x=fi(x);
i++;
if (x==0) x+=(E*0.1);
}
fprintf(P,"E=%f x=%f, i=%d\n",E,x,i);
}
}
Программа запрашивает коэффициенты, приближение и увеличивает точность в два раза. Результаты выводит в файл вместе с количеством итераций. Выберем два набора произвольных коэффициентов, например (1,2,3,4,5) и (-1,3,10,0,-2). Далее взяв три различных начальных приближения, и для каждого составим таблицу в MS Excel(так как для метода секущих требуется два начальных приближения, а для итераций одно, возьмем близкие друг к другу значения, из аналитических соображений понятно, что чем дальше значения друг от друга, тем менее эффективно будет работать метод):
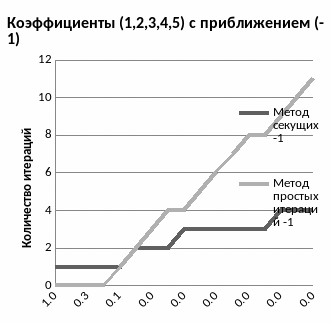
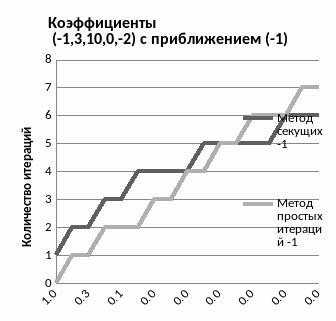
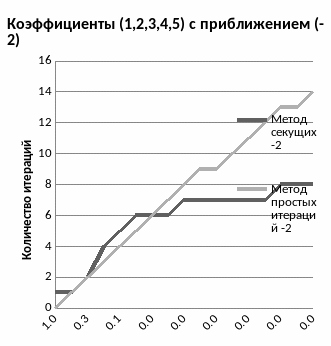
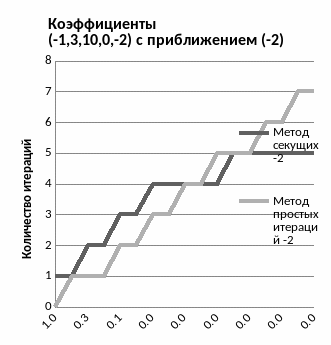
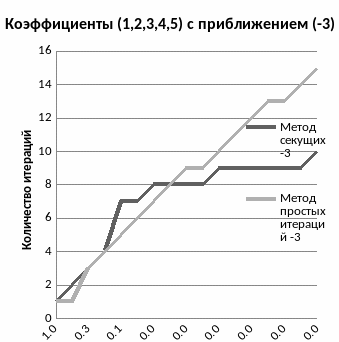
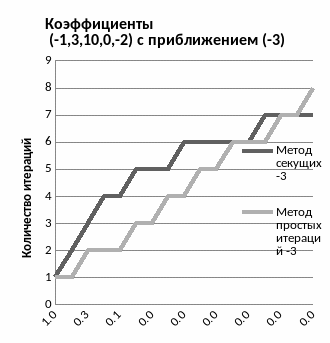
Как видно из графиков, метод секущих выигрывает по скорости перед методом итераций. С увеличением точности количество действий в методе секущих увеличивается не линейно, как в методе итераций, а, начиная с какой-то точки, замедляет свой рост. Так же оба метода зависят от начального приближения и, чем ближе оное находится к корню, тем быстрее будет выполнен подсчет.
Приложение
В
#include <stdio.h>
#include <math.h>
float a[5];
float cbrt(float a)
{
float b;
b=pow(fabs(a),0.3333333);
if (a<0) b=-b;
return b;
}
float f(float x)
{
float y=a[0]+a[1]*pow(x,-2)+a[2]*pow(x,-1)+a[3]*pow(x,2)+a[4]*pow(x,3);
return y;
}
float fi(float x)
{
float y=-cbrt((a[0]+a[1]*pow(x,-2)+a[2]*pow(x,-1)+a[3]*pow(x,2))/a[4]);
return y;
}
void main()
{
float E,x0,x1,x;
char w;
FILE *P;
P=fopen("OutputFunction.txt","w");
do
{
printf("Input values for function F(x)=a0+a1*x^(-2)+a2*x^(-1)+a3*x^2+a4*x^3\n");
for(int i=0;i<5;i++)
scanf("%f", &a[i]);
do
{
printf("Choose way of root calculation: simple iteration method(I), silce method(S) or search of value of roots(R)\n");
scanf(" %c",&w);
}
while(w!='i' && w!='s' && w!='I' && w!='S' && w!='R' && w!='r');
if(w=='s' || w=='S')
{
printf("Input accuracy (E)\n");
scanf("%f", &E);
printf("Input closeness (x0,x1)\n");
scanf("%f %f", &x0, &x1);
int i=0;
fprintf(P,"F(x)=%0.2f+%0.2f*x^(-2)+%0.2f*x^(-1)+%0.2f*x^2+%0.2f*x^3 \nSilce method was used with accuracy E=%f; closeness x0=%f, x1=%f;",a[0],a[1],a[2],a[3],a[4],E,x0,x1);
do
{
if (x1==0) x1+=(E*0.1);
if (x0==0) x0+=(E*0.1);
x=x1-(((x1-x0)/(f(x1)-f(x0)))*f(x1));
x0=x1;
x1=x;
printf(".");
i++;
}
while((fabs(x1-x0)>E));
printf(" \n %f \n", x);
fprintf(P," Root of function is %f \n number of iterations is %d \n \n",x,i);
}
if(w=='i' || w=='I')
{
if (a[4]!=0)
{
int i=0;
printf("Input accuracy (E)\n");
scanf("%f", &E);
printf("Input closeness (x0)\n");
scanf("%f", &x);
fprintf(P,"F(x)=%0.2f+%0.2f*x^(-2)+%0.2f*x^(-1)+%0.2f*x^2+%0.2f*x^3 \nSimple iteration method was used with accuracy E=%f; closeness x0=%f",a[0],a[1],a[2],a[3],a[4],E,x);
if (x==0) x+=(E*0.1);
while(fabs(x-fi(x))>E)
{
x=fi(x);
printf(".");
i++;
if (x==0) x+=(E*0.1);
}
printf("\n %f \n", x);
fprintf(P," Root of function is %f \n number of iterations is %d \n \n",x,i);
}
else
printf("a4 cannot be equal 0 with this method");
}
if(w=='r' || w=='R')
{
printf("Enter step(e) and area of roots(a,b) \n");
scanf("%f %f %f",&E,&x0,&x1);
int rt=1;
for(float i=x0;i<x1;i+=E)
{
if((f(i)*f(i+E))<0) printf("Root # %d is inside area x=(%f,%f)\n",rt++,i,(i+E));
if (f(i)==0) printf("Root # %d is %f",rt,i);
}
}
printf("Do you want to quit this brilliant program? (Q)");
scanf(" %c",&w);
}
while(w!='Q' && w!='q');
}
Приложение С
Выходной файл OutputFunction.txt:
F(x)=1.00+2.00*x^(-2)+3.00*x^(-1)+4.00*x^2+5.00*x^3
Slice method was used with accuracy E=0.010000; closeness x0=-1.000000, x1=1.000000; Root of function is -0.859077
number of iterations is 3
F(x)=1.00+2.00*x^(-2)+3.00*x^(-1)+4.00*x^2+5.00*x^3
Simple iteration method was used with accuracy E=0.010000; closeness x0=-1.000000 Root of function is -0.873077
number of iterations is 3