- •Неопределенные интегралы
- •Определенные интегралы
- •Задача 1 Интегрирование по частям
- •Задача 2 Интегрирование по частям
- •Задача 3 Интегрирование подведением под знак дифференциала
- •Задача 4 Интегрирование подведением под знак дифференциала
- •Задача 5 Интегрирование рациональных функций с простыми вещественными корнями знаменателя
- •Задача 6 Интегрирование рациональных функций с кратными вещественными корнями знаменателя
- •Задача 7 Интегрирование рациональных дробей с простыми комплексными корнями знаменателя
- •Задача 8 Интегрирование выражений
- •Задача 9 Интегрирование выражений
- •Задача 10 Интегрирование выражений
- •Задача 13 Интегрирование дифференциального бинома
- •Задача 14 Вычисление площадей в декартовых координатах
- •Задача 15 Вычисление площадей в случае, когда уравнение линии задано параметрически
- •Задача 16 Вычисление площадей в полярных координатах
- •Задача 17 Вычисление длин дуг
- •Задача 18 Вычисление длин дуг
- •Задача 19 Вычисление длин дуг
- •Задача 20 Вычисление объемов по площадям поперечных сечений
- •Задача 21 Вычисление объемов тел вращения
Задача 14 Вычисление площадей в декартовых координатах
Постановка задачи. Вычислить
площадь области, ограниченной графиками
функций
![]() и
и
![]() (
(![]() или
или ![]() для всех точек области) и, возможно,
прямыми
для всех точек области) и, возможно,
прямыми ![]() и
и
![]() .
.
План решения. Если область
![]() задана
системой неравенств
задана
системой неравенств
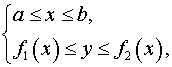
то площадь области находится по формуле
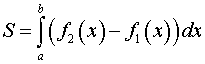 .
.
Если неравенства, определяющие область
,
неизвестны, т.е. неизвестны ![]() и
и
![]() и
неизвестно, какая из функций
и
неизвестно, какая из функций
![]() и
и
![]() больше
на
больше
на
![]() ,
то выполняем следующие операции.
,
то выполняем следующие операции.
1. Находим и как абсциссы точек пересечения графиков функций и , т.е. решаем уравнение
![]() .
.
2. Исследуем знак разности
![]() на
на
![]() .
Для этого достаточно вычислить значение
в
какой-нибудь точке из
.
Если оно положительно, то
и
.
Для этого достаточно вычислить значение
в
какой-нибудь точке из
.
Если оно положительно, то
и
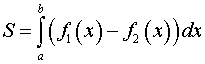 ;
;
если оно отрицательно, то и
.
Замечание. Иногда бывает полезным построить график области , ограниченной функциями и .
Задача 14. Вычислить площади фигур, ограниченных графиками функций.
![]()
Вычисляем площадь:

Задача 15 Вычисление площадей в случае, когда уравнение линии задано параметрически
Постановка задачи. Вычислить
площадь области, ограниченной графиком
функции, заданной параметрически
![]() и,
возможно, прямыми
и,
возможно, прямыми
![]() или
или
![]() .
.
План решения.
Формула вычисления площади области в случае, когда уравнение линии задано параметрически:
 .
(1)
.
(1)
1. Вычисляем
![]() .
.
2. По формуле (1) находим искомую площадь.
Замечание. Иногда бывает полезным построить график области, ограниченной графиком функции, заданной параметрически .
Задача 15. Вычислить площади фигур, ограниченных линиями, заданными уравнениями.

Строим график функции.

Необходимо найти площадь области
![]() .
.
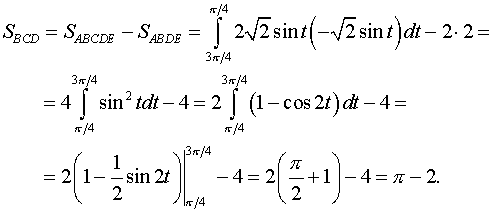
Пределы интегрирования найдены из решения неравенства
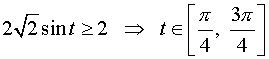 .
.
Задача 16 Вычисление площадей в полярных координатах
Постановка задачи. Вычислить
площадь области, ограниченной графиками
функций
![]() и
и
![]() .
.
План решения.
Формула вычисления площади области в полярных координатах:
 .
.
Если
![]() ,
то эта формула принимает вид:
,
то эта формула принимает вид:
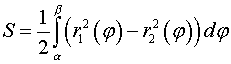 .
.
Замечание. Иногда бывает полезным построить график области, ограниченной графиками функций и .
Задача 16. Вычислить площади фигур, ограниченных линиями, заданными в полярных координатах.
![]() .
.
Строим график:
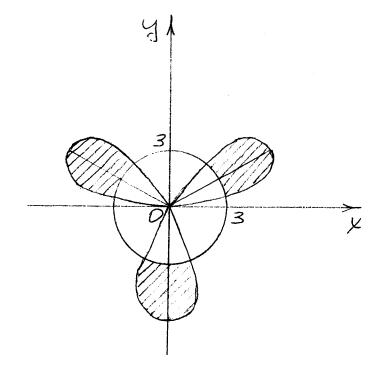
Пользуясь симметричностью фигуры, вычисляем:

Задача 17 Вычисление длин дуг
Постановка задачи. Вычислить длину дуги кривой, заданной уравнением
и ограниченной точками с абсциссами
и
![]() .
.
План решения.
Длина
![]() кусочно-гладкой
кривой
,
ограниченной точками с абсциссами
и
,
равна
кусочно-гладкой
кривой
,
ограниченной точками с абсциссами
и
,
равна
 .
(1)
.
(1)
1. Находим
![]() .
.
2. Вычисляем дифференциал дуги
![]() .
.
3. Находим длину дуги, воспользовавшись формулой (1).
Задача 17. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
![]() .
.
Находим производную.
![]() .
.
Тогда
 .
.
Задача 18 Вычисление длин дуг
Постановка задачи. Вычислить длину дуги кривой, заданной параметрически
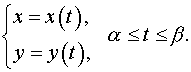
План решения.
Если кривая задана уравнениями в параметрической форме
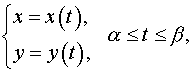
где – кусочно-гладкие функции, то длина дуги кривой вычисляется по формуле
 ,
(1)
,
(1)
где
![]() и
и
![]() –
значения параметра, соответствующие
граничным точкам дуги.
–
значения параметра, соответствующие
граничным точкам дуги.
1. Находим
![]() и
и
![]() .
.
2. Вычисляем дифференциал дуги
![]() .
.
3. По формуле (1) находим длину дуги.
Задача 18. Вычислить длины дуг кривых, заданных параметрическими уравнениями.

Находим:

Тогда