Form3 – о программе

Private Sub Command1_Click()

Unload Form3

End Sub

Form4 – Исследование

Private Sub Command1_Click()

Dim s As Double

Dim h As Double

Dim n As Long

Dim n1 As Long

a = 0

b = 1.7

Picture1.Scale (-10, 0.2)-(215, -0.01)

Picture1.Line (-10, 0)-(215, 0)

Picture1.Line (0, 0.2)-(0, -0.01)

Label1.Visible = True

Label2.Visible = True

Label3.Visible = True

Label4.Visible = True

Line1.Visible = True

Line2.Visible = True

j = 0

For n = 10 To 200 Step 10

h = (b - a) / n

s = 0

X1 = a

For i = 1 To n - 1

X1 = X1 + h

s = s + Fn(X1)

Next

F1 = h * (Fn(a) + Fn(b) + 2 * s) / 2

h = (b - a) / n

s = 0

x = b

For i = 1 To n - 1

F = Fn(x)

s = s + F

x = x - h

Next i

F2 = s * h

F3 = ff(b)-ff(a)

Et(j) = Abs(F1 - F3)

Ep(j) = Abs(F2 - F3)

j = j + 1

Next n

n = 10

For i = 0 To j

Picture1.Line (n, Et(i))-(n + 10, Et(i + 1)), vbRed

Picture1.Line (n, Ep(i))-(n + 10, Ep(i + 1)), vbBlue

Picture1.Line (n, 0)-(n, -0.001)

Picture1.Print n

n = n + 10

If n = 200 Then Exit For

Next

For i = 0 To 0.19 Step 0.01

Picture1.Line (0, i)-(1, i)

Picture1.Print i

Next

End Sub

Private Sub Command2_Click()

Label1.Visible = False

Label2.Visible = False

Label3.Visible = False

Label4.Visible = False

Line1.Visible = False

Line2.Visible = False

Picture1.Cls

End Sub

Private Sub Command3_Click()

Form4.Hide

Form1.Show

End Sub

Private Sub Command4_Click()

End

End Sub

Модуль

Public Ep(100)

Public Et(100) As Double

Public Function Fn(x)

Fn = x * Atn(x)

End Function

Public Function ff(t)

ff = (-0.5 * t + 0.5) * Exp(t) * Cos(t) + 0.5 * t * Exp(t) * Sin(t)

End Function

Руководство пользователю

Пользователь сначала должен ввести с клавиатуры данные (a, b, n). После этого, он вычисляет интеграл двумя методами, а точное решение находит по формуле Ньютона-Лейбница. Выполнив основные шаги можно двигаться дальше, т.е. переходить в окно визуализации метода, а потом переходить к построению графиков зависимости погрешностей методов. Некоторые результаты пользователь может сохранить в текстовом файле.

Заключение

После того, как мы вычислили интеграл 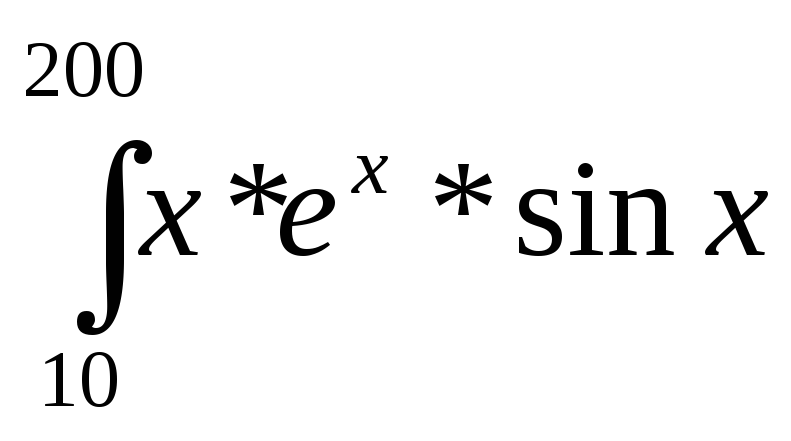dxдвумя методами

(прямоугольников и трапеций), сравнили полученные результаты с точным решением, рассчитанным по формуле Ньютона – Лейбница, построили графики зависимости погрешностей методов от числа разбиений, мы увидели, что для функции y=x*e метод трапеций точнее.

Список используемой литературы

1. Лукин С.Н. Visual Basic. Самоучитель для начинающих. - М.:”Диалог - МИФИ”, 2003.

2. Волченков Н.Г. Программирование на Visual Basic 6: В 3-х частях. Часть 3.-М.: ИНФРА-М, 2002.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т 1.”Наука” - М,1978.

4. Лекции по информатике.

18