2. Электрическая проводимость растворов электролитов

Электролиты – это вещества, диссоциирующие в среде растворителя на ионы. Под влиянием приложенного электрического поля образующиеся ионы движутся направленно и переносят электрический ток. Следовательно, электролиты – ионные проводники, в отличие от электронных проводников – металлов. Электролиты в зависимости от степени диссоциации можно разделить на сильные и слабые. Первые – это те, у которых существующие валентные связи преимущественно электростатические (кристаллы солей), а вторые – это вещества с преимущественно ковалентными связями (органические и некоторые минеральные кислоты и основания). Степень диссоциации электролита в растворе зависит от его природы, концентрации и от природы растворителя. Основным свойством растворителя, влияющим на степень диссоциации вещества, является его диэлектрическая проницаемость Вещества, которые в растворителях с большой диэлектрической проницаемостью диссоциированы практически полностью, в растворах с низкой диэлектрической проницаемостью почти не диссоциируют.

Независимо от степени диссоциации электролита раствор всегда остается электронейтральным, т.е. число положительных и отрицательных зарядов в растворе равны. Если электролит K_ν+A_ν– диссоциирует на ν₊ катионов с зарядом z⁺ и ν_– анионов с зарядом z^–

K_ν+A_ν– = ν₊K^z+ + ν_– A^z–, (2.1)

то в силу электронейтральности раствора ν₊z⁺ = ν_–z^–. Сказанное справедливо и при замене чисел ионов на их концентрации с₊z⁺ = с_–z .

При переносе электрического тока в проводниках любого типа возникает сопротивление, численное значение которого зависит от природы проводника, особенностей его строения, природы переносчика электрического тока.

Сопротивление проводника любого вида R, Ом, пропорционально его длине l, м, и обратно пропорционально сечению S, м²:

R (2.1)

где ρ – удельное сопротивление, Ом ∙ м, равное сопротивлению R при единичных длине l и сечении S проводника.

Электрическая проводимость Ω, (См = Ом ^–1 ) – величина, обратная сопротивлению:

. (2.2)

Величина æ, обратная удельному сопротивлению ρ, называется удельной электрической проводимостью и представляет собой электропроводность единичного объема раствора (1 м³), помещенного между параллельными плоскостями единичной площади (1 м²), находящимися на расстоянии друг от друга, равном единице (1 м). Удельная проводимость измеряется в См ∙ м^–1.

Согласно закону Ома, ток, проходящий через проводник, можно выразить как

. (2.3)

Тогда плотность тока i, А/м² , проходящего через проводник, может быть выражена как

, (2.4)

где U/l = Х – напряженность электрического поля, В/м.

В отсутствии электрического поля ионы в растворе находятся в состоянии хаотического теплового движения, совершая хаотичные перемещения в различных направлениях. При возникновении градиента потенциала ионы приобретают направленное движение. Скорость их перемещения υ_i, м/с, пропорциональна напряженности электрического поля (катионы под действием электрического поля перемещаются к катоду, анионы – к аноду):

υ_i = u_iХ (2.5)

Коэффициент пропорциональности u_i называют электрической подвижностью иона, она равна скорости движения иона при единичной напряженности электрического поля (м² ∙ В^–1 ∙ с^-1).

Плотность тока, переносимого катионами и анионами, пропорциональна их заряду z, концентрации с (кмоль/м³) и скорости направленного движения υ_i (м/с):

i₊ = z₊с₊υ₊F = z₊с₊u₊ХF, (2.6)

i_– = z_–с_–υ_–F = z_–с_–u_–ХF, (2.7)

где F – число Фарадея.

Суммарная плотность тока ионов обоих знаков

i = i₊ + i_– = z_iс_iХF(u₊ + u_–), (2.8)

поскольку с₊z₊ = с_–z_–.= с_iz_i

Сравнивая полученное уравнение (2.8) с уравнением (2.4), найдем удельную электрическую проводимость раствора:

æ = z_iс_iF(u₊ + u_–). (2.9)

Сильные электролиты диссоциируют в растворах полностью (если концентрация не слишком велика), поэтому концентрацию ионов любого знака можно выразить через концентрацию электролита в растворе с, кмоль/м³:

с_i = ν_iс, (2.10)

где ν_i – число ионов данного знака образующихся при диссоциации электролита.

Следовательно,

æ = z_iν_iсF(u₊ + u_–) = zсF(u₊ + u_–), (2.11)

где z_iν_i = z – число моль экв в единице объема, моль экв/м³.

Из уравнения (2.11) следует, что удельная электрическая проводимость сильных электролитов зависит от концентрации электролита и подвижности ионов.

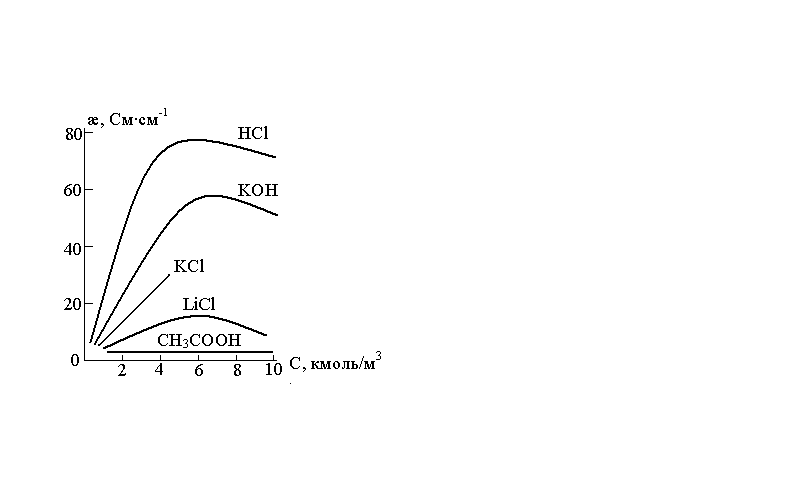
С увеличением концентрации вследствие электростатического взаимодействия между ионами снижается их подвижность. Влияние этих факторов может привести к появлению максимума на изотерме удельной электрической проводимости (рис. 4). При малых концентрациях расстояние между ионами велико, электростатическое взаимодействие незначительно, удельная электрическая проводимость растет с ростом концентрации вследствие появления большего количества заряженных частиц. По мере увеличения концентрации за счет проявления сил межионного взаимодействия подвижность ионов снижается в большей степени, чем растет их концентрация

Рис. 4. Концентрационная зависимость удельной электрической провод сильных и слабых электролитов

При растворении слабых электролитов даже в полярных растворителях, имеющих высокую диэлектрическую проницаемость, часть молекул не диссоциирует. Концентрация ионов в растворах слабых электролитов зависит от степени диссоциации α, представляющей собой отношение числа распавшихся на ионы молекул к общему числу растворенных молекул. Заменив концентрацию ионов с_i в уравнении (2.11) на с_i = αν_iс, получим выражение удельной электрической проводимости слабого электролита:

æ = z_iν_iсαF(u₊ + u_–) = zсαF(u₊ + u_–). (2.12)

Можно считать, что электростатическое взаимодействие между ионами в растворах слабых электролитов практически не проявляется, поскольку их концентрация невелика, а расстояния между ними значительны. Поэтому подвижности ионов в таких электролитах практически не зависят от концентрации раствора. Из уравнения (2.12) следует, что удельная электрическая проводимость растворов слабых электролитов должна зависеть от значения произведения αс. При низких концентрациях раствора это произведение увеличивается с ростом концентрации, и удельная электрическая проводимость повышается. Однако при больших концентрациях это произведение имеет тенденцию к уменьшению, вследствие чего удельная электрическая проводимость слабых электролитов после достижения максимального значения снижается.

Наряду с удельной проводимостью для количественной характеристики способности проводников II рода проводить электрический ток применяют понятие молярной и эквивалентной электрической проводимости.

Молярную электрическую проводимостью (λ_м) можно оценить как отношение удельной электрической проводимости к концентрации электролита:

, (2.13)

где с_м – молярность раствора, кмоль/м³.

Молярная электрическая проводимость равна проводимости раствора, помещенного между параллельными плоскостями, расположенными на расстоянии 1м друг от друга и имеющими площадь, достаточную для размещения 1 моль электролита, м². Молярную электрическую проводимость выражают в См ∙ м² ∙ моль^-1. Чаще пользуются эквивалентной электрической проводимостью:

, (2.14)

где с_экв – концентрация в кмоль экв/м³.

Эквивалентная электрическая проводимость измеряется в См ∙ м² ∙ моль экв^-1. Так как концентрации с_м и с_экв связаны уравнением

с_экв = с_мz (2.15)

где z – число моль экв в одном моль вещества, то

λ_м = λ_эквz (2.16)

При сочетании уравнений (2.12), (2.15) и (2.16) получим выражение молярной и эквивалентной электрических проводимостей сильных электролитов

λ_м = zF(u₊ + u_–), (2.17)

λ_э = F(u₊ + u_–) = Fu₊+ Fu_– = λ₊ + λ_– (2.18)

Произведения Fu₊ = λ₊ и Fu_– = λ_– называют эквивалентными электрическими проводимостями катиона и аниона или ионными подвижностями.

Эквивалентная электрическая проводимость иона, умноженная на его валентность, равна ионной электрической проводимости:

λ^´₊ = z⁺λ₊, λ^´_– = z^–λ _– (2.19)

С учетом соотношения (2.19) молярную электрическую проводимость можно выразить как сумму ионных электрических проводимостей:

λ_м = ν₊λ^´₊ + ν_–λ^´_–.. (2.20)

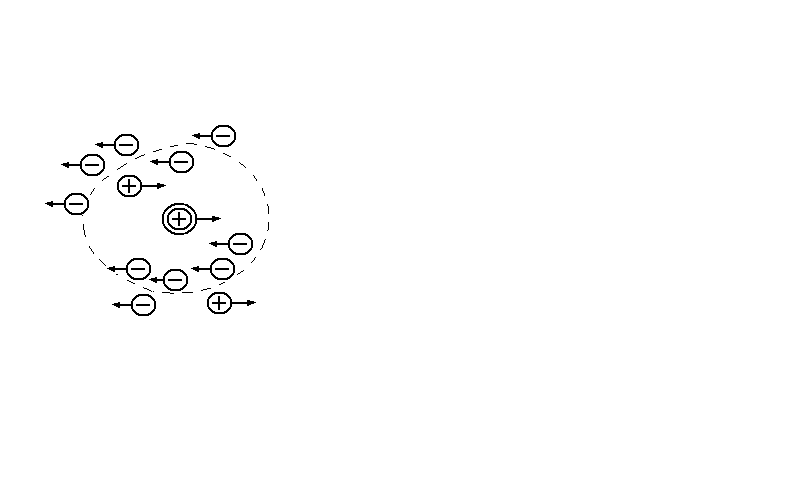
Рис.5. Движение центрального иона и ионной атмосферы в электрическом поле

Зависимость эквивалентной электрической проводимости водных растворов сильных электролитов от концентрации в основном определяется силами межионного взаимодействия, зависящими от расстояния между ионами. В растворе электролита сольватированные (гидратированные) ионы находятся в тепловом движении и расположение их более беспорядочно, чем в кристалле. Вследствие электростатических сил взаимодействия между ионами даже в разбавленных растворах распределение их не может быть случайным. Притяжение разноименно заряженных ионов и отталкивание одинаково заряженных должно приводить к тому, что в среднем вблизи каждого положительного иона возникнет избыток отрицательных ионов (и наоборот). Каждый ион окружен ионной атмосферой, заряд которой равен и противоположен по знаку заряду центрального иона (рис. 5). Наличие ионной атмосферы вызывает взаимное торможение ионов при их движении в электрическом поле. Движение ионной атмосферы в сторону противоположную движению иона вызывает электрофоретическое (или катафоретическое) торможение. Если бы двигался только центральный ион (любой ион может быть выбран в качестве центрального), сопротивление движению определялось бы трением между сольватной оболочкой движущегося иона и окружающей жидкостью (растворителем). В процессе перемещения ионов под действием электрического поля окружающая жидкость вовлекается в движение ионной атмосферой и создает встречный поток жидкости, который увеличивает силу трения, тормозящую движение иона.

При движении любого иона нарушается сферическая симметрия его ионной атмосферы. Рассеивание существующей и образование новой атмосферы вокруг движущегося иона происходит не мгновенно, для восстановления ее требуется некоторое время, так называемое время релаксации, которое в первом приближении можно оценить из соотношения τ_р = 10^–10/с. В результате при движении иона впереди него ионная атмосфера не успевает сформироваться, а позади не успевает полностью разрушиться, в связи с чем плотность противоположного заряда впереди движущегося иона несколько понижена, а позади – повышена. Некоторый избыток противоположных зарядов позади иона вызывает так называемое релаксационное торможение.

Чем выше концентрация раствора, тем значительнее эти эффекты, вызывающие уменьшение подвижности ионов, и, следовательно, эквивалентной электрической проводимости электролитов.

Теоретический расчет, выполненный Дебаем и Хюккелем на основании электростатической (кристаллоподобной) модели строения растворов электролитов, показывает, что в разбавленных растворах (с_экв << 0,01кмоль экв/м³) уменьшение электрической проводимости, вызываемое взаимным торможением ионов, пропорционально корню квадратному из концентрации. Зависимость λ_м и λ_экв от для таких растворов выражается прямой линией. Уравнение, описывающее эту зависимость, имеет вид:

λ_э = λ₀ – (А + Вλ₀) , (2.21)

где А и В – коэффициенты, зависящая от природы растворителя, его диэлектрической проницаемости, вязкости, природы электролита и температуры; λ₀ – эквивалентная проводимость при бесконечном разбавлении.

В бесконечно разбавленных растворах электролитов (с → 0) межионное взаимодействие практически отсутствует и эквивалентная электрическая проводимость стремится к предельному значению: λ_экв → λ₀. Уравнения (2.17) и (2.18) можно тогда записать так:

λ_э = λ₀ = λ₀,₊ + λ₀,_– , λ_{0, м} = ν₊λ^´_0,+ + ν_–λ^´_0,– . (2.22)

Это уравнение отражает закон Кольрауша о независимости движения ионов: в электрическом поле ионы переносят электрический ток независимо друг от друга.

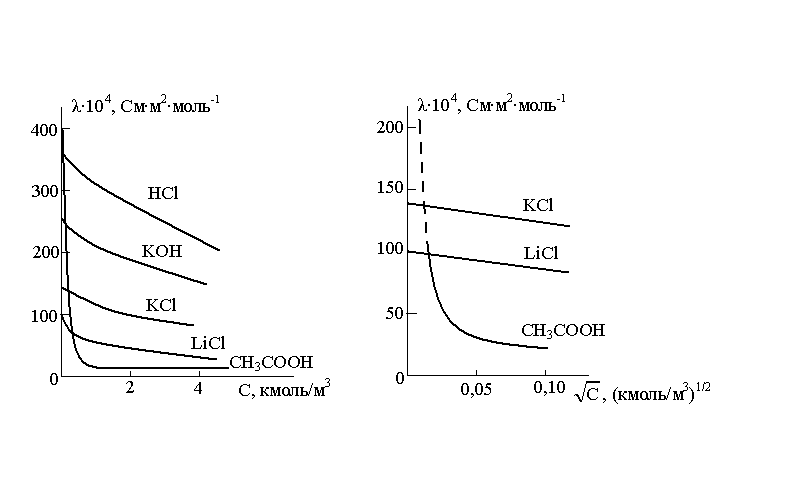
Несмотря на то, что λ₀ есть предельная эквивалентная электрическая проводимость при с → 0, ее нельзя приравнивать к электрической проводимости растворителя. Зависимость эквивалентной электрической проводимости электролитов от с и , показана на рис. 6. Сильные электролиты имеют высокую эквивалентную электрическую проводимость даже в концентрированных растворах. С ростом концентрации снижение эквивалентной проводимости объясняется уменьшением подвижности ионов. Отношение λ_экв к ее предельному значению λ₀ называют коэффициентом электрической проводимости f:

f_λ = λ_экв / λ₀ (2.23)

а б Рис. 6. Зависимость эквивалентной электрической проводимости от концентрации

В растворах слабых электролитов межионные взаимодействия слабы и ионы движутся независимо друг от друга при любой концентрации, т. е. в уравнении (2.17) можно заменить F(u₊ + u_–) = = F(u_о,+ + u_о,–) на λ₀ и zF(u₊ + u_–) на λ_{0, м}. Тогда выражение удельной электрической проводимости слабых электролитов примет вид

æ = zсαλ₀ = сαλ_{0, м} . (2.24)

Сопоставление этого уравнения с уравнениями (2.18) и (2.19) дает:

λ_м = αλ_0,м, λ_э = αλ₀ (2.25)

Следовательно, степень диссоциации слабого электролита может быть найдена из отношений

. (2.26)

Эквивалентная (и молярная) электрическая проводимости слабых электролитов, как и сильных, уменьшается с ростом концентрации, но причиной этого является уменьшение степени диссоциации. На рис. 6, а показано, что λ_экв для слабых электролитов даже в разбавленных растворах имеет низкое значение и резко возрастает по мере приближения к бесконечному разведению, достигая при с_экв → 0, предельного значения. Линейная зависимость λ _экв от отсутствует, но при малых концентрациях линейна зависимость λ _экв от .

Предельную эквивалентную электрическую проводимость сильных электролитов можно найти посредством экстраполяции опытных данных λ_экв = f ( ) к с_экв → 0 (рис. 6, б). К слабым электролитам этот способ неприменим. В основе определения λ₀ слабого электролита лежит закон независимости подвижностей ионов, позволяющий суммировать эквивалентные электрические проводимости ионов, составляющих электролит. Этот способ определения λ₀ можно применять и к сильным электролитам.

Если табличные данные для ионов, составляющих электролит, отсутствуют, можно найти λ₀ слабого электролита посредством комбинации λ₀ сильных электролитов, определенных экстраполяцией. Так, например, для определения λ₀ уксусной кислоты находят в таблицах λ₀ СНзСООNа, НС1 и NаС1 и далее вычисляют:

λ₀, _{СНзСООН} = λ₀, _{СНзСООNа} + λ₀, _НС1 – λ₀, _NаС1

Предельные эквивалентные электрические проводимости ионов при 25° С заключены в интервале (35–80) ∙ 10^–4 См ∙ м² ∙ моль экв^-1, но электрические проводимости ионов Н⁺ и ОН^– значительно больше и равны 349,8 ∙ 10^–4 См ∙ м² ∙ моль экв^-1 и 198,3 ∙ 10^–4 См ∙ м² ∙ моль экв^-1 Большая подвижность этих ионов объясняется эстафетным механизмом переноса заряда.

С повышением температуры уменьшается вязкость и диэлектрическая проницаемость растворителя. Вследствие понижения вязкости уменьшается электрофоретическое торможение и электрическая проводимость увеличивается. Понижение диэлектрической проницаемости способствует уменьшению степени диссоциации слабых электролитов и увеличению релаксационного торможения сильных электролитов, следовательно, ведет к понижению электрической проводимости. Однако второе явление сказывается незначительно, если ограничиваться температурами около 25°С. В таких условиях λ с повышением температуры на один градус возрастает на 1,5–2%.