5.4. Порядок выполнения работы

Исходные данные для расчета представить в виде двух векторов x и y и графика с кусочно-линейной интерполяцией.

Решить задачу интерполяции, используя формулу Лагранжа. Воспользоваться программой для расчета значений интерполяционного полинома и рассчитать промежуточные значения в таблицах.

Определить промежуточные значения при помощи сплайн-интерполяции.

Построить графики интерполяции: кусочно-линейной, сплайном и обычным полиномом.

Составить таблицу промежуточных значений, полученных разными способами интерполяции. Сделать анализ полученных результатов.

5.5.Пример выполнения работы

. Рассмотрим выполнение лабораторной работы на примере первого задания из таблицы 5.1.Выполнение расчетов будем производить при помощи программы Маthcad. Исходные данные для расчета.

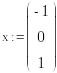
Воспользуемся графическими возможностями Маthcad для визуализации исходных данных.По оси х отложим дискретные значения x_i, а по оси y соответственно y_i.

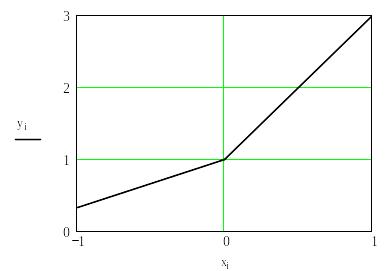
Рис.5.4. Кусочно-линейная графическая интерполяция исходных данных средствами Mathcad.

При построении графика для дискретных значений x_i и y_i Mathcad автоматически осуществляет их кусочно-линейную интерполяцию, результаты которой показаны на рис.5.4.

Сначала будем решать задачу интерполяции, используя формулу Лагранжа и подпрограмму для определения промежуточных точек, представленную на рис.5.3.

Подпрограмма позволяет получить все необходимые значения функции, в том числе и при промежуточных значениях аргумента.

Запишем имеющиеся данные при помощи двух пар векторов. Векторы z₁ и f₁ соответствуют исходным данным, а векторы z и f полному набору точек с учетом полученных промежуточных значений.

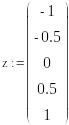
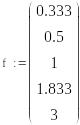
Представим записанные векторы в графическом виде с использованием автоматической кусочно-линейной интерполяции Маthcad.

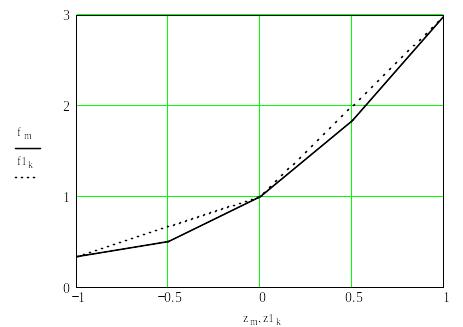
Рис.5.5.Кусочно-линейная графическая интерполяция данных: f1k - исходные, fm - дополненные расчетом по формуле Лагранжа.

На рис.5.5 заметно различие значений функции в промежуточных точках, полученных интерполяцией обычными полиномами и интерполяцией кусочно-линейными функциями.

Интерполяционный полином Лагранжа в трехточечной схеме деления промежутка интерполирования можно записать в виде (5.4)

После подстановки исходного вектора данных: x₀=-1, x₁=0, x₂=1 и y₀=0.333, y₁=1, y₂=3 интерполяционный полином примет следующий вид:

Используя символьные преобразования Mathcad, получим

(5.7)

Значения этого полинома при zx=-0.5 и zx=0.5

cоответствуют полученным ранее при помощи подпрограммы.

Интеполяционная кривая, полученная при помощи обычного полинома, показана на рис.5.6.

В Mathcad имеются операторы автоматической интерполяции дискретных данных: linterp и interp.

Оператор linterp(v_x,v_y,x) осуществляет кусочно-линейную интерполяцию векторов исходных данных v_x и v_y для точки x.

Применяя его для нашей задачи, получим

Непрерывная кривая

для кусочно-линейной интерполяции показана на рис.5.6.

Оператор inter(v_s,v_x,v_y,x) возвращает интерполированное кубическим сплайном значение функции в точке x.

Кубическая интерполяция позволяет построить кривую, проходящую через заданные точки, таким образом, чтобы первые и вторые производные были бы непрерывными во всех точках. Такая кривая может быть построена разделением промежутка интерполяции на трехточечные интервалы, внутри которых записываются полиномы третьей степени, проходящие через эти точки. Эти полиномы затем соединяются вместе и образуют общую кривую.

Вектор v_s представляет собой вторые производные в заданных точках.Он возвращается оператором cspline(v_x,v_y). Применим оператор interp и cspline для нашей задачи в точках x=-0.5 и x=0.5.

Применение сплайн-интерполяции во всем промежутке дает кривую,

_,

показанную на рис.5.6.

Рис.5.6.Интерполяция данных обычным полиномом Lagr(zx),

сплайн-интерполяцией Intrp(zx),

кусочно-линейной функцией Linterp(zx).

Выводы

Пользуясь различными методами интерполяции, мы получили три разных набора данных, представленных в таблице 5.3.

Таблица 5.3

Результаты интерполяции, полученные различными методами

x	y
	Lagrang	linterp	interp
-1	0.333	0.333	0.333
-0.5	0.5	0.667	0.417
0	1.0	1.0	1.0
0.5	1.833	2.0	1.917
1	3	3	3

Различие результатов в точках интерполяции х=-0.5 и х=0.5 достаточно велико. При х=-0.5 разброс данных составляет 50% от их среднего значения. Среднее значение получается интерполяцией по формуле Лагранжа. При х=0.5 разброс данных несколько меньше и равен 8%. В этом случае среднее значение обеспечивается интерполяцией при помощи сплайнов.

В качестве результатов расчёта выберем данные, полученные интерполяцией по формуле Лагранжа. Они обеспечивают идеальную гладкость функции в узлах интерполирования и находятся в середине области разброса данных, полученных разными методами.

х=-0.5 y=0.5; x=0.5 y=1.833

Заметим, что зтот выбор не является универсальным. При невысоких требованиях к точности вместо результатов, полученных по формуле Лагранжа, можно использовать результаты, возвращаемые опрератором Mathcad linterp, а в случае большого числа узлов интерполяции, когда степень интерполяционного полинома становится слишком большой и затрудняет выполнение основных расчетов, и при высоких требованиях к точности нужно пользоваться оператором Маthcad interp или другими способами осуществления сплайн-интерполяции