48. Магнитное поле. Правило правого винта. Рамка с током ,вращающий момент. Силовые линии магнитного поля. Вектор магнитной индукции магнитного поля. Напряженность магнитного поля.

Силовое поле-магнитное. Наличие магнитного поля определяется по силовому действию на помещенные в него проводники с током или постоянные магниты. У магнитного поля имеет важнейшая особенность состоит в том, что оно оказывает силовое воздействие только на движущиеся в этом поле электрические заряды. Из опытов известно, что характер воздействия магнитного поля на ток меняется в зависимости от формы проводника, по которому течет ток, от расположения проводника относительно магнитного поля и от направления тока. Ориентация контура (рамка с током)в пространстве задается направлением нормали к контуру. Направление нормали задается правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, у которого головка вращается в направлении текущего в рамке тока. Опыты демонстрируют, что магнитное поле воздействует на рамку с током, поворачивая ее определенным образом, тем самым определяется направление внешнего магнитного поля. Рамку с током можно также использовать и для количественного описания магнитного поля. Поскольку на рамку с током воздействует магнитное поле и оказывает на рамку ориетирующее действие, то на нее в магнитном поле действует пара сил. Вращающий момент этих сил зависит как от свойств поля в данной точке, так и от свойств самой рамки и задается формулой М= [p_mB] ,где р- вектор магн. момента рамки с током.для плоского контура с током: р=ISn ,где n-един. Вектор нормали к поверх.рамки. Если в точку магнитного поля помещать рамки с различными магнитными моментами, то на них оказывают действие различные вращающие моменты, но при этом отношение Мmax/рm (Мmax — максимальный вращающий момент) для всех контуров одинаково и поэтому может служить характеристикой магнитного поля, которая называется магнитной индукцией: B= M_max/p_m. Магнитная индукция в данной точке однородного магнитного поля задается максимальным вращающим моментом, который действует на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Поскольку магнитное поле есть силовое поле, то его, по аналогии с электрическим, графически изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, который ввинчивают по направлению тока, вращается в направлении линий магнитной индукции. Магнитное поле токов описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим выражением: В=µ₀µН. μ — магнитная проницаемость среды

49. закон Био-Савара-Лапласа. Индукция прямого и кругового тока. Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке индукцию поля dB, равен : dB= где r- радиус-вектор..Направление dF перпенд. dl и r, т.е.перпенд.плоскости,в которой они лежат и совпадают с касательной к линии магнитной индукции. Это направ. Может быть найдено по правилуправого винта: направление вращения головки винта дает направление dF, если поступат. Движение винта соответс. Направлению тока в элементе. Принцип суперпозиции:магнитная индукция результир. Поля, создаваемого несколькими точками или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей,создаваемых каждым током или движущимся зарядом в отдельности. Магнитное поле прямого тока — тока, текущего по тонкому прямому бесконечному проводу. B = ; Магнитное поле в центре кругового проводника с током . Каждый элемент кругового проводника с током создает в центре магнитное поле одинакового направления - вдоль нормали от витка. Значит, сложение векторов dB также можно заменить сложением их модулей. B = ;

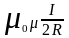50. сила Ампера. Взаимодействие токов.

Ампер установил, что сила dF , с которой магнитное поле действует на элемент проводника dl с током ,помещена в это поле: dF= I[dl,B].

Направление вектора dF можно найти по правилу левой руки: если ладонь руки расположить так, чтобы в нее входил вектор В, а 4е вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы равен: dF = . Закон Ампера применяют для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂,расстояние между которыми R. Направление вектора B₁ определяется правилом правого винта, направление силы тока по правилу левой руки…т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой dF = , если токи имеют противоположные направления, то, используя правило левой руки,можно сказать,что между ними действует сила отталкивания, определяемая формулой выше.