
- •390005, Рязань, ул. Гагарина, 59/1.
- •Обозначение координат и единичных векторов
- •Обозначения величин
- •1. Векторы Некоторые формулы векторной алгебры
- •Операции векторного анализа
- •Основные характеристики
- •Электрические токи
- •Векторы поля
- •3. Уравнения максвелла
- •Первое уравнение Максвелла – обобщение закона полного тока
- •Второе уравнение Максвелла обобщение закона электромагнитной индукции Фарадея
- •Третье уравнение Максвелла теорема о потоке вектора электрической индукции
- •Четвертое уравнение Максвелла закон непрерывности магнитного поля
- •4. Граничные условия
- •5. Теорема пойнтинга
- •6. Электростатическое поле
- •7 . Стационарное магнитное поле Основные уравнения стационарного магнитного поля
- •8. Электрическое поле в проводящей среде Основные уравнения электрического поля
- •9. Плоские электромагнитные волны
- •10. Волноводы
- •11. Объемные резонаторы
- •12. Элементарные излучатели
- •Приложения
- •Сводка применений дифференциального оператора
- •Основные единицы измерения физических величин
8. Электрическое поле в проводящей среде Основные уравнения электрического поля
Первый закон Кирхгофа
![]() ,
,
![]() .
.
Tок проводимости, протекающий через поверхность ,
![]() .
.
Закон Ома в дифференциальной форме
![]() .
.
Закон ДжоуляЛенца
![]() .
.
Разность потенциалов между двумя точками
![]() .
.
Задачи
8.1.
Вычислить шаговое напряжение
![]() для полусферического за-землителя.
Сила тока
=100
А; проводимость земли
=
10 -2
См/м; длина шага
=
0,8 м (рис. 8.1).
для полусферического за-землителя.
Сила тока
=100
А; проводимость земли
=
10 -2
См/м; длина шага
=
0,8 м (рис. 8.1).
Рис. 8.1
Рис. 8.2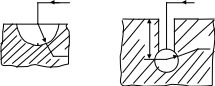
![]() сферического за-землителя радиусом
,
зарытого в землю на глубину
сферического за-землителя радиусом
,
зарытого в землю на глубину
![]() .
Удельная проводимость земли равна
.
Ток, текущий к заземлителю, равен
(рис. 8.2).
.
Удельная проводимость земли равна
.
Ток, текущий к заземлителю, равен
(рис. 8.2).
8.3. Вычислить плотность тока утечки и напряженность магнитного поля:
а) сферического конденсатора, заполненного диэлектриком с диэлектрической проницаемостью и проводимостью , если разность потенциалов между обкладками равна , а радиусы обкладок и ;
Рис. 8.3
![]()
![]()
8.4.
Вычислить плотность тока утечки и
мощность тепловых потерь плоского
двухслойного конденсатора, заполненного
диэлектриком с параметрами, указанными
на рис. 8.3. Площадь пластин конденсатора
.
Разность потенциалов между обкладками
равна
.
Краевым эффектом пренебречь. При
этом
![]() =3;
=10-8
См/м;
=
6;
=210-8
См/м;
=
=2
см;
=50
см2;
=120
В.
=3;
=10-8
См/м;
=
6;
=210-8
См/м;
=
=2
см;
=50
см2;
=120
В.
Рис. 8.4
8.6.
Определить ток утечки коаксиального
кабеля на 1 км длины. Пространство между
жилой и оболочкой заполнено неидеальным
диэлектриком с проводимостью
=10-10
См/м, радиус жилы
,
радиус оболочки
![]() (
основание натуральных логарифмов).
Напряжение между жилой и оболочкой 10
кВ.
(
основание натуральных логарифмов).
Напряжение между жилой и оболочкой 10
кВ.
Рис. 8.5
8.8.
Диэлектрик коаксиального кабеля имеет
удельную проводимость
См/м.
Разность потенциалов между внутренним
и внешним проводниками кабеля
.
Радиус внутреннего проводника
,
внутренний радиус трубы
(рис. 8.5). Найти сопротивление изоляции
отрезка кабеля длиной
,
ток утечки в том же отрезке, мощность
тепловых потерь. Построить кривую
![]() .
.
8.9. К плоскому конденсатору, расстояние между обкладками которого равно , а площадь каждой , подведено напряжение . Удельная проводимость диэлектрика . Найти сопротивление изоляции, ток утечки, мощность тепловых потерь, если = 5 мм; = 50 см2; =10 -10 См/м; =500 В.
