
- •390005, Рязань, ул. Гагарина, 59/1.
- •Обозначение координат и единичных векторов
- •Обозначения величин
- •1. Векторы Некоторые формулы векторной алгебры
- •Операции векторного анализа
- •Основные характеристики
- •Электрические токи
- •Векторы поля
- •3. Уравнения максвелла
- •Первое уравнение Максвелла – обобщение закона полного тока
- •Второе уравнение Максвелла обобщение закона электромагнитной индукции Фарадея
- •Третье уравнение Максвелла теорема о потоке вектора электрической индукции
- •Четвертое уравнение Максвелла закон непрерывности магнитного поля
- •4. Граничные условия
- •5. Теорема пойнтинга
- •6. Электростатическое поле
- •7 . Стационарное магнитное поле Основные уравнения стационарного магнитного поля
- •8. Электрическое поле в проводящей среде Основные уравнения электрического поля
- •9. Плоские электромагнитные волны
- •10. Волноводы
- •11. Объемные резонаторы
- •12. Элементарные излучатели
- •Приложения
- •Сводка применений дифференциального оператора
- •Основные единицы измерения физических величин
7 . Стационарное магнитное поле Основные уравнения стационарного магнитного поля
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
.
;
.
Закон
Био-Савара
![]() ,
где
линейный ток;
,
где
линейный ток;
![]()
длина элемента тока;
расстояние от элемента тока до точки,
в которой определяется
длина элемента тока;
расстояние от элемента тока до точки,
в которой определяется
![]() ;
;
![]()
единичный вектор, направленный от
элемента тока к точке, в которой
определяется
.
единичный вектор, направленный от
элемента тока к точке, в которой
определяется
.
Магнитный поток через поверхность , ограниченную контуром :
![]() .
.
Индуктивность витка с током, равным :
![]() .
.
Взаимная
индуктивность двух витков с токами
![]() и
и
![]() :
:
![]() ,
,
где
![]()
поток вектора
поток вектора
![]() ,
создаваемый током
через первый контур;
,
создаваемый током
через первый контур;
![]()
поток вектора
поток вектора
![]() ,
создаваемый током
через
второй контур.
,
создаваемый током
через
второй контур.
Задачи
7.1. Рассчитать напряженность магнитного поля на оси круглого плоского витка радиусом , по которому протекает ток (рис. 7.1).
Рис. 7.1
Рис. 7.2



![]()
![]()
![]()
![]() (рис. 7.2).
(рис. 7.2).
7.3. Рассчитать напряженность магнитного поля цилиндрической трубы, по которой протекает ток (рис. 7.3).
7.4.
Определить напряженность магнитного
поля на оси длинного соленоида,
содержащего
витков на единицу длины. Сила тока в
соленоиде
,
радиус витка
,
длина
![]() (рис. 7.4).
(рис. 7.4).
Рис. 7.3 Рис. 7.4
Рис. 7.5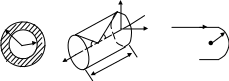
![]()
![]() 0
0
7.6.
В цилиндрическом проводнике радиусом
просверлен круглый канал радиусом
,
ось которого параллельна оси цилиндра
и расположена от нее на расстоянии
(![]() ).
По металлической части цилиндра течет
однородный ток, направленный вдоль
оси. Используя принцип суперпозиции,
найти величину и направление магнитного
поля в канале.
).
По металлической части цилиндра течет
однородный ток, направленный вдоль
оси. Используя принцип суперпозиции,
найти величину и направление магнитного
поля в канале.
7.7. Вычислить магнитную энергию, сосредоточенную внутри цилиндрического проводника единичной длины, по которому протекает ток . Магнитная проницаемость проводника . Построить .
а б
в
Р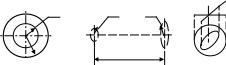
![]()
![]()

 ис.
7.6
ис.
7.6
7.9.
Три параллельных провода радиусом
расположены
так, что расстояния между ними равны
![]() ,
,
![]() ,
,
![]() .
Определить погонную взаимную индуктивность
.
Определить погонную взаимную индуктивность
![]() ,
,
![]() ,
т.е. петли 12 и петли 13 (рис. 7.7).
,
т.е. петли 12 и петли 13 (рис. 7.7).
7.10.
Рамка, на которую плотно намотано
витков провода, размещена вблизи
двухпроводной линии, как показано на
рис. 7.8. Определить ЭДС, наводимую в
линии, если по рамке течет ток
![]() .
Стороны рамки длиной
параллельны
проводам,
.
Стороны рамки длиной
параллельны
проводам,
![]() .
.
1 2 3
1
3
2
Рис. 7.7
Рис. 7.8
![]()
![]()
![]()
7.11. Определить взаимную индуктивность на 1 км длины двух параллельных двухпроводных линий передачи, провода которых расположены в углах квадрата со стороной 1 м.
7.12.
Полый медный провод имеет радиусы
и
![]() .
Определить собственную индуктивность
провода на единицу длины, полагая
плотность тока одинаковой по всему
сечению проводника.
.
Определить собственную индуктивность
провода на единицу длины, полагая
плотность тока одинаковой по всему
сечению проводника.
7.13. Проволочная рамка в форме равнобедренной трапеции находится в воздухе в одной плоскости с длинным проводом, по которому течет ток . Определить взаимную индуктивность между проводом и рамкой (рис. 7.9).
7.14. Определить индуктивность двухпроводной линии передачи длиной =10 км при расстоянии =2 м между проводами, считая, что по ним протекают равные токи в противоположных направлениях. Радиус проводов =6 мм.
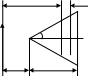
7.15. Определить взаимную индуктивность треугольной петли и бесконечного одиночного проводника с током (рис. 7.10).
Рис. 7.9
Рис. 7.10
50 0
Рис. 7.11
![]()
 2
2![]() 1
1
![]()

![]() =10
А/м. Угол между нормалью
рамки и вектором
составляет 50°. Определить момент пары
сил, действующих на рамку (рис. 7.11).
=10
А/м. Угол между нормалью
рамки и вектором
составляет 50°. Определить момент пары
сил, действующих на рамку (рис. 7.11).
1 2
4 3
Рис. 7.12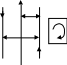
7.18. Определить взаимную индуктивность двухпроводной линии и рамки, лежащей в плоскости линии (рис. 7.12).
7.19.
Определить индуктивность катушки из
витков, намотанных на тороид. Магнитная
проницаемость материала тороида равна
![]() и значительно превышает магнитную
проницаемость внешней среды (рис.
7.13).
и значительно превышает магнитную
проницаемость внешней среды (рис.
7.13).
Рис. 7.13
Рис. 7.14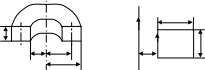
![]() от прямолинейного бесконечного
проводника, протекает ток
от прямолинейного бесконечного
проводника, протекает ток
![]() .
Вычислить ЭДС в проводнике
(рис. 7.14).
.
Вычислить ЭДС в проводнике
(рис. 7.14).
