
- •390005, Рязань, ул. Гагарина, 59/1.
- •Обозначение координат и единичных векторов
- •Обозначения величин
- •1. Векторы Некоторые формулы векторной алгебры
- •Операции векторного анализа
- •Основные характеристики
- •Электрические токи
- •Векторы поля
- •3. Уравнения максвелла
- •Первое уравнение Максвелла – обобщение закона полного тока
- •Второе уравнение Максвелла обобщение закона электромагнитной индукции Фарадея
- •Третье уравнение Максвелла теорема о потоке вектора электрической индукции
- •Четвертое уравнение Максвелла закон непрерывности магнитного поля
- •4. Граничные условия
- •5. Теорема пойнтинга
- •6. Электростатическое поле
- •7 . Стационарное магнитное поле Основные уравнения стационарного магнитного поля
- •8. Электрическое поле в проводящей среде Основные уравнения электрического поля
- •9. Плоские электромагнитные волны
- •10. Волноводы
- •11. Объемные резонаторы
- •12. Элементарные излучатели
- •Приложения
- •Сводка применений дифференциального оператора
- •Основные единицы измерения физических величин
6. Электростатическое поле
Система
уравнений электростатики
частный случай системы уравнений
Максвелла, когда
![]() =0:
=0:
![]() ;
;
![]() ;
;
![]() ;
.
;
.
Для
описания электростатического поля
вводится скалярная функция
потенциал
:
![]() .
.
Введенный таким образом потенциал неоднозначен и не имеет физического смысла.
Разность потенциалов между двумя точками численно равна работе по перемещению единичного положительного заряда между ними:
![]() .
.
Эта величина не зависит от пути, по которому перемещался заряд.
Как следует из вышеприведенных формул, понятие разности потенциалов является точным лишь для полей, не зависящих от времени.
Граничные условия электростатики у поверхности проводника
![]() ;
;
![]() .
.
Таким образом, поверхность проводника в электростатическом поле эквипотенциальна.
Энергия
электростатического поля
![]() ,
где
объем заряженного тела;
потенциал относительно бесконечно
удаленной точки.
,
где
объем заряженного тела;
потенциал относительно бесконечно
удаленной точки.
Емкость
заряженного тела определяется как
коэффициент пропорциональности
между его потенциалом относительно
бесконечно удаленной точки и зарядом,
сосредоточенным на этом теле:
![]() .
.
Конденсатор
представляет собой систему двух
проводников, несущих равные по
величине и противоположные по знаку
заряды. Его емкость
![]() ,
где
,
где
![]()
величина заряда одного из тел;
величина заряда одного из тел;
![]()
разность потенциалов между ними.
разность потенциалов между ними.
Задачи
Рис. 6.1
![]()
![]()
![]() .
Является ли данная функция решением
уравнения Лапласа?
.
Является ли данная функция решением
уравнения Лапласа?
6.2.
На внутренней сфере расположен заряд
![]() ,
Вычислить поверхностную плотность
заряда и полный заряд внешней сферы,
выполненной из идеального проводника
(рис. 6.1).
,
Вычислить поверхностную плотность
заряда и полный заряд внешней сферы,
выполненной из идеального проводника
(рис. 6.1).
6.3. Определить радиус уединенной сферы емкостью 1 Ф. Среда вакуум.
6.4.
Заряд с объемной плотностью
![]() распределен
в объеме шара радиусом
.
Определить закон изменения напряженности
и индукции электрического поля внутри
и вне шара. Описать поведение векторов
и
при переходе
границы шар-воздух. Вычислить энергию
электрического поля, создаваемую
заряженным шаром. Диэлектрическая
проницаемость материала шара
,
среды
.
распределен
в объеме шара радиусом
.
Определить закон изменения напряженности
и индукции электрического поля внутри
и вне шара. Описать поведение векторов
и
при переходе
границы шар-воздух. Вычислить энергию
электрического поля, создаваемую
заряженным шаром. Диэлектрическая
проницаемость материала шара
,
среды
.
Рис. 6.2
![]() и
и
![]() ,
заполняющих двухслойный сферический
конденсатор, имеющий заряд
(рис. 6.2).
,
заполняющих двухслойный сферический
конденсатор, имеющий заряд
(рис. 6.2).



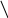
![]()
![]()

 Рис. 6.3
Рис. 6.3 .6.
Определить погонную емкость, разность
потенциалов между обкладками, напряженность
поля и индукцию в диэлектрике,
заполняющем двухслойный цилиндрический
конденсатор. На единицу длины
конденсатора приходится заряд
(рис. 6.3).
.6.
Определить погонную емкость, разность
потенциалов между обкладками, напряженность
поля и индукцию в диэлектрике,
заполняющем двухслойный цилиндрический
конденсатор. На единицу длины
конденсатора приходится заряд
(рис. 6.3).
6.7.
Положительный заряд равномерно
распределен по кольцевой линии радиусом
.
Диэлектрическая проницаемость среды
.
Линейная плотность заряда
.
Найти потенциал и напряженность поля
в точках, лежащих на оси кольца. Построить
![]() и
и
![]() (рис. 6.4).
(рис. 6.4).
6.8.
Положительный заряд
равномерно распределен на плоском
круглом диске радиусом
.
Диэлектрическая проницаемость среды
,
диска
![]() .
Найти напряженность электрического
поля
и потенциал
точек, лежащих на оси
,
нормальной к диску и проходящей через
ее центр, если
=
10 -6
Кл,
=10
см (рис. 6.5).
.
Найти напряженность электрического
поля
и потенциал
точек, лежащих на оси
,
нормальной к диску и проходящей через
ее центр, если
=
10 -6
Кл,
=10
см (рис. 6.5).
0
Рис. 6.4
Рис. 6.5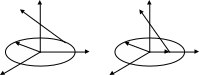
![]()
Рис. 6.6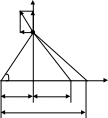
![]()
![]()
![]()
![]() =1
мм:
=8,8910-11
Кл. Шар находится в воздухе.
=1
мм:
=8,8910-11
Кл. Шар находится в воздухе.
6.11. Начало декартовых координат помещено в геометрическом центре заряженного проводящего шара. Найти заряд шара, если разность потенциалов точек А(-14, 4, 8) и В(-12, 16, 0) (в см) равна 30 В, а радиус шара =2 мм.
6.12.
Непосредственным интегрированием,
используя теорему Гаусса, показать, что
напряженность электрического поля на
расстоянии
от бесконечного тонкого провода
![]() ,
где
линейная плотность заряда.
,
где
линейная плотность заряда.
6.13.
Даны три заряженные сферы радиусом
.
Одна из них проводящая, другая
однородно заряжена по всему объему, а
по объему третьей заряд распределен
сферически симметрично, причем плотность
заряда меняется как
![]() .
Полный заряд каждой сферы
.
Пользуясь теоремой Гаусса, найти
электрическое поле внутри и вне каждой
сферы. Построить графики зависимости
поля от радиуса. Для третьего случая
принять
=
-2,
=2.
.
Полный заряд каждой сферы
.
Пользуясь теоремой Гаусса, найти
электрическое поле внутри и вне каждой
сферы. Построить графики зависимости
поля от радиуса. Для третьего случая
принять
=
-2,
=2.
Рис. 6.7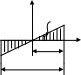
![]() ,
где
и
главные радиусы кривизны поверхности.
,
где
и
главные радиусы кривизны поверхности.
6.15.
Заряд распределен на нити с линейной
плотностью
![]() .
Определить
потенциал на оси
.
Определить
потенциал на оси
![]() (рис.
6.7).
(рис.
6.7).
Рис. 6.8
![]()
![]()
![]()
![]() равномерно распределен между двумя
концентрическими сферическими
поверхностями. Радиус внешней поверхности
,
радиус внутренней поверхности
.
Диэлектрическая проницаемость среды
между шаровыми поверхностями
,
окружающей среды
(рис. 6.8). Найти
равномерно распределен между двумя
концентрическими сферическими
поверхностями. Радиус внешней поверхности
,
радиус внутренней поверхности
.
Диэлектрическая проницаемость среды
между шаровыми поверхностями
,
окружающей среды
(рис. 6.8). Найти
![]() ,
,
![]() ,
,
![]() .
Построить графики поля.
.
Построить графики поля.
Рис. 6.9







![]()
![]()
![]()
![]()
6.18.
Металлический шар радиусом 0,2 м
несет на себе заряд
=610-5
Кл. Диэлектрическая проницаемость
среды
![]() .
Подсчитать энергию электрического
поля.
.
Подсчитать энергию электрического
поля.
Рис. 6.10
6.20. Определить силы, действующие на обкладки плоского конденсатора площадью , если:
Рис. 6.11
![]()
б) конденсатор подключен к источнику .
6.21. Три заряда расположены, как показано на рис 6.11. Вычислить электростатическую силу, действующую на каждый заряд. Вычислить полную потенциальную энергию системы зарядов.
6.22.
Найти распределение зарядов, создающих
в вакууме потенциал
![]() .
.
6.23. Вычислить энергию равномерно заряженного шара радиусом . Диэлектрическая проницаемость шара , заряд , окружающая среда вакуум.
Рис. 6.12![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 .24.
Вывести формулы для определения
напряженности поля и емкости
двухслойного плоского конденсатора, а
также построить графики изменения
модулей векторов напряженности
электрического поля, модуля вектора
электрической индукции
и потенциала
в функции расстояния
.
Толщина первого слоя
диэлектрика
,
второго слоя
.
Диэлектрическая проницаемость первого
слоя
.24.
Вывести формулы для определения
напряженности поля и емкости
двухслойного плоского конденсатора, а
также построить графики изменения
модулей векторов напряженности
электрического поля, модуля вектора
электрической индукции
и потенциала
в функции расстояния
.
Толщина первого слоя
диэлектрика
,
второго слоя
.
Диэлектрическая проницаемость первого
слоя
![]() ,
второго
.
Принять
,
второго
.
Принять
![]() ;
;
![]() .
Разность потенциалов между обкладками
конденсатора равна
.
Площадь пластин конденсатора
(рис. 6.12).
.
Разность потенциалов между обкладками
конденсатора равна
.
Площадь пластин конденсатора
(рис. 6.12).
