3. Уравнения максвелла
Классическая теория электромагнетизма основывается на уравнениях Максвелла, являющихся обобщением опытных данных, полученных при изучении электромагнитных явлений.
Первое уравнение Максвелла – обобщение закона полного тока
Рис. 3.1
,
где
объемная плотность тока проводимости;
объемная плотность стороннего тока;
вектор электрического смещения.
Дифференциальная форма записи этого уравнения имеет вид
,
где
объемная плотность смещения.
Введение тока смещения связало уравнения Максвелла в систему, решением которой в общем случае является электромагнитная волна.
Второе уравнение Максвелла обобщение закона электромагнитной индукции Фарадея
Циркуляция
вектора напряженности электрического
поля
по замкнутому контуру
равна скорости изменения магнитного
потока
,
взятой с обратным знаком:
.
При
изменении магнитной индукции
или деформации и перемещении
проводящего контура
в нем возникает ЭДС индукции.
Дифференциальная форма записи этого
уравнения
.
Изменение
магнитного поля во времени (
)
вызывает появление вихревого электрического
поля в пространстве.
Третье уравнение Максвелла теорема о потоке вектора электрической индукции
Рис. 3.2
,
где объемная плотность заряда; внешняя нормаль к поверхности.
Дифференциальная
форма записи этого уравнения
.
Источником силовых линий электрического
поля являются электрические заряды.
Четвертое уравнение Максвелла закон непрерывности магнитного поля
Поток
вектора магнитной индукции
через замкнутую поверхность
равен нулю:
.
В
дифференциальной форме
.
В природе нет магнитных зарядов,
которые являлись бы источниками или
стоками силовых линий магнитного поля,
поэтому магнитные силовые линии поля
всегда замкнуты.
К
основным принципам электродинамики
относится закон сохранения заряда
или
.
Минус обозначает, что при вытекании
тока из объема заряд в последнем
уменьшается.
Дифференциальная форма записи этого уравнения:
.
Материальные
уравнения:
,
.
Обобщенный
закон Ома:
,
где
удельная
проводимость среды.
Задачи
3.1.
Определить циркуляцию векторов
и
по контуру с координатами (0, 0); (0, 1); (1,
1); (1, 0), если плотность тока проводимости
,
плоскости
;
плотность тока смещения
;
.
3.2.
Определить циркуляцию векторов
и
по контуру (см. 3.1), если объемная плотность
тока проводимости
,
а вектор электрического смещения
.
3.3.
Квадратная рамка со стороной
=
1 м находится в поле
.
Магнитная проницаемость среды
,
плоскость рамки перпендикулярна к
.
Определить ЭДС, наведенную в рамке.
3.4.
Дано
.
Доказать,
что для переменных во времени полей в
однородной изотропной среде без свободных
токов и зарядов
.
Считая
,
показать, что
.
+ + + +
+ + +
+
Рис. 3.3
3.6.
Вычислить напряженность магнитного
поля
,
где
расстояние от оси прямолинейного
бесконечного проводника, по которому
протекает ток
.
Рис. 3.4
.
Вычислить плотность тока смещения и
величину тока во внешней цепи, если
площадь пластин
,
а расстояние между пластинами при
=
0 равно
.
Краевой эффект не учитывать.
3.8.
В однородном магнитном поле с напряженностью
вращается прямоугольная плоская рамка
со скоростью
.
Длина сторон равна
и
,
число витков
,
магнитная проницаемость среды
,
число оборотов в секунду. Вычислить ЭДС
в рамке (рис. 3.4).
3.9.
Напряженность поля в некоторой области
меняется по закону
,
,
;
.
Найти объемную плотность заряда в данной
области, если
.
3.10.
Некоторое тело с диэлектрической
проницаемостью
и проводимостью
в момент
времени
имеет плотность заряда
.
Oпpeделить,
за какое время во внутренней части тела
объемная плотность заряда
уменьшится вдвое. Нарушается ли закон
сохранения заряда?
3.11. Задано поле :
где радиус-вектор. Найти распределение зарядов, образовавших такое поле.
3.12.
В некоторой области с диэлектрической
проницаемостью
задано поле
.
Вычислить объемную плотность заряда.
3.13.
В проводящей среде с проводимостью
=
8 См/м постоянный ток создает магнитное
поле
.
Определить электрическое поле
в среде.
3.14.
Задано поле
.
Показать, что оно не может быть ни
электрическим, ни магнитным.
3.15.
В свободном пространстве (
)
задано электромагнитное поле своими
составляющими
,
.
При каких значениях
и
это поле удовлетворяет уравнениям
Максвелла.
3.16.
Показать, что электромагнитное поле в
вакууме
,
,
ни
при каких
и
не удовлетворяет уравнениям Максвелла.
Рис. 3.5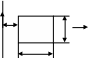
=
0,02 А/м. Можно ли построить прибор,
измеряющий таким образом скорость
самолета?
3.18. По бесконечному прямолинейному проводнику протекает постоянный ток . Плоская рамка (рис. 3.5) удаляется от проводника со скоростью . Вычислить ЭДС в рамке, если число витков в ней равно , а параметры среды , .
3.19.
При какой частоте отношение плотностей
токов смещения и проводимости в меди
(
=5,7107
См/м,
) будет таким же, как и в сухой почве (
=
10-4
См/м,
=
2
)
на частоте
=
103
Гц?
3.20.
Определить частоту
,
при которой амплитуды объемной плотности
тока смещения и плотности тока проводимости
будут равны:
1)
среда
медь (
=57106
См/м;
=1);
2) среда
морская вода (
=4
См/м;
=80);
3) среда
фарфор (
=10-13
См/м;
=
6).
3.21.
Вычислить, на какой частоте плотности
токов смещения и проводимости будут
одинаковыми в среде с
=10-2
См/м,
.
+ +
+ +
+
+ + +
+ +
+ +
Рис. 3.6
3.23.
По прямолинейному проводнику протекает
ток
(рис. 3.7). Вычислить ЭДС, наведенную в
рамке, состоящей из 10 витков, если
=
0,5 м;
=5
см;
=10
см;
=1
A;
=103
1/с. Паpаметpы окружающей сpеды:
,
.
+ + + +
+ + + +
+ + + +
Рис. 3.8
Рис. 3.7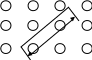
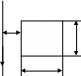.24.
Металлический стержень длиной
вращается с угловой скоростью
в однородном магнитном поле
.
Вычислить ЭДС в стержне (рис. 3.8).