11. Объемные резонаторы

Объемным резонатором называют часть пространства, ограниченную металлической поверхностью. Возможность построения таких систем вы­текает из уравнений Максвелла, согласно которым переменное электрическое поле является источником магнитного поля и, наоборот, переменное магнитное поле является источником электрического, т. е. обмен энергиями между электрическими и магнитными полями происходит непрерывно в любой области пространства. В изолированном от внешнего пространства объеме, заполненном средой без потерь, этот обмен будет протекать сколь угодно долго. Иначе говоря, в объеме будет существовать незатухающий колебательный процесс. Условием резонанса является равенство электрической и магнитной энергий .

Конфигурация объемного резонатора может быть различной. Простейшие из них представляют короткозамкнутые отрезки волноводов прямоугольного или круглого сечения. Структура полей в таких резонатоpax, как и в волноводах, определяется путем решения краевой задачи, полученного на основе однородного волнового уравнения Гельмгольца и соответствующих граничных условий, которые должны выполняться на стенках резонатора, включая торцевые. В таких резонаторах могут существовать колебания типа (для них =0) и типа (для них =0).

Поле в таких резонаторах можно рассматривать как суперпозицию двух волноводных волн, движущихся навстречу друг, а затем потребовать обращения в ноль поперечной составляющей электрического поля на торцевых стенках резонатора, т.е.

при и .

Эти условия позволяют определить длину резонатора

,

где =1, 2, 3,...  число полуволн, укладывающихся вдоль резонатора;  длина волны в волноводе;  продольное волновое число волноводной волны.

Для колебаний в прямоугольном резонаторе продольная состав­ляющая определяется соотношением

.

Для колебаний соответственно

.

Если учесть, что длина волны в волноводе , критическая длина волны и длина волны задающего генератора связаны дисперсионным соотношением

,

то резонансная длина волны определится следующим образом:

.

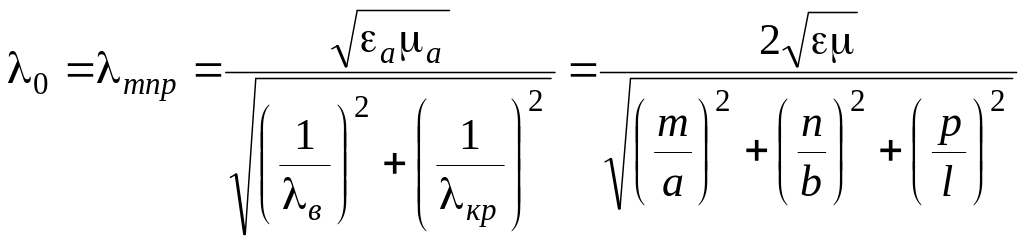Добротность объемного резонатора определяется соотношением

,

где  энергия, запасенная в резонаторе;  средняя за период мощность тепловых потерь.

Основным типом колебаний в прямоугольном резонаторе является коле­бание с резонансной длиной волны

при .

Величина энергии электромагнитного поля и добротность резонатора для колебаний типа определяются соотношениями

;

,

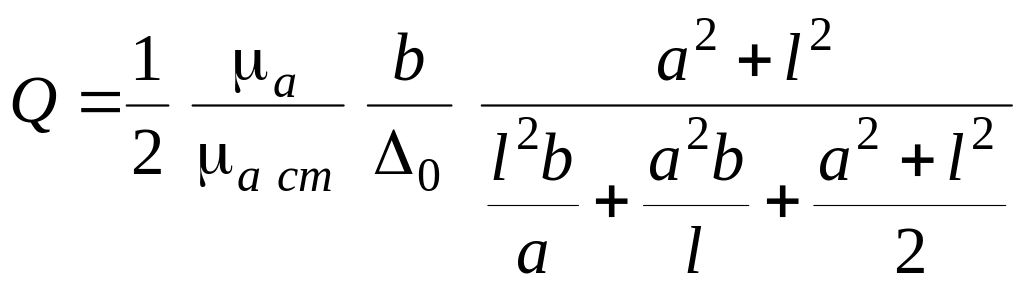где  глубина проникновения поля;  магнитная проницаемость материала стенок.

Для цилиндрического резонатора основным типом колебаний являются колебания , продольная составляющая этого типа колебаний ра­вна

.

Резонансная длина волны при

.

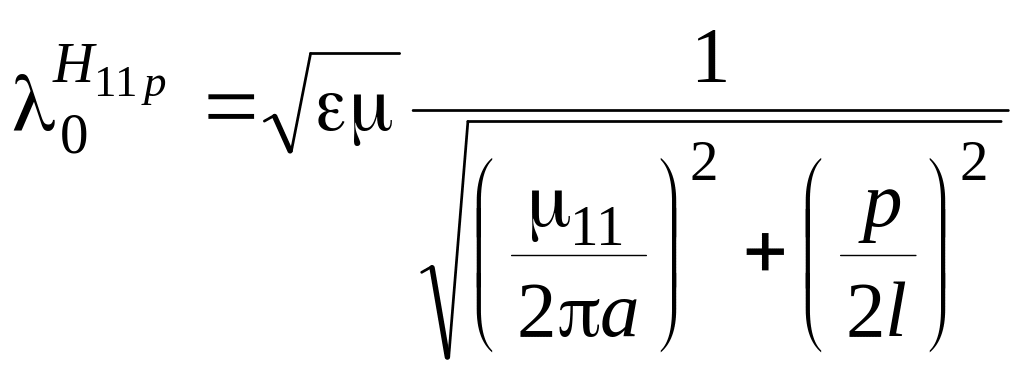Низшим типом колебаний среди колебаний являются колебания . Продольная составляющая колебаний типа определяется соотношением

.

Резонансная длина волны соответственно

.

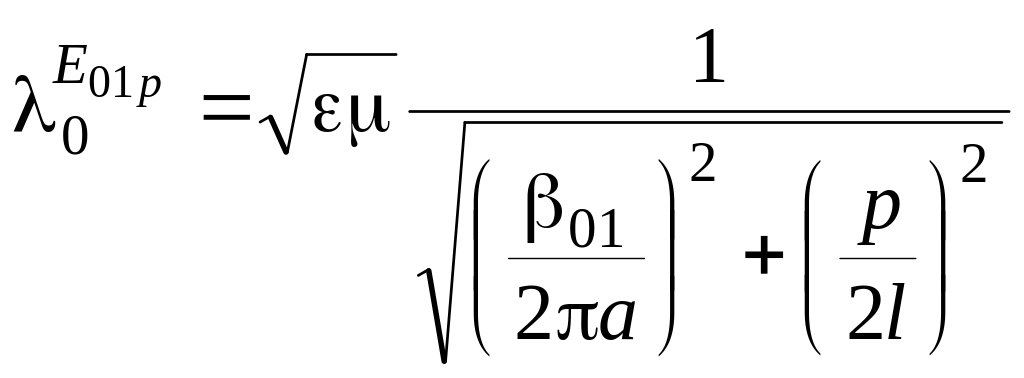Задачи

11.1. Вычислить первые 4 резонансные частоты прямоугольного резонатора со сторонами =1 см; =2,3; =4 см.

11.2. Прямоугольный объемный резонатор с колебаниями типа настроен на некоторую частоту . Можно ли настроить резонатор на эту частоту, если размер удвоить? На сколько нужно изменить , чтобы можно было настроить резонатор на частоту при волне ?

11.3. Вычислить резонансную длину волны резонатора с размерами =3 см; =1,см; =3 см. Стенки сверхпроводящие, заполнение  диэлектрик с параметрами =0; ; .

11.4. Определить резонансную частоту в цилиндрическом объемном резонаторе при типе колебаний , если диаметр основания 10 см, а высота 8 см.

11.5. Определить резонансную частоту прямоугольного объемного резонатора при типе колебаний , если размеры резонатора 2х2х3 см³.

11.6. Определить резонансную частоту в цилиндрическом объемном резонаторе при типе колебаний , если диаметр основания резонатора 3 см, а длина 2 см.

11.7. Определить, при каком отношении резонансные часто­ты колебаний типов и в цилиндрическом резонаторе равны. Ка­ково отношение резонансных частот этих колебаний при значениях вдвое меньших и вдвое больших найденного?

11.8. Вычислить резонансную частоту и собственную добротность (по точной и приближенной формулам) прямоугольного медного резона­тора при = =20 мм, =10 мм для колебаний типа . Шеро­ховатость стенок учитывается множителем =1,2.

11.9. Изобразить структуру поля в цилиндрическом объемном резонаторе.

11.10. Рассчитать добротность прямоугольного объемного резонатора с волной на частоте =9400 МГц (стенки резонатора изготовлены из меди).

11.11. Рассчитать добротность цилиндрического объемного резонатора с волной на частоте =9000 МГц (металл стенок резонатора  медь).

11.12. B прямоугольном объемном резонаторе, выполненном в виде куба с ребром , с помощью штыря, параллельного оси , возбуждается на резонансной частоте колебание типа . Координаты штыря ( , , 0). Какие типы колебаний будут возбуждаться в резо­наторе, если штырь направить параллельно оси (координаты основа­ния штыря 0, , ), параллельно оси у (координаты основания штыря , 0, )?

11.13. Указать оптимальное расположение штыря для возбуждения колебаний типа в цилиндрическом объемном резонаторе.

11.14. Каким образом должна быть прорезана щель на боковой стенке, чтобы возбудить колебание типа в цилиндрическом объем­ном резонаторе?