
- •390005, Рязань, ул. Гагарина, 59/1.
- •Обозначение координат и единичных векторов
- •Обозначения величин
- •1. Векторы Некоторые формулы векторной алгебры
- •Операции векторного анализа
- •Основные характеристики
- •Электрические токи
- •Векторы поля
- •3. Уравнения максвелла
- •Первое уравнение Максвелла – обобщение закона полного тока
- •Второе уравнение Максвелла обобщение закона электромагнитной индукции Фарадея
- •Третье уравнение Максвелла теорема о потоке вектора электрической индукции
- •Четвертое уравнение Максвелла закон непрерывности магнитного поля
- •4. Граничные условия
- •5. Теорема пойнтинга
- •6. Электростатическое поле
- •7 . Стационарное магнитное поле Основные уравнения стационарного магнитного поля
- •8. Электрическое поле в проводящей среде Основные уравнения электрического поля
- •9. Плоские электромагнитные волны
- •10. Волноводы
- •11. Объемные резонаторы
- •12. Элементарные излучатели
- •Приложения
- •Сводка применений дифференциального оператора
- •Основные единицы измерения физических величин
10. Волноводы
Волноводом называют полую металлическую трубу произвольного поперечного сечения. Наиболее часто используют прямоугольные или цилиндрические (круглые) волноводы. Ось волновода, как правило, совмещают с осью . Электромагнитное поле направляемой вдоль волновода волны представляют в виде
![]() ,
,
![]() ,
(10.1)
,
(10.1)
где
![]()
продольное волновое число.
продольное волновое число.
Электромагнитные
волны в регулярных волноводах не
являются поперечными. Различают
электрические или
-волны,
имеющие продольную составляющую
электрического поля
![]() (
(![]() =0),
и магнитные или
-волны,
имеющие продольную составляющую
магнитного поля
(
=0).
С учетом из уравнений Максвелла и (10.1)
все поперечные составляющие векторов
поля могут быть выражены через продольные;
для случая прямоугольного волновода
эта связь представляется в виде
=0),
и магнитные или
-волны,
имеющие продольную составляющую
магнитного поля
(
=0).
С учетом из уравнений Максвелла и (10.1)
все поперечные составляющие векторов
поля могут быть выражены через продольные;
для случая прямоугольного волновода
эта связь представляется в виде
![]() ,
,
![]() ,
(10.2)
,
(10.2)
![]() ,
,
![]() .
.
Здесь
![]()
поперечное волновое число, связанное
с продольным волновым числом
соотношением
поперечное волновое число, связанное
с продольным волновым числом
соотношением
![]() .
(10.3)
.
(10.3)
Полагая,
что в (10.2)
=0,
получают поперечные составляющие
векторов
и
для
волн
![]() ;
полагая
=
0, получают соответственно поперечные
составляющие для волн
;
полагая
=
0, получают соответственно поперечные
составляющие для волн
![]() .
.
Продольные составляющие полей в регулярном волноводе получаются на основе решения однородного волнового уравнения Гельмгольца при соответствующих граничных условиях. Для волн
![]() при
при
![]() ,
(10.4)
,
(10.4)
для волн
![]() при
при
![]() .
(10.5)
.
(10.5)
Отличные
от нуля решения записанной выше краевой
задачи получаются лишь при строго
определенных значениях
![]() ,
которые называются собственными
значениями данной краевой задачи. Они
определяются только формой и размерами
поперечного сечения волновода. В общем
случае результирующее поле в волноводе
представляет собой бесчисленную сумму
волн всех возможных типов.
,
которые называются собственными
значениями данной краевой задачи. Они
определяются только формой и размерами
поперечного сечения волновода. В общем
случае результирующее поле в волноводе
представляет собой бесчисленную сумму
волн всех возможных типов.
Электромагнитная
волна может распространяться в волноводе
и эффективно переносить энергию, если
частота
задающего генератора превышает некоторое
критическое значение
![]() ,
называемое критической частотой,
т.е. при условии
,
называемое критической частотой,
т.е. при условии
>
или
![]() .
(10.6)
.
(10.6)
Критическая
длина волны
![]() связана с критическим значением
волнового числа
связана с критическим значением
волнового числа
![]() ,
которое по величине совпадает с
собственным значением рассматриваемой
краевой задачи
,
которое по величине совпадает с
собственным значением рассматриваемой
краевой задачи
![]() соотношением
соотношением
![]() .
(10.7)
.
(10.7)
Продольное волновое число с учетом (10.3) равно
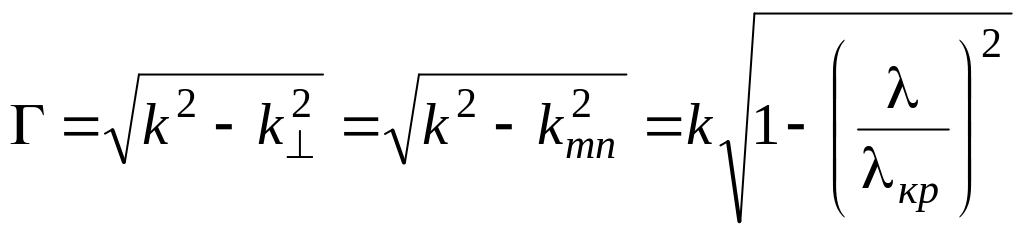 .
(10.8)
.
(10.8)
Длина волны в волноводе
![]() .
(10.9)
.
(10.9)
Фазовая скорость волны в волноводе
![]() ,
(10.10)
,
(10.10)
где
![]() есть скорость плоской однородной волны,
распространяющейся в безграничной
однородной среде с параметрами среды
,
,
заполняющей
волновод.
есть скорость плоской однородной волны,
распространяющейся в безграничной
однородной среде с параметрами среды
,
,
заполняющей
волновод.
Групповая скорость определяется соотношением
![]() .
(10.11)
.
(10.11)
Соотношения (10.7)(10.11) справедливы для регулярных волноводов любых сечений.
Для прямоугольного волновода
![]() ,
(10.12)
,
(10.12)
где
![]()
размеры широкой и узкой стенок волновода;
размеры широкой и узкой стенок волновода;
![]()
индексы волны, равные числу полуволн,
укладывающихся вдоль соответственно
широкой и узкой стенок волновода.
индексы волны, равные числу полуволн,
укладывающихся вдоль соответственно
широкой и узкой стенок волновода.
Для волн продольная составляющая электрического поля получается на основании решения краевой задачи (10.2) и имеет вид
![]() .
(10.13)
.
(10.13)
Поперечные
составляющие поля
![]() и
и
![]() для этого типа волны получаются из
(10.2) при условии
для этого типа волны получаются из
(10.2) при условии
![]() .
.
Характеристическое сопротивление волновода для волн типа
![]() ,
(10.14)
,
(10.14)
где
![]()
сопротивление среды, заполняющей
волновод.
сопротивление среды, заполняющей
волновод.
Для волн продольная составляющая магнитного поля получается на основании решения краевой задачи (10.5) и имеет вид
![]() .
(10.15)
.
(10.15)
Поперечные
составляющие поля
и
для этого типа волны получаются из
(10.2) при условии
![]() .
.
Характеристическое сопротивление волновода для волн типа
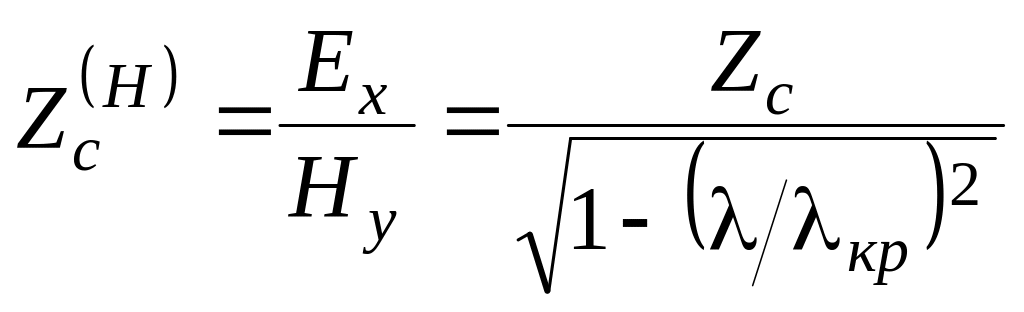 ,
(10.16)
,
(10.16)
Основной
волной в волноводе называют волну,
обладающую наибольшей критической
длиной. Такой волной для прямоугольного
волновода является волна
![]() .
Структура ее получается из общих
соотношений при значении индексов
.
Структура ее получается из общих
соотношений при значении индексов
![]() и
и
![]() .
Критическая длина волны для волны
равна
.
Критическая длина волны для волны
равна
![]() .
(10.17)
.
(10.17)
Если потребовать выполнения условий
![]() ,
,
![]() ,
(10.18)
,
(10.18)
то в волноводе будет распространяться только основная волна, волна ; для всех остальных типов волн
![]() .
.
Мощность, передаваемая по волноводу при распространении в нем основной волны, определяется соотношением
![]() ,
(10.19)
,
(10.19)
где
![]()
максимальное значение напряженности
электрического поля в точке
максимальное значение напряженности
электрического поля в точке
![]() .
.
Для волновода с потерями передаваемая мощность
![]() ,
(10.20)
,
(10.20)
где коэффициент затухания.
Для волны
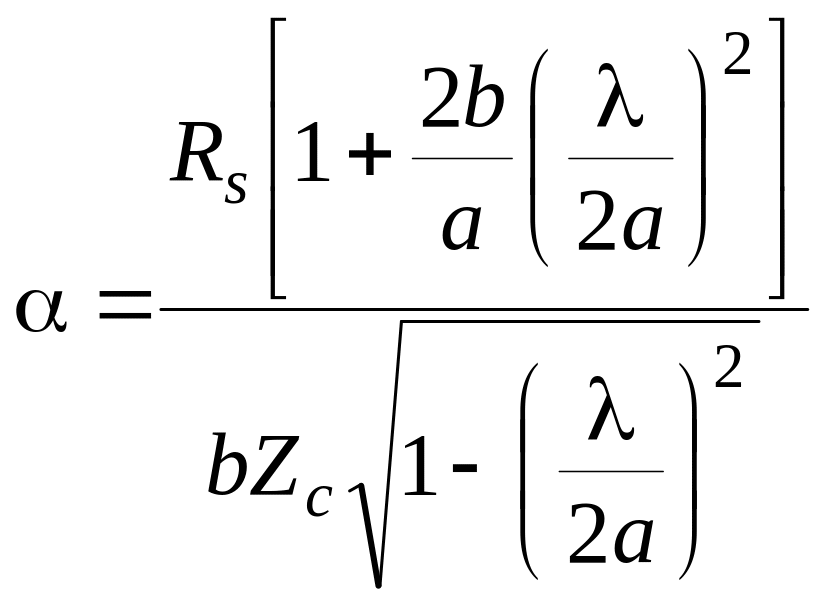 .
(10.21) Здесь
поверхностное сопротивление материала
стенок волновода.
.
(10.21) Здесь
поверхностное сопротивление материала
стенок волновода.
Для круглого волновода структура электромагнитного поля волн, распространяющихся по волноводу, определяется также на основе решения краевых задач (10.4) и (10.5) только в цилиндрической системе координат. Все поперечные составляющие, как и в случае прямоугольного волновода, выражаются через продольные; при этом надо исходить из уравнений Максвелла в цилиндрической системе координат. Эта связь представляется в виде:
 (10.22)
(10.22)
Полагая в них =0, получаем поперечные составляющие для волн ; полагая =0, получаем соответственно поперечные составляющие для волн .
Для волн собственные значения краевой задачи (10.4) получаются равными
![]() ,
(10.23)
,
(10.23)
где
радиус поперечного сечения волновода;
![]()
-й
корень уравнения
-й
корень уравнения
![]() ;
;
![]()
функция Бесселя
-го
порядка. Индексы
и
характеризуют число вариаций поля по
координатам
и
круглого волновода соответственно.
функция Бесселя
-го
порядка. Индексы
и
характеризуют число вариаций поля по
координатам
и
круглого волновода соответственно.
Критическая длина волны
![]() .
(10.24)
.
(10.24)
Продольная составляющая электрического поля
![]() .
(10.25)
.
(10.25)
Коэффициент затухания для волн
 .
(10.26)
.
(10.26)
Для волн типа собственные значения получаются равными
![]() ,
(10.27)
,
(10.27)
где
![]()
-й
корень уравнения
-й
корень уравнения
![]() ;
;
![]()
производная функции Бесселя.
производная функции Бесселя.
Критическая длина волны
![]() .
(10.28)
.
(10.28)
Продольная составляющая магнитного поля
![]() .
(10.29)
.
(10.29)
Коэффициент затухания для волн
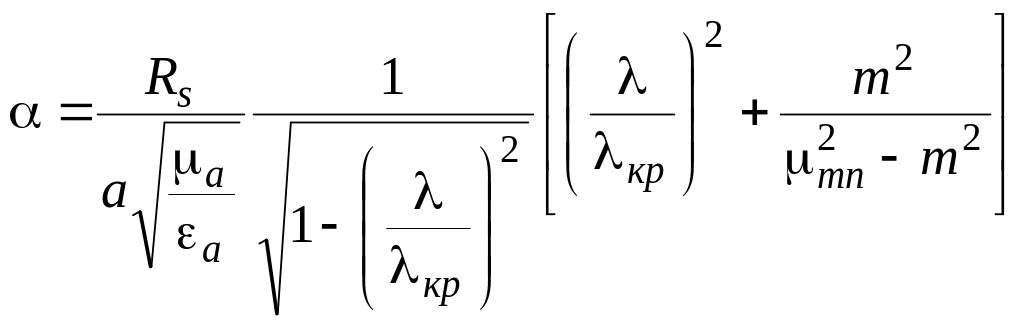 .
(10.30)
.
(10.30)
Основной
волной в круглом волноводе является
волна
![]() .
Ее структура может быть получена из
общих соотношений при значении индексов
=1
и
=1.
.
Ее структура может быть получена из
общих соотношений при значении индексов
=1
и
=1.
Критическая длина волны
![]() .
(10.31)
.
(10.31)
Если потребовать выполнения условий
![]() ,
(10.32)
,
(10.32)
то в волноводе будет распространяться волна ; для всех остальных типов волн .
Задачи
10.1.
Построить графики зависимостей
![]() и
от
и
от
![]() для волны
основного типа заполненного воздухом
волновода, если
размер широкой стенки волновода.
для волны
основного типа заполненного воздухом
волновода, если
размер широкой стенки волновода.
10.2.
Как изменятся результаты задачи 10.1 при
заполнении волновода диэлектриком
с
![]() ?
?
10.3. Показать, что в волне основного типа прямоугольного волновода центр семейства линий совпадает с максимумом тока смещения.
10.4. Ввиду того, что поперечные и продольные составлявшие магнитного поля направляемой волны сдвинуты по фазе на 900, в прямоугольном волноводе, передающем волну основного типа, существуют точки, в которых вектор поляризован по кругу. Найти геометрическое место этих точек.
10.5.
Построить картину линий токов в стенках
круглого волновода для волны
![]() .
.
10.6.
Построить картину линий токов в стенках
круглого волновода для волны
![]() .
.
10.7. С помощью щели возбудить в круглом волноводе волну типа .
10.8.
В прямоугольном волноводе с помощью
штыря возбудить волну
![]() .
.
10.9.
Какие волны типа
могут распространяться в прямоугольном
волноводе размерами
![]() =
10
=
10![]() 23
мм2,
заполненном диэлектриком, если
,
=1010
Гц?
23
мм2,
заполненном диэлектриком, если
,
=1010
Гц?
10.10.
Определить длину волны типа
![]() в прямоугольном
волноводе сечением 4
3
см2
при частоте 10000 МГц. Построить картину
поля в волноводе.
в прямоугольном
волноводе сечением 4
3
см2
при частоте 10000 МГц. Построить картину
поля в волноводе.
10.11.
По прямоугольному волноводу заданных
размеров
распространяются
и
волны, причем
![]() =0,6
для обеих волн. Какая из волн переносит
большую мощность, если
=0,6
для обеих волн. Какая из волн переносит
большую мощность, если
![]() =5
В/м,
=5
В/м,
![]() =5
А/м?
=5
А/м?
10.12.
В прямоугольном волноводе размерами
распространяется
волна
![]() ,
найти выражение для токов по широкой
стенке (
,
найти выражение для токов по широкой
стенке (![]() )
волновода, прорезать в ней излучающую
щель.
)
волновода, прорезать в ней излучающую
щель.
10.13. В каких точках поперечного сечения прямоугольного волновода напряженность электрического поля всегда равна нулю для волн , ?
10.14. В прямоугольном волноводе сечением 2,3 1,0 см2 распространяется волна с максимальной напряженностью электрического поля 10 В/м. Определить максимальную величину плотности продольного электрического тока, если частота колебаний = 9375 МГц ( =3,2 см).
1
2 4
3
Рис. 10.1
10.16.
В прямоугольном волноводе с помощью
щелей возбудить колебания
,
![]() .
.
10.17. На рис. 10.1 изображен прямоугольный волновод, в котором прорезаны узкие щели. С помощью каких щелей при облучении их внешним полем можно возбудить в волноводе волну , ?
10.18. Длина волны в круглом волноводе при типе колебаний равна 4 см. Определить диаметр волновода, если рабочая частота 9375 МГц.
10.19. Напряженность поперечной составляющей магнитного поля в точке волновода с волной типа равна 100 А/м. Длина волны в волноводе, заполненном диэлектриком с =2,25, равна длине волны в воздухе. Определить напряженность электрического поля в той же точке.
10.20. Определить, какие волны типа распространяются в круглом волноводе диаметром 3 см на частоте 9000 МГц. Заполнение среда с =4.
10.21. Определить, какие типы волн могут распространяться в заполненном воздухом прямоугольном волноводе сечением =2,5 5 см2 при частоте 7,5109 Гц; найти значение критической длины волны в каждом случае. Нарисовать картины поля.
10.22.
Найти критические длины волн для
прямоугольного волновода сечением
10![]() 23
мм2.
Рассмотреть
и
волны с характеристическими числами
,
= 0, 1, 2, 3.
23
мм2.
Рассмотреть
и
волны с характеристическими числами
,
= 0, 1, 2, 3.
10.23. Определить диапазон частот, в пределах которого в круглом волноводе диаметром 4 см может распространяться только основной тип волны.
10.24. Наибольшее амплитудное значение напряженности электрического поля в прямоугольном волноводе сечением =2,5 5 см2 составляет 5 В/м, частота 7,5109 Гц, диэлектрик воздух, тип волны .
Определить амплитуду составляющей магнитного поля и поверхностной плотности тока в стенках волновода (полагая стенки сделанными из идеального проводника). Найти величину тока смещения в диэлектрике волновода.
Рис. 10.2
10.26. В квадратный волновод со стороной сечения =10 см помещена квадратная рамка, занимающая один из квадрантов поперечного сечения волновода (рис. 10.2). Определить наводимую в рамке ЭДС при волнах типов , , если амплитудное значение напряженности электрического поля у середины стенки в обоих случаях равно 5102 В/м. Стенки волновода считать идеально проводящими.
10.27. Найти фазовую скорость волны в полом металлическом волноводе, заполненном воздухом, если скорость движения энергии =1,8108 м/с.
10.28. В прямоугольном волноводе, заполненном воздухом, напряженность поля в пучности основного типа волны равна 10-3 В/м. Найти амплитуды поперечного и продольного магнитного поля, а также передаваемую мощность при =15 см, если размеры волновода =10 5 см2.
10.29. Скорость передачи энергии по прямоугольному волноводу с основным типом волны и поперечным сечением 10 3 см2 в 2 раза меньше, чем в свободном пространстве. Определить частоту генератора.
10.30. Определить затухание на единицу длины в медном волноводе сечением 2,3 1,0 см2 на частоте 10000 МГц при волне типа .
10.31. Определить потери мощности в стенках на 1м длины и коэффициент затухания прямоугольного волновода сечением 2,5 5 см2 при волне типа . Материал стенок серебро с удельной проводимостью =6,6107 См/м. Амплитудное значение продольной составляющей напряженности электрического поля в центре сечения составляет 105 В/м, частота 7,5109 Гц. Диэлектрик воздух.
10.32.
Определить величину поверхностного
сопротивления металла, если затухание
в волноводе на частоте 1000 МГц равно 1
Нп/м, длина волны в 1,2 раза больше, чем
в воздухе, а отношение поперечных
размеров волновода
![]() =4:3.
Тип волны
.
=4:3.
Тип волны
.
