3.3.5. Сверточные коды

Все рассмотренные ранее помехоустойчивые коды относились к блоковым кодам. Отличительной особенностью блоковых кодов является то, что закодированная последовательность символов представляет собой последовательность кодовых комбинаций (блоков) одинаковой длины n, каждая из которых кодировалась независимо от других. Иначе обстоит дело при использовании сверточных кодов. Дополнительные символы в таких кодах зависят от ряда предшествующих информационных символов, в результате чего передаваемая последовательность становится одним полубесконечным кодовым словом.

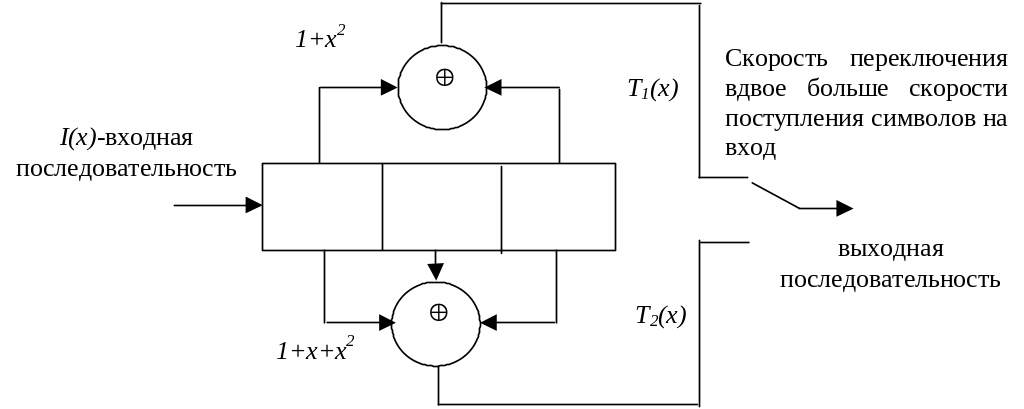
Построение сверточных кодов лучше всего рассмотреть на примере работы кодера, который любым k₀ символам входной информационной последовательности ставит во взаимно однозначное соответствие n₀ символов выходной последовательности. Простейший сверточный кодер (рис. 3.16) представляет собой регистр сдвига с k₀ разрядами, в котором символы кодовой последовательности формируются суммированием по модулю два значений с выходов некоторых разрядов регистра.

Рис. 3.16. Структура сверточного кодера

Сверточные кодеры (и коды) характеризуются скоростью кодирования R=k₀/n₀, означающей, что если в каждый момент времени (такт) k₀ символов входного кода поступают в регистр, то за это же время с выхода снимается n₀ символов выходного кода. Для данного примера R=k₀/n₀ = 1/2, т.е. поступление каждого символа на вход приводит к появлению двух символов на выходе. Другой важнейшей характеристикой является длина кодового ограничения или просто кодовое ограничение, равное числу разрядов регистра, в связи с чем эту характеристику называют иногда памятью кода. Величина n_A = mn₀ называется полной длиной кодового ограничения. Величина полного кодового ограничения характеризует протяженность корреляционных связей в кодированной последовательности для одного информационного символа. Если на вход кодера подавать различные информационные последовательности и каждый раз на длине n_A выходной последовательности фиксировать ее вес, то минимальный зафиксированный вес даст значение т.н. свободного кодового расстояния d_СВ.

Связи между разрядами регистра и сумматорами по модулю два удобно описывать порождающими полиномами. Для приведенной схемы и . При таком представлении символы на входе кодера могут быть получены путем умножения входной последовательности на порождающие полиномы, т.е. и . Рассматриваемый в примере сверточный код является несистематическим, поскольку ни , ни не совпадают с входной последовательностью . Для получения систематического сверточного кода необходимо было бы положить или , или , т.е. убрать один из сумматоров, чтобы информационная входная последовательность стала частью выходной.

Рассматриваемый сверточный кодер под воздействием нулевой входной последовательности будет выдавать нулевую выходную последовательность. Если, например, подать в кодер один символ 1, за которой последуют нули, то выходная последовательность будет иметь вид

	1 такт	2 такт	3 такт	4 такт
Сост. регистра	100	010	001	000
Т1	1	0	1	0
Т2	1	1	1	0

Таким образом, входная последовательность 1000 . . . порождает выходную последовательность 1101110000 . . . .

Порождающая матрица кода может быть построена аналогично ранее рассмотренным, но в виде полубесконечной матрицы

.

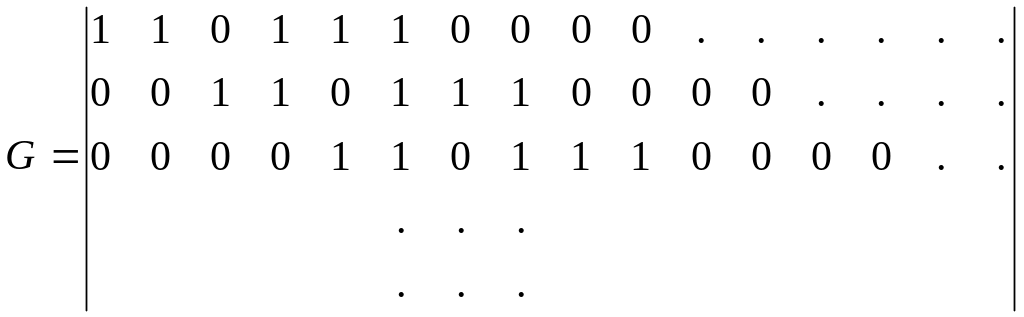Выходная последовательность, соответствующая произвольной входной последовательности может быть получена путем суммирования по модулю два соответствующих сочетаний строк этой матрицы.

Таким образом, сверточный код, формируемый этим кодером, имеет следующие параметры:

-скорость кодирования R=1/2;

-кодовое ограничение m=3;

-полное кодовое ограничение n_A=6;

-свободное кодовое расстояние d_СВ=5.

Другой способ описания связей между входной и выходной последовательностями сверточного кодера состоит в использовании кодового дерева, в котором каждая вершина соответствует очередному входному символу, а на ребре, ведущем к этой вершине, записывается соответствующая совокупность входных символов. Таким образом, каждая входная последовательность задает некоторый путь на дереве, а совокупности символов, соответствующие ребрам, составляющим этот путь, образуют выходную последовательность. Ясно, что при росте длины входной последовательности число возможных путей растет экспоненциально, так что использование такого дерева не очень удобно.

Более удобным является представление в виде т. н. решетчатого графа. Решетчатым называют граф, узлы которого находятся в узлах прямоугольной координатной сетки, т.е. образуют строки и столбцы. Граф полубесконечен справа, т.е. число столбцов полубесконечно. Число узлов в каждом столбце, т.е. число строк конечно и равно , где m - длина кодового ограничения. Конфигурация ребер, соединяющих узлы каждого столбца с узлами столбца справа, одинакова для всего графа. На основании сказанного построим решетчатый граф (рис. 3.17) для кодера, приведенного ранее, условившись, что из двух ребер, выходящих из каждого узла, верхнее соответствует входному символу 0, нижнее – 1.

Рис. 3.17. Решетчатый граф

Продемонстрируем процесс кодирования с помощью решетчатого графа, например, кодируя входную комбинацию =101100 . . ., т.е. выходная комбинация, найденная по графу (жирные линии) будет 1101001010, что можно проверить, воспользовавшись построенной ранее образующей матрицей и сложив по модулю два 1, 3 и 4 ее строки

.

Задачу декодирования сверточного кода можно рассматривать как задачу нахождения пути на решетчатом графе с помощью некоторых правил декодирования. Как и в случае декодирования блоковых кодов по максимуму правдоподобия целесообразными оказываются попытки выбрать правильный путь, который лучше всего согласуется с принятой последовательностью, т.е. попытки минимизировать вероятность ошибки последовательности. Поскольку с ростом длины последовательности число путей растет экспоненциально, то на первый взгляд задача построения оценки последовательности по максимуму правдоподобия для сверточного кода кажется безнадежной. Однако, метод построения такой оценки достаточно легко найти, пытаясь непосредственно вычислить метрику для каждого пути на решетке. Вначале число путей действительно растет экспоненциально с ростом длины последовательности. Однако, вскоре появляется возможность исключить из рассмотрения такое число путей в каждой вершине, которое в точности уравновешивает число вновь появившихся путей. Таким образом, оказывается возможным иметь сравнительно небольшой список путей, который всегда будет содержать наиболее правдоподобный путь. Эта итеративная процедура декодирования называется алгоритмом Витерби. Проще всего рассмотреть функционирование алгоритма Витерби на примере уже приведенной решетчатой диаграммы для кода с R = 1/2 и m=3. Заметим, что в ней имеется ровно по два пути, ведущих в каждую вершину уровня 4. Поскольку, начиная с этого уровня, соответствующие пути совпадают, декодер максимального правдоподобия может без потери общности принимать решение соответствующее этой вершине. После того, как это сделано, аналогичная процедура может быть применена к следующему уровню и т.д. Именно таким образом работает алгоритм Витерби. Согласно ему на каждом уровне сравниваются два пути, входящие в каждую вершину, и сохраняется лишь тот из них, метрика которого лучше. В качестве метрики может служить расстояние Хэмминга между принятой последовательностью и кодовыми словами, считываемыми с ребер решетки. Другой путь с худшей метрикой исключается из рассмотрения. Оставшиеся пути называются выжившими. Для рассматриваемого кода с m=3 в каждый момент будет сохраняться не более 4 выживших путей.

Для упрощения демонстрации работы алгоритма Витерби положим, что передавалась нулевая последовательность 00000000. . . , а принятой оказалась последовательность с одной ошибкой 10000000. . . .

Тогда работа алгоритма может быть описана следующими фрагментами:

1) принимаемый кадр n0 символов – 10. Декодер выберет оба пути и определит метрику каждого из них – цифра над узлом;

2) принимаемый кадр 00;

3) принимаемый кадр 00;

4) принимаемый кадр 00;

5) принимаемый кадр 00;

6) принимаемый кадр 00.

Можно заметить, что 5 и 6 кадры аналогичны, т.е. процесс будет повторяться при приеме каждого очередного кадра, поскольку больше ошибок в принятой комбинации нет. Можно также заметить, что метрика нулевого пути лучше всех остальных. Из примера ясно, что выживающие пути могут отличаться друг от друга в течение долгого времени. Однако в данном примере при приеме 6 кадра первые 4 ребра всех путей совпадают. В этот момент согласно алгоритму Витерби принимается решение о переданных символах, т.к. выжившие пути приходят из одной вершины, т.е. соответствуют оному информационному символу, т.е. по 6 кадру можно с максимальным правдоподобием предположить, что передавалась последовательность 00000000, соответствующая декодированной последовательности 0000.

Глубина, на которой осуществляется принятие решения, не может быть вычислена заранее, она является случайной величиной, зависящей от серьезности происходящих в канале ошибок. Поэтому при практической реализации декодера Витерби устанавливается фиксированная глубина декодирования или ширина окна декодирования b. Каждый раз при приеме нового кадра декодер выдает выходящий за пределы окна самый старый символ одного из выживших путей. Такой процесс декодирования кадров продолжается бесконечно. Если b выбрано достаточно большим, то почти всегда при декодировании может быть принято однозначное решение. Если для данного канала с известными параметрами помех код выбран надлежащим образом, то это решение с большой вероятностью будет правильным. Этому, однако, может помешать несколько обстоятельств. Не все выжившие пути могут проходить через один и тот же узел. Возникает неопределенность, и процесс декодирования нарушается. Декодер может разрешить неопределенность, используя любое произвольное правило. Другая возможность состоит в том, что декодер не принимает решения, а отмечает этот участок последовательности, как сегмент кодового слова, который невозможно исправить. В этом случае декодер становится неполным декодером. Иногда декодер принимает однозначное, но ошибочное решение. Оно обязательно сопровождается последующими дополнительными ошибочными решениями, но декодер через некоторое время обнаружит это.

Основные трудности при реализации алгоритма Витерби возникают из-за того, что сложность декодера экспоненциально растет с ростом длины кодового ограничения m. Поэтому значения m должны быть сравнительно небольшими m <10 или должны использоваться другие алгоритмы декодирования. Для того, чтобы ослабить влияние больших длин кодового ограничения, была разработана стратегия декодирования, игнорирующая маловероятные пути по решетке, как только они становятся маловероятными. Все такие стратегии поиска наиболее вероятного пути на решетке известны по общим названием последовательного декодирования.

В отличие от декодера Витерби, который производит продолжение и обновление метрики всех путей, которые могут оказаться наилучшими, последовательный декодер в каждый момент времени продолжает лишь один путь, который имеет вид наиболее вероятного. На каждом уровне последовательный декодер находится в одном узле, смотрит на следующий кадр и выбирает ребро, ближайшее к принятому кадру, переходя по этому ребру в узел на следующем уровне. Если нет ошибок, процедура работает отлично, однако при наличии ошибок декодер может выбрать неправильный путь. Если декодер продолжает следовать по ложному пути, он обнаруживает, что происходит слишком много ошибок. Но это ошибки декодера, а не канала. Последовательный декодер вернется назад на несколько кадров и начнет исследовать альтернативные пути до тех пор, пока не найдется правдоподобный путь, затем он будет следовать вдоль этого альтернативного пути. Разработаны различные подробные алгоритмы реализации этих процедур. Наиболее популярным из них является алгоритм Фано.

В этом алгоритме требуется знать вероятность p появления ошибочного символа в канале. Пока декодер следует по правильному пути вероятное число ошибок в первых l кадрах приблизительно равно p ln₀. Декодер допускает несколько большее число ошибок, но если оно намного больше, то декодер сделает вывод о том, что он находится на ложном пути.

Для декодера выбирается некоторый параметр p¹, такой, что p<p¹<1/2 и определяется перекошенное расстояние , где - расстояние Хэмминга между принятым словом и текущим путем по решетке. Для правильного пути  , в связи с чем и возрастает по мере движения. До тех пор, пока возрастает, декодер продолжает движение вперед по решетке. Если начинает уменьшаться, то декодер заключает, что в некотором узле он выбрал неправильное решение и возвращается по решетке, проверяя другие пути. Для того, чтобы решить, когда уменьшится на недопустимую величину, декодер пользуется переменным порогом Т, который может быть уменьшен или увеличен на величину , называемую приращением порога. На каждом шаге декодер решает, что делать, основываясь на сравнении перекошенного расстояния и текущего значения порога Т. До тех пор, пока остается выше порога, декодер продолжает двигаться вперед и повышать порог, подсуммируя , так, чтобы он оставался близким к . Если опускается ниже порога, то декодер проверяет альтернативные ребра этого кадра, пытаясь найти то ребро, которое находится выше порога. Если он не может этого сделать, то возвращается назад. Алгоритм заставляет декодер двигаться назад до тех пор, пока он не найдет альтернативный путь, который находится над текущим значением порога, или, если это невозможно, не найдет узел, в котором был установлен текущий порог и понизит его на . Затем декодер снова начнет двигаться вперед с уже пониженным порогом и порог не будет повышаться до тех пор, пока декодер не придет в новый, ранее не исследованный узел решетки.

Таким образом, каждый раз, когда декодер, двигаясь вперед, посещает ранее исследованный узел, он имеет меньший порог. Декодер никогда не посетит один и тот же узел дважды с одним и тем же порогом. Следовательно, он может посещать любой узел конечное число раз. Это поведение гарантирует декодер от зацикливания. Декодер продолжает обработку данных, проводя правильное или неправильное декодирование.

Основная сложность при реализации последовательного декодера состоит в том, что число вычислительных операций, необходимых для продвижения в следующую вершину кодового дерева, является случайной величиной. Наиболее существенным следствием непостоянства объема вычислений, требуемых для декодирования одного символа, является необходимость в наличии большой емкости памяти для буферизации поступающих и обрабатываемых данных. Использование в последовательном декодере буферной памяти любого, но конечного объема, приводит к ненулевой вероятности его переполнения. Исходя их этой характеристики, находится т.н. вычислительная скорость декодера R₀ . Если скорость кода R>R₀ , то в любом последовательном декодере будут возникать серьезные вычислительные трудности, связанные с частыми переполнениями буфера.

Для декодирования сверточных кодов могут использоваться и методы синдромного декодирования, среди которых наиболее часто употребляемыми являются метод порогового декодирования и метод табличного поиска. Следует отметить, что синдромное декодирование в преобладающем большинстве случаев используется только для систематических сверточных кодов, т.е. таких, у которых кодовая последовательность содержит явно выделяемые информационные и контрольные символы.

Пороговое декодирование сверточных кодов основано на тех же принципах, что и мажоритарное декодирование блоковых кодов. Декодер, реализующий этот алгоритм, по принятой информационной последовательности вычислят проверочные символы. Для этого декодер содержит копию кодера. Далее полученные с помощью этой копии проверочные символы складываются по модулю два с принимаемой проверочной последовательностью, в результате чего формируется синдромная последовательность, записываемая в регистр сдвига. С помощью линейного преобразования синдрома формируется система ортогональных проверок. Если результаты этих проверок подать на входы пороговой или решающей схемы, то на ее выходе будет формироваться оценка ошибочного символа. Суммируя его по модулю два с соответствующим информационным символом, который хранится в копии кодера, можно исправить ошибку. При этом выходной символ пороговой схемы по цепи обратной связи подается еще и на схему вычисления синдрома и корректирует его, устраняя влияние вычисленной ошибки на последующие символы. Такая процедура порогового декодирования называется декодированием с обратной связью.

Среди сверточных кодов, допускающих пороговое декодирование, самыми простыми являются т.н. самоортогональные коды. Декодирование самоортогональных кодов осуществляется крайне просто. Это связано с тем, что при декодировании нет необходимости проводить линейное преобразование символов синдрома для получения ортогональных проверок, поскольку в качестве таковых используются непосредственно символы синдрома.

Еще одним классом сверточных кодов, допускающих пороговое декодирование, являются ортогонализируемые коды. Ортогонализируемый код – это код, который допускает для каждого информационного символа построение системы ортогональных проверок, являющихся линейными комбинациями символов синдрома. Параметры этих кодов можно найти там же.

Если шумы в канале не выходят за пределы допустимых, то исправление ошибок осуществляется правильно. Если шумы превышают корректирующие способности кода, то могут возникнуть естественные ошибки декодирования. Однако, поскольку декодер содержит цепь обратной связи, то при возникновении ошибки декодирования по неправильной оценке значений ошибок осуществляется неправильная коррекция синдрома, что может привести к новой ошибке декодирования. Это явление характерно для сверточных кодов и известно под названием распространения ошибок.

Одним из методов борьбы с распространением ошибок является т.н. метод дефинитного декодирования. При этом декодировании исправления синдрома не производится, т.е. обратная связь отсутствует. Однако при таком декодировании и достаточно больших кодовых ограничениях корректирующие способности кодов обычно оказываются хуже, чем при декодировании с обратной связью.

Отличие метода табличного поиска от метода порогового декодирования с обратной связью состоит только в том, что в качестве решающего устройства используется ПЗУ с произвольным доступом, из которого по адресу, равному текущему синдрому, выбирается наиболее вероятная комбинация ошибок, записанная в него на этапе проектирования системы.

Контрольные

вопросы к

лекции 16

16-1. Как определяется скорость кодирования сверточного кода?

16-2. Чем определяется память сверточного кода?

16-3. Что называется полной длиной кодового ограничения сверточного кода?

16-4. Что характеризует полная длина кодового ограничения сверточного кода?

16-5. Как определяется свободное кодовое расстояние сверточного кода?

16-6. Какой граф называется решетчатым?

16-7. Чем определяется число узлов в каждом столбце решетчатого графа, описывающего сверточный кодер?

16-8. Что служит критерием выживания путей на решетчатом графе при использовании для декодирования сверточного кода алгоритма Витерби?

16-9. Чем принципиально отличается алгоритм Фано от алгоритма Витерби?

16-10. Как определяется перекошенное кодовое расстояние при использовании алгоритма Фано для декодирования сверточного кода?

16-11. За счет чего обеспечивается отсутствие зацикливания декодера Фано?

16-12. Для декодирования каких сверточных кодов может быть использовано синдромное декодирование?

16-13. Чем вызвано явление распространения ошибок в синдромном декодере сверточного кода с обратной связью?

16-14. В чем состоит особенность дефинитного декодирования сверточных кодов?

16-15. Что используется в качестве решающего устройства при использовании для декодирования сверточных кодов метода табличного поиска?

Лекция 17

Каскадные

коды.

Эффективность

помехоустойчивого

кодирования