Раздел 2. Основные уравнения электромагнитного поля

Тема 1. Основные уравнения электромагнитного поля

Вопрос 1. Основные положения теории электромагнитного поля

Математическую основу теории электромагнитного поля составляют уравнения Мак­свелла, традиционно, в технических приложениях, трактуемые как обобщения ряда эмпири­ческих закономерностей. Так первое уравнение Максвелла является обобщением закона пол­ного тока Ампера (теоремы о циркуляции вектора напряженности магнитного поля) и фор­мулируется следующим образом:

(2.1)

Интеграл в левой части (2.1) имеет смысл циркуляции вектора напряженности магнитного поля по произвольному замкнутому контуру, охватывающему линии тока. В правой части записан так называемый полный ток, являющийся алгебраической суммой величин то­ков проводимости и смещения

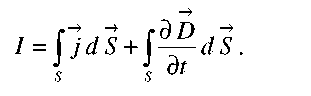
(2.2)

Второе слагаемое в правой части (2.2) пред­ставляет собой величину тока смещения, опреде­ляемую как

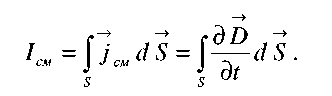(2.3)

Таким образом, плотность тока смещения определяется скоростью изменения вектора электрического смещения во времени. Линии вектора плотности тока смещения замыкают линии полного тока в областях, где отсутствует электропроводность.

Взаимное расположение линий тока и контура Г показано на рис.1. Поверхность S, че­рез которую вычисляется поток линий плотности тока в (2.1) и (2.2), опирается на контур Г.

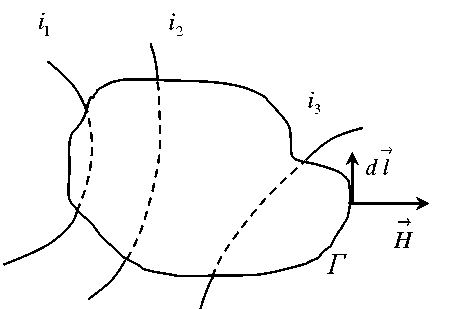
Рис.2.1.

Запись вида (2.2) называют интегральной формой первого уравнения Максвелла. Ис­пользование теоремы о том, что циркуляция любого вектора равна потоку ротора этого век­тора, через поверхность, опирающуюся на контур, по которому вычисляется циркуляция, из­вестной под названием теоремы Стокса, позволяет получить дифференциальную форму первого уравнения Максвелла:

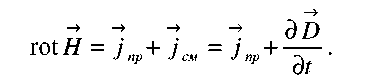
(2.4)

Второе уравнение Максвелла, как правило, рассматривают как обобщенный закон электромагнитной индукции Фарадея – Ленца

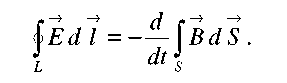
(2.5)

Циркуляция вектора напряженности электрического поля в левой части (2.5) имеет смысл ЭДС, наводимой переменным магнитным потоком в контуре L. При этом предполага­ется, что контур L пронизывается линиями магнитного поля. Соотношения между контуром и поверхностью, по которой вычисляется интеграл в правой части аналогичны предыдущему случаю. Интеграл в правой части представляет собой ни что иное, как скорость изменения во времени переменного магнитного потока, охватываемого контуром L.

Применение теоремы Стокса позволяет записать второе уравнение Максвелла в диф­ференциальной форме следующим образом:

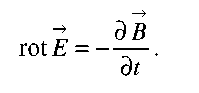(2.6)

Сопоставление (2.4) и (2.6) позволяет сделать вывод о сходности структур первого и второго уравнений.

Отсутствие в правой части (2.6) слагаемого, аналогичного плотности тока проводимо­сти, обусловлено тем обстоятельством, что носителей магнитного заряда и магнитных токов в природе не существует.

Третье уравнение Максвелла представляет собой закон Гаусса, распространенный на общий случай переменных во времени и пространстве зарядов:

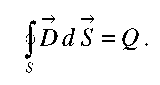
(2.7)

Интеграл в левой части (2.7) представляет собой поток вектора электрического сме­щения через произвольную поверхность. Член в правой части имеет смысл полного заряда, заключенного в этой поверхности:

(2.7)

где V - объём, ограниченный поверхностью S, ρ - объёмная плотность электрического заря­да, определяемая следующим образом:

(2.8)

Применение теоремы о равенстве потока вектора через замкнутую поверхность объ­емному интегралу от дивергенции, взятому по объему, ограниченному этой поверхностью, известной под названием теоремы Остроградского, можно легко получить дифференциаль­ную форму третьего уравнений Максвелла:

(2.9)

Четвертое уравнение Максвелла по структуре аналогично третьему с нулевой правой частью, что опять-таки является следствием отсутствия в природе автономных носителей магнитного заряда:

(2.10)

Сравнительный анализ (2.9) и (2.10) говорит о том, что электрическое поле может существовать как в потенциальной (линии вектора E разомкнуты, начинаются и заканчиваются на зарядах), так и в соленоидальной (линии вектора E замкнуты) формах. Причем, потенци­альная форма электрического поля создается неизменными во времени электрическими заря­дами, а соленоидальная – переменными. Линии же магнитного поля всегда замкнуты.

Система уравнений Максвелла традиционно дополняется дифференциальными фор­мулировками закона Ома, закона сохранения электрического заряда и уравнения непрерыв­ности линий электрического тока.

Закон сохранения электрического заряда записывается следующим образом:

или, с учетом (2.8, 2.9):

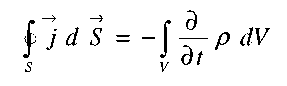
(2.11)

Выражение (19) представляет собой интегральную форму закона сохранения электри­ческого заряда. Дифференциальная форма может быть получена при помощи теоремы Ост­роградского:

(2.12)

Закон непрерывности линий полного тока получается после подстановки в (2.12) третьего уравнения Максвелла:

(2.13)

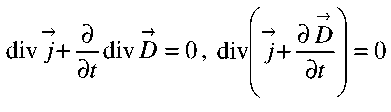
или, учитывая физический смысл производной в левой части (2.13), можно записать:

(2.14)

Иными словами, линии полного тока не имеют ни источников, ни стоков, то есть все­гда замкнуты.

Под законом Ома в дифференциальной форме понимают выражение (2.11).