Вопрос 2 Диэлектрический волновод круглого сечения. Типы волн в диэлектрическом волноводе.

Круглый диэлектрический волновод представляет собой стер­жень круглого поперечного сечения радиусом а с проницаемостями и помещенный в безграничную среду с па­раметрами и (рис. 5.12). Для вывода дисперсионного уравнения этого волновода запишем решение уравнения внутри стержня :

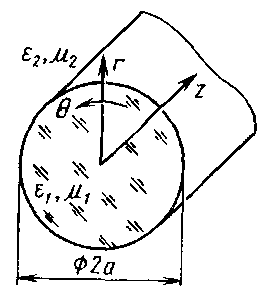
Рис. 5.12.

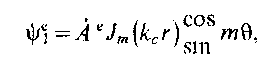(5.49)

где - функция, связанная с электрическим вектором Герца.

Т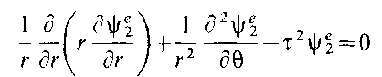 ак как в окружающей среде поперечное волновое число мнимое, уравнение для этой области приобретает вид

(5.50)

Р ешив его методом разделения переменных, получим

(5.51)

где - модифицированные функции Бесселя первого и второго рода порядка т. Поскольку поле на бесконечности должно отсутствовать, постоянную интегрирования В^е принимаем равной нулю. Таким образом, функция определена:

(5.52)

Так как при т>0 на границе раздела , в общем случае в круглом ДВ распространяются гибридные волны. Поэтому наряду с (5.49) и (5.52) необходимо иметь выражения для функции связанной с маг­нитным вектором Герца. Запишем их в виде

(5.53)

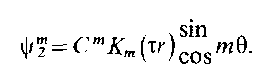
З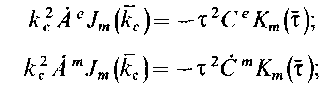 начения функций на границе раздела

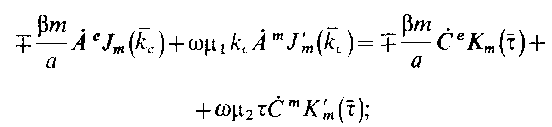
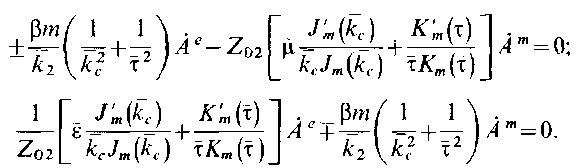
Для упрощения дальнейших вычислений введем функции

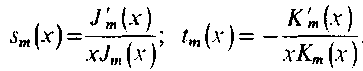
Используя эти обозначения, приравняем определитель системы уравнений нулю, что является условием существования нетриви­альных решений:

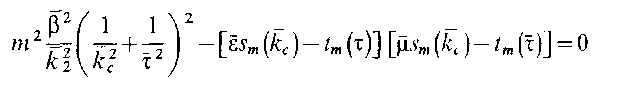
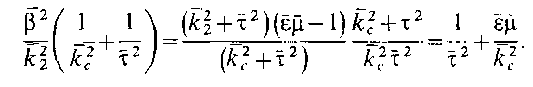
Получим дисперсионное уравнение для круглого ДВ

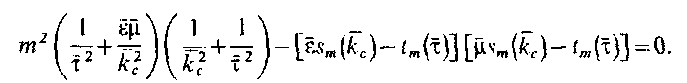(5.54)

Дисперсионные кривые, построенные по уравнению (рис. 5.54) для различных m, показаны на рис. 5.13. Эпюра силовых линий электромагнитного поля волны ти­па ЕН₁₀ в круглом ДВ: _______линии вектора Е; --------- линии вектора Н (рис. 5.14). Заметим, что при отсутствии вариаций поля по азимуту (m = 0) Е- и Н-волны могут распространять­ся в волноводе независимо друг от друга. Дисперсионное уравнение разделяется при этом на два. Приравняв нулю первую квадратную скобку в (5.54), получим уравнение для волн типа Е_0n ( ). Первый индекс этого обозначения указывает число m вариаций поля по азимуту, второй равен числу нулей функции на промежутке (0, а) при Q = const. Приравняв нулю вторую квадратную скобку (5.54), получим дисперсионное уравнение для волн типов Н_0n.

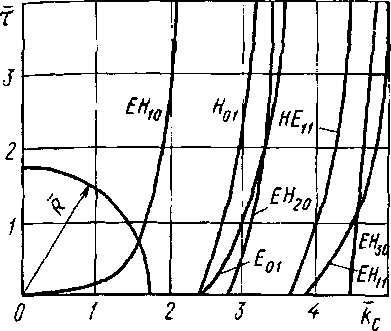
Рис. 5.13.

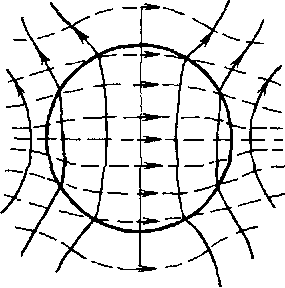
Рис. 5.14.

При наличии вариаций поля по азимуту ( ) в круглом ДВ распространяются гибридные волны. При этом каждому значению индекса m соответствуют два решения дисперсионного уравнения (две дисперсионные кривые), отличающиеся отношени­ем коэффициентов и . Действительно,

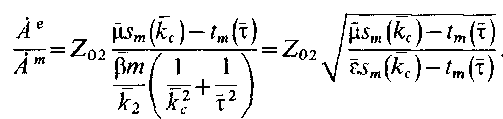(5.55)

Э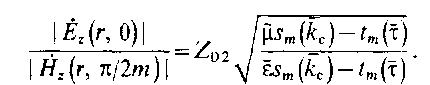 то отношение равно отношению максимальных значений амплитуд продольных со­ставляющих напряженностей электрического и магнитного полей волны на данном радиусе r. Используя (5.54), найдем

(5.56)

Численный анализ показывает, что для одного из решений значение квадратного корня меньше, а для другого – больше единицы. В первом случае отношение меньше, чем отношение поперечных составляющих электрического и магнит­ного полей в плоской волне, распространяющейся во второй среде. Такие волны обозначаются НЕ_mn, так как магнитное поле в них «больше» электрического. Другое решение соответствует волнам типа ЕН_mn.

Основным типом волны в круглом ДВ является гибридная волна ЕН₁₀, критическая частота которой равна нулю. Эпюра силовых линий электромагнитного поля этой волны показана на рис. 5.14.